Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T13:12:20.611Z Has data issue: false hasContentIssue false
  • English
  • Français

On the role of return to isotropy in wall-bounded turbulent flows with buoyancy

Published online by Cambridge University Press:  28 September 2018

Elie Bou-Zeid Open the ORCID record for Elie Bou-Zeid [Opens in a new window] ,
Xiang Gao ,
Cedrick Ansorge  and
Gabriel G. Katul
Elie Bou-Zeid*
Affiliation:
Department of Civil and Environmental Engineering, Princeton University, Princeton, NJ 08544, USA
Xiang Gao
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Cedrick Ansorge
Affiliation:
Institute for Geophysics and Meteorology, University of Cologne, 50969 Cologne, Germany
Gabriel G. Katul
Affiliation:
Nicholas School of the Environment, Box 80328, Duke University, Durham, NC 27708, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

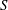High Reynolds number wall-bounded turbulent flows subject to buoyancy forces are fraught with complex dynamics originating from the interplay between shear generation of turbulence ($S$) and its production or destruction by density gradients (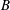$B$). For horizontal walls, 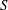$S$ augments the energy budget of the streamwise fluctuations, while 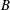$B$ influences the energy contained in the vertical fluctuations. Yet, return to isotropy remains a tendency of such flows where pressure–strain interaction redistributes turbulent energy among all three velocity components and thus limits, but cannot fully eliminate, the anisotropy of the velocity fluctuations. A reduced model of this energy redistribution in the inertial (logarithmic) sublayer, with no tuneable constants, is introduced and tested against large eddy and direct numerical simulations under both stable (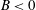$B<0$) and unstable (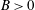$B>0$) conditions. The model links key transitions in turbulence statistics with flux Richardson number (at 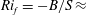$Ri_{f}=-B/S\approx$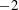$-2$, 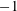$-1$ and 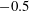$-0.5$) to shifts in the direction of energy redistribution. Furthermore, when coupled to a linear Rotta-type closure, an extended version of the model can predict individual variance components, as well as the degree of turbulence anisotropy. The extended model indicates a regime transition under stable conditions when 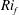$Ri_{f}$ approaches 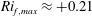$Ri_{f,max}\approx +0.21$. Buoyant destruction $B$ increases with increasing stabilizing density gradients when 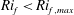$Ri_{f}<Ri_{f,max}$, while at 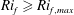$Ri_{f}\geqslant Ri_{f,max}$ limitations on the redistribution into the vertical component throttle the highest attainable rate of buoyant destruction, explaining the ‘self-preservation’ of turbulence at large positive gradient Richardson numbers. Despite adopting a ‘framework of maximum simplicity’, the model results in novel and insightful findings on how the interacting roles of energy redistribution and buoyancy modulate the variance budgets and the energy exchange among the components.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Convection: Buoyant boundary layers Turbulent Flows: Stratified turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 61 - 78
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, J. C., De Moor, G., Lacarrère, P. & du Vachat, R. 1978 Modeling the 24-hour evolution of the mean and turbulent structures of the planetary boundary layer. J. Atmos. Sci. 35 (10), 1861–1883.Google Scholar
Ansorge, C. & Mellado, J. P. 2014 Global intermittency and collapsing turbulence in the stratified planetary boundary layer. Boundary-Layer Meteorol. 153 (1), 89–116.Google Scholar
Ansorge, C. & Mellado, J. P. 2016 Analyses of external and global intermittency in the logarithmic layer of Ekman flow. J. Fluid Mech. 805, 611–635.Google Scholar
Bou-Zeid, E., Higgins, C., Huwald, H., Meneveau, C. & Parlange, M. B. 2010 Field study of the dynamics and modelling of subgrid-scale turbulence in a stable atmospheric surface layer over a glacier. J. Fluid Mech. 665, 480–515.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2004 Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res. 40 (2), W02505.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 25105.Google Scholar
Briard, A., Gomez, T., Mons, V. & Sagaut, P. 2016 Decay and growth laws in homogeneous shear turbulence. J. Turbul. 17 (7), 699–726.Google Scholar
Brugger, P., Katul, G. G., De Roo, F., Kröniger, K., Rotenberg, E., Rohatyn, S. & Mauder, M. 2018 Scalewise invariant analysis of the anisotropic Reynolds stress tensor for atmospheric surface layer and canopy sublayer turbulent flows. Phys. Rev. Fluids 3 (5), 054608.Google Scholar
Canuto, V. M., Howard, A., Cheng, Y. & Dubovikov, M. S. 2001 Ocean turbulence. Part I: one-point closure model – momentum and heat vertical diffusivities. J. Phys. Oceanogr. 31 (6), 1413–1426.Google Scholar
Chauhan, K., Hutchins, N., Monty, J. & Marusic, I. 2012 Structure inclination angles in the convective atmospheric surface layer. Boundary-Layer Meteorol. 147 (1), 41–50.Google Scholar
Dougherty, J. P. 1961 The anisotropy of turbulence at the meteor level. J. Atmos. Terr. Phys. 21 (2), 210–213.Google Scholar
Fernando, H. J. S. & Weil, J. C. 2010 Whither the stable boundary layer? Bull. Am. Meteorol. Soc. 91 (11), 1475–1484.Google Scholar
Foken, T. 2006 50 years of the Monin–Obukhov similarity theory. Boundary-Layer Meteorol. 119 (3), 431–447.Google Scholar
Garcia, J. R. & Mellado, J. P. 2014 The two-layer structure of the entrainment zone in the convective boundary layer. J. Atmos. Sci. 71 (6), 1935–1955.Google Scholar
Gerz, T., Schumann, U. & Elghobashi, S. 1989 Direct numerical-simulation of stratified homogeneous turbulent shear flows. J. Fluid Mech. 200, 563–594.Google Scholar
Ghannam, K., Katul, G. G., Bou-Zeid, E., Gerken, T. & Chamecki, M. 2018 Scaling and similarity of the anisotropic coherent eddies in near-surface atmospheric turbulence. J. Atmos. Sci. 75 (3), 943–964.Google Scholar
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S. & Persson, P. O. G. 2013 The critical Richardson number and limits of applicability of local similarity theory in the stable boundary layer. Boundary-Layer Meteorol. 147 (1), 51–82.Google Scholar
Grachev, A. A., Andreas, E. L., Fairall, C. W., Guest, P. S. & Persson, P. O. G. 2015 Similarity theory based on the Dougherty–Ozmidov length scale. Q. J. R. Meteorol. Soc. 141 (690), 1845–1856.Google Scholar
Heinze, R., Mironov, D. & Raasch, S. 2016 Analysis of pressure-strain and pressure gradient-scalar covariances in cloud-topped boundary layers: a large-eddy simulation study. J. Adv. Model. Earth Syst. 8 (1), 3–30.Google Scholar
Holt, S. E., Koseff, J. R. & Ferziger, J. H. 1992 A numerical study of the evolution and structure of homogeneous stably stratified sheared turbulence. J. Fluid Mech. 237, 499–539.Google Scholar
Huang, J. & Bou-Zeid, E. 2013 Turbulence and vertical fluxes in the stable atmospheric boundary layer. Part I: a large-eddy simulation study. J. Atmos. Sci. 70 (6), 1513–1527.Google Scholar
van Hooijdonk, I. G. S., Clercx, H. J. H., Ansorge, C., Moene, A. F. & van de Wiel, B. J. H. 2018 Parameters for the collapse of turbulence in the stratified plane Couette flow. J. Atmos. Sci. 75, 3211–3231.Google Scholar
Isaza, J. C. & Collins, L. R. 2009 On the asymptotic behaviour of large-scale turbulence in homogeneous shear flow. J. Fluid Mech. 637, 213–239.Google Scholar
Jacobitz, F. G., Sarkar, S. & Vanatta, C. W. 1997 Direct numerical simulations of the turbulence evolution in a uniformly sheared and stably stratified flow. J. Fluid Mech. 342, 231–261.Google Scholar
Kader, B. A. & Yaglom, A. M. 1990 Mean fields and fluctuation moments in unstably stratified turbulent boundary-layers. J. Fluid Mech. 212, 637–662.Google Scholar
Karimpour, F. & Venayagamoorthy, S. K. 2015 On turbulent mixing in stably stratified wall-bounded flows. Phys. Fluids 27 (4), 046603.Google Scholar
Katul, G. G., Konings, A. G. & Porporato, A. 2011 Mean velocity profile in a sheared and thermally stratified atmospheric boundary layer. Phys. Rev. Lett. 107 (26), 268502.Google Scholar
Katul, G. G., Porporato, A., Manes, C. & Meneveau, C. 2013 Co-spectrum and mean velocity in turbulent boundary layers. Phys. Fluids 25 (9), 91702.Google Scholar
Katul, G. G., Porporato, A., Shah, S. & Bou-Zeid, E. 2014 Two phenomenological constants explain similarity laws in stably stratified turbulence. Phys. Rev. E 89 (2), 023007.Google Scholar
Keitzl, T., Mellado, J. P. & Notz, D. 2016 Impact of thermally driven turbulence on the bottom melting of ice. J. Phys. Oceanogr. 46 (4), 1171–1187.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (3), 537–566.Google Scholar
Li, D. & Bou-Zeid, E. 2011 Coherent structures and the dissimilarity of turbulent transport of momentum and scalars in the unstable atmospheric surface layer. Boundary-Layer Meteorol. 140 (2), 243–262.Google Scholar
Li, D., Katul, G. G. & Liu, H. 2018 Intrinsic constraints on asymmetric turbulent transport of scalars within the constant flux layer of the lower atmosphere. Geophys. Res. Lett. 45 (4), 2022–2030.Google Scholar
Li, D., Salesky, S. T. & Banerjee, T. 2016 Connections between the Ozmidov scale and mean velocity profile in stably stratified atmospheric surface layers. J. Fluid Mech. 797, R3.Google Scholar
Mahrt, L. 2014 Stably stratified atmospheric boundary layers. Annu. Rev. Fluid Mech. 46 (1), 23–45.Google Scholar
McColl, K. A., Katul, G. G., Gentine, P. & Entekhabi, D. 2016 Mean-velocity profile of smooth channel flow explained by a cospectral budget model with wall-blockage. Phys. Fluids 28 (3), 035107.Google Scholar
Mellado, J. P. 2012 Direct numerical simulation of free convection over a heated plate. J. Fluid Mech. 712, 418–450.Google Scholar
Mellor, G. L. & Yamada, T. 1982 Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 20 (4), 851–875.Google Scholar
Miles, J. W. & Howard, L. N. 1964 Note on a heterogeneous shear flow. J. Fluid Mech. 20 (2), 331–336.Google Scholar
Moeng, C. 1984 A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41 (13), 2052–2062.Google Scholar
Momen, M. & Bou-Zeid, E. 2017 Mean and turbulence dynamics in unsteady Ekman boundary layers. J. Fluid Mech. 816, 209–242.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the ground layer of the atmosphere. Akad. Nauk. SSSR. Geofiz. Inst. Trudy 151, 163–187.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pumir, A. 1996 Turbulence in homogeneous shear flows. Phys. Fluids 8 (11), 3112–3127.Google Scholar
Salesky, S. T., Chamecki, M. & Bou-Zeid, E. 2017 On the nature of the transition between roll and cellular organization in the convective boundary layer. Boundary-Layer Meteorol. 163 (1), 41–68.Google Scholar
Salesky, S. T., Chamecki, M. & Dias, N. L. 2012 Estimating the random error in eddy-covariance based fluxes and other turbulence statistics: the filtering method. Boundary-Layer Meteorol. 144 (1), 113–135.Google Scholar
Shah, S. K. & Bou-Zeid, E. 2014a Direct numerical simulations of turbulent Ekman layers with increasing static stability: modifications to the bulk structure and second-order statistics. J. Fluid Mech. 760, 494–539.Google Scholar
Shah, S. & Bou-Zeid, E. 2014b Very-large-scale motions in the atmospheric boundary layer educed by snapshot proper orthogonal decomposition. Boundary-Layer Meteorol. 153 (3), 355–387.Google Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary-layer up to R-theta = 1410. J. Fluid Mech. 187, 61–98.Google Scholar
Stull, R. B. 1988 An Introduction to Boundary Layer Meteorology. Kluwer Academic Publishers.Google Scholar
Venayagamoorthy, S. K. & Koseff, J. R. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1.Google Scholar
Wyngaard, J. C. 2010 Turbulence in The Atmosphere. Cambridge University Press.Google Scholar
Yamada, T. 1975 The critical Richardson number and the ratio of the eddy transport coefficients obtained from a turbulence closure model. J. Atmos. Sci. 32 (5), 926–933.Google Scholar
You, J., Yoo, J. Y. & Choi, H. 2003 Direct numerical simulation of heated vertical air flows in fully developed turbulent mixed convection. Intl J. Heat Mass Transfer 46 (9), 1613–1627.Google Scholar
Zilitinkevich, S. 2002 Third-order transport due to internal waves and non-local turbulence in the stably stratified surface layer. Q. J. R. Meteorol. Soc. 128 (581), 913–925.Google Scholar
Zilitinkevich, S. S. 1973 Shear convection. Boundary-Layer Meteorol. 3 (4), 416–423.Google Scholar