Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T14:31:03.241Z Has data issue: false hasContentIssue false
  • English
  • Français

On the propagation of gravity currents over and through a submerged array of circular cylinders

Published online by Cambridge University Press:  13 October 2017

Jian Zhou ,
Claudia Cenedese ,
Tim Williams ,
Megan Ball ,
Subhas K. Venayagamoorthy Open the ORCID record for Subhas K. Venayagamoorthy [Opens in a new window]  and
Roger I. Nokes Open the ORCID record for Roger I. Nokes [Opens in a new window]
Jian Zhou
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523, USA
Claudia Cenedese
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
Tim Williams
Affiliation:
Department of Civil and Natural Resources Engineering, University of Canterbury, Private Bag 4800, Christchurch 8140, New Zealand
Megan Ball
Affiliation:
Department of Civil and Natural Resources Engineering, University of Canterbury, Private Bag 4800, Christchurch 8140, New Zealand
Subhas K. Venayagamoorthy*
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523, USA
Roger I. Nokes
Affiliation:
Department of Civil and Natural Resources Engineering, University of Canterbury, Private Bag 4800, Christchurch 8140, New Zealand
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The propagation of full-depth lock-exchange bottom gravity currents past a submerged array of circular cylinders is investigated using laboratory experiments and large eddy simulations. Firstly, to investigate the front velocity of gravity currents across the whole range of array density 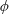$\unicode[STIX]{x1D719}$ (i.e. the volume fraction of solids), the array is densified from a flat bed (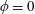$\unicode[STIX]{x1D719}=0$) towards a solid slab (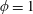$\unicode[STIX]{x1D719}=1$) under a particular submergence ratio 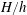$H/h$, where 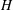$H$ is the flow depth and 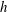$h$ is the array height. The time-averaged front velocity in the slumping phase of the gravity current is found to first decrease and then increase with increasing 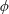$\unicode[STIX]{x1D719}$. Next, a new geometrical framework consisting of a streamwise array density 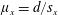$\unicode[STIX]{x1D707}_{x}=d/s_{x}$ and a spanwise array density 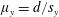$\unicode[STIX]{x1D707}_{y}=d/s_{y}$ is proposed to account for organized but non-equidistant arrays (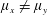$\unicode[STIX]{x1D707}_{x}\neq \unicode[STIX]{x1D707}_{y}$), where 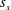$s_{x}$ and 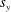$s_{y}$ are the streamwise and spanwise cylinder spacings, respectively, and 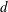$d$ is the cylinder diameter. It is argued that this two-dimensional parameter space can provide a more quantitative and unambiguous description of the current–array interaction compared with the array density given by 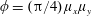$\unicode[STIX]{x1D719}=(\unicode[STIX]{x03C0}/4)\unicode[STIX]{x1D707}_{x}\unicode[STIX]{x1D707}_{y}$. Both in-line and staggered arrays are investigated. Four dynamically different flow regimes are identified: (i) through-flow propagating in the array interior subject to individual cylinder wakes (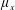$\unicode[STIX]{x1D707}_{x}$: small for in-line array and arbitrary for staggered array; 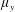$\unicode[STIX]{x1D707}_{y}$: small); (ii) over-flow propagating on the top of the array subject to vertical convective instability (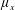$\unicode[STIX]{x1D707}_{x}$: large; 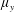$\unicode[STIX]{x1D707}_{y}$: large); (iii) plunging-flow climbing sparse close-to-impermeable rows of cylinders with minor streamwise intrusion (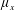$\unicode[STIX]{x1D707}_{x}$: small; 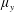$\unicode[STIX]{x1D707}_{y}$: large); and (iv) skimming-flow channelized by an in-line array into several subcurrents with strong wake sheltering (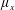$\unicode[STIX]{x1D707}_{x}$: large; 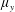$\unicode[STIX]{x1D707}_{y}$: small). The most remarkable difference between in-line and staggered arrays is the non-existence of skimming-flow in the latter due to the flow interruption by the offset rows. Our analysis reveals that as 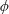$\unicode[STIX]{x1D719}$ increases, the change of flow regime from through-flow towards over- or skimming-flow is responsible for increasing the gravity current front velocity.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 394 - 417
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, S., Julien, P. Y. & Venayagamoorthy, S. K. 2012 Numerical simulation of particle-driven gravity currents. Environ. Fluid Mech 12, 495–513.Google Scholar
Cantero, M. I., Lee, J. R., Balachandar, S. & Garcia, M. H. 2007 On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.Google Scholar
Cenedese, C., Nokes, R. & Hyatt, J. 2016 Lock-exchange gravity currents over rough bottoms. Environ. Fluid Mech.; doi:10.1007/s10652-016-9501-0.Google Scholar
Harvey, J. W., Conklin, M. H. & Koelsch, R. S. 2003 Predicting changes in hydrologic retention in an evolving semi-arid alluvial stream. Adv. Water Resour. 26, 939–950.Google Scholar
Hatcher, L., Hogg, A. J. & Woods, A. W. 2000 The effects of drag on turbulent gravity currents. J. Fluid Mech. 416, 297–314.Google Scholar
Hirt, C. W. 1993 Volume-fraction techniques: power tools for wind engineering. J. Wind Engng Ind. Aerodyn. 46–47, 327–338.Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.Google Scholar
Jamali, M., Zhang, X & Nepf, H. M. 2008 Exchange flow between a canopy and open water. J. Fluid Mech. 611, 237–254.Google Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
van Leer, B. 1977 Towards the ultimate conservative difference scheme. IV. A new approach to numerical convection. J. Comput. Phys. 23, 276–299.Google Scholar
Nepf, H., Ghisalberti, M., White, B. & Murphy, E. 2007 Retention time and dispersion associated with submerged aquatic canopies. Water Resour. Res. 43, W04422.Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Nokes, R. 2016 Streams 2.05 – System Theory and Design. University of Canterbury, Christchurch.Google Scholar
Oertel, M. & Schlenkhoff, A. 2012 Crossbar block ramps: flow regimes, energy dissipation, friction factors, and drag forces. J. Hydraul. Engng 138 (5), 440–448.Google Scholar
Oke, T. R. 1988 Boundary Layer Climates, 2nd edn. Methuen.Google Scholar
Ooi, S. K., Constantinescu, G. & Weber, L. 2009 Numerical simulations of lock-exchange compositional gravity current. J. Fluid Mech. 635, 361–388.CrossRefGoogle Scholar
Ozan, A. Y., Constantinescu, G. & Hogg, A. J. 2015 Lock-exchange gravity currents propagating in a channel containing an array of obstacles. J. Fluid Mech. 765, 544–575.Google Scholar
Ozan, A. Y., Constantinescu, G. & Nepf, H. 2016 Free-surface gravity currents propagating in an open channel containing a porous layer at the free surface. J. Fluid Mech. 809, 601–627.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a retangular channel. J. Fluid Mech. 135, 95–110.CrossRefGoogle Scholar
Savage, B. M. & Johnson, M. C. 2001 Flow over ogee spillways: physical and numerical models cast study. J. Hydraul. Engng 127 (8), 640–649.Google Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.Google Scholar
Simpson, J. E. 1997 Gravity Currents: in the Environment and Laboratory, 2nd edn. Cambridge University Press.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic experiments. Mon. Weath. Rev. 91, 99–164.2.3.CO;2>CrossRefGoogle Scholar
Tanino, Y., Nepf, H. M. & Kulis, P. S. 2005 Gravity currents in aquatic canopies. Water Resour. Res. 41, W12402.CrossRefGoogle Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2011 Lock-exchange gravity currents with a high volume of release propagating over a periodic array of obstacles. J. Fluid Mech. 672, 570–605.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2012 Tail structure and bed friction velocity distribution of gravity currents propagating over an array of obstacles. J. Fluid Mech. 694, 252–291.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2014 Lock-exchange gravity currents with a low volume of release propagating over an array of obstacles. J. Geophys. Res. Oceans 119, 2752–2768.Google Scholar
Ungarish, M. & Huppert, H. E. 2000 High-Reynolds number gravity currents over a porous boundary: shallow-water solutions and box-model approximations. J. Fluid Mech. 418, 1–23.CrossRefGoogle Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. J. Fluid Mech. 28, 477–539.Google Scholar
Yao, G. F.2004 Development of new pressure-velocity solvers in FLOW-3D. Tech. Rep. FSI-04-TN68, Flow Science, Inc.Google Scholar
Zhang, X. & Nepf, H. M. 2008 Density-driven exchange flow between open water and an aquatic canopy. Water Resour. Res. 44, W08417.Google Scholar
Zhang, X. & Nepf, H. M. 2011 Exchange flow between open water and floating vegetation. Environ. Fluid Mech. 11, 531–546.Google Scholar
Zhou, J. & Venayagamoorthy, S. K. 2017 Numerical simulations of intrusive gravity currents interacting with a bottom-mounted obstacle in a continuously stratified ambient. Environ. Fluid Mech. 17, 191–209.Google Scholar