Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T18:19:21.929Z Has data issue: false hasContentIssue false
  • English
  • Français

On the origin of the flip–flop instability of two side-by-side cylinder wakes

Published online by Cambridge University Press:  21 February 2014

M. Carini ,
F. Giannetti  and
F. Auteri
M. Carini
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
F. Giannetti
Affiliation:
Dipartimento di Ingegneria Industriale, Università degli studi di Salerno, via Ponte don Melillo, 84084 Fisciano (SA), Italy
F. Auteri*
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

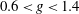In this work the flip–flop instability occurring in the flow past two side-by-side circular cylinders is numerically investigated within the range of non-dimensional gap spacing $0.6<g<1.4$ and Reynolds number 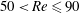$50<Re\leq 90$. The inherent two-dimensional flow pattern is characterized by an asymmetric unsteady wake (with respect to the horizontal axis of symmetry) with the gap flow being deflected alternatively toward one of the cylinders. Such behaviour has been ascribed by other authors to a bistability of the flow, and therefore termed flip–flop. In contrast, the simulations performed herein provide new evidence that at low Reynolds numbers the flip–flopping state develops through an instability of the in-phase synchronized vortex shedding between the two cylinder wakes. This new scenario is confirmed and explained by means of a linear global stability investigation of the in-phase periodic base flow. The Floquet analysis reveals indeed that a pair of complex-conjugate multipliers becomes unstable having the same low frequency as the gap flow flip-over. The neutral curve of this secondary instability is tracked within the above range of gap spacing. The spatiotemporal shape of the unstable Floquet mode is then analysed and its structural sensitivity is considered in order to identify the ‘core’ region of the flip–flop instability mechanism.

JFM classification

Instability: Instability Wakes/Jets: Wakes/Jets Wakes/Jets: Vortex streets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 552 - 576
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hoepffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.CrossRefGoogle Scholar
Afgan, I., Kahil, Y., Benhamadouche, S. & Sagaut, P. 2011 Large eddy simulation of the flow around single and two side-by-side cylinders at subcritical Reynolds numbers. Phys. Fluids 23, 075101.Google Scholar
Akinaga, T. & Mizushima, J. 2005 Linear stability of flows past two circular cylinders in a side-by-side arrangement. J. Phys. Soc. Japan 74 (5), 1366–1369.Google Scholar
Bearman, P. W. & Wadcock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61, 499–511.Google Scholar
Bittanti, S. & Colaneri, P. 2009 Periodic Systems: Filtering and Control (Communication and Control Engineering). Springer.Google Scholar
Camarri, S. & Giannetti, F. 2010 Effect of confinement on three-dimensional stability in the wake of a circular cylinder. J. Fluid Mech. 642, 477–487.Google Scholar
Camarri, S. & Iollo, A. 2010 Feedback control of the vortex-shedding instability based on sensitivity analysis. Phys. Fluids 22, 094102.Google Scholar
Chen, L., Tu, J. Y. & Yeoh, G. H. 2003 Numerical simulation of turbulent wake flows behind two side-by-side cylinders. J. Fluids Struct. 18, 387–403.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 156, 209–240.Google Scholar
Coddington, E. & Levinson, N. 1955 Theory of Ordinary Differential Equations. McGraw-Hill.Google Scholar
Davis, T. A. 2004 Algorithm 832: UMFPACK, an unsymmetric-pattern multifrontal method. ACM Trans. Math. Software 30 (2), 196–199.CrossRefGoogle Scholar
Drazin, P. G. 2002 Introduction to Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.Google Scholar
Giannetti, F., Fabre, D., Tchoufag, J. & Luchini, P. 2012 The steady oblique path of buoyancy-driven rotating spheres. In 9th European Fluid Mechanics Conference, Rome, 9–13 September 2012 .Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid. Mech. 581, 167–197.CrossRefGoogle Scholar
Giannetti, F., Luchini, P. & Marino, L. 2009 Characterization of the three-dimensional instability in a lid-driven cavity by an adjoint-based analysis. In Seventh IUTAM Symposium on Laminar–Turbulent Transition (ed. Schlatter, P. & Henningson, D. S.), pp. 96–97. KTH.Google Scholar
Haque, S., Lashgari, I., Brandt, L. & Giannetti, F. 2012 Stability of fluids with shear-dependent viscosity in the lid-driven cavity. J. Non-Newtonian Fluid Mech. 173, 49–61.Google Scholar
Ilak, M., Schlatter, P., Bagheri, S. & Henningson, D. 2011 Bifurcation and stability analysis of a jet in crossflow. Part 1: Onset of global instability at a low velocity ratio. J. Fluid Mech. 696, 94–121.Google Scholar
Kang, S. 2003 Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers. Phys. Fluids 15, 2486–2498.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 196, 431–448.Google Scholar
Lashgari, I., Pralits, J. O., Giannetti, F. & Brandt, L. 2012 First instability of the flow of shear-thinning and shear-thickening fluids past a circular cylinder. J. Fluid Mech. 701, 201–227.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users Guide. SIAM.Google Scholar
Luchini, P. 2011 Private communication.Google Scholar
Luchini, P., Giannetti, F. & Pralits, J. O. 2008 Structural sensitivity of linear and nonlinear global modes. In Proceedings of the 5th AIAA Theoretical Fluid Mechanics Conference, 23–26 June, Seattle, Washington pp. 1–19. Curran Associates Inc.Google Scholar
Luchini, P., Pralits, J. O. & Giannetti, F. 2007 Structural sensitivity of the finite-amplitude vortex shedding behind a circular cylinder. In Proceedings of the 2nd IUTAM Symposium on unsteady separated flows and their control, 18–22 June 2007, Corfu, Greece (ed. Braza, M. & Houringan, K.), pp. 151–160. Springer.Google Scholar
Lust, K., Roose, D., Spence, A. & Champneys, A. R. 1998 An adaptive Newton–Picard algorithm with subspace iteration for computing periodic solutions. SIAM J. Sci. Comp. 19 (4), 1118–1209.Google Scholar
Marino, L. & Luchini, P. 2009 Adjoint analysis of the flow over a forward-facing step. Theor. Comp. Fluid Dyn. 23, 37–54.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluid Mech. 660, 499–526.Google Scholar
Mizushima, J. & Ino, Y. 2008 Stability of flows past a pair of circular cylinders in a side-by-side arrangement. J. Fluid Mech. 595, 491–507.Google Scholar
Peschard, I. & Le Gal, P. 1996 Coupled wakes of cylinders. Phys. Rev. Lett. 77, 3122–3125.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 1–24.CrossRefGoogle Scholar
Rai, M. M. & Moin, P. 1991 Direct simulations of turbulent flow using finite-difference schemes. J. Comp. Phys. 96, 15–53.Google Scholar
Robichaux, J., Balanchadar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of a square cylinder. Phys. Fluids 11, 560–578.Google Scholar
Shroff, G. M. & Keller, H. B. 1993 Stabilization of unstable procedures: the recursive projection method. SIAM J. Numer. Anal. 30 (4), 1099–1120.Google Scholar
Sumner, D. 2010 Two circular cylinders in cross-flows: a review. J. Fluids Struct. 26, 849–899.Google Scholar
Sumner, D., Wong, S. S. T., Price, S. J. & Païdoussis, M. P. 1999 Fluid behavior of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 13, 309–338.Google Scholar
Trottenberg, U., Oosterlee, C. & Schüller, A. 2001 Multigrid. Academic Press.Google Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2011 Transition to turbulence through steep global-modes cascade in an open rotating cavity. J. Fluid Mech. 688, 493–506.Google Scholar
Wang, Z. J., Zhou, Y. & Li, H. 2002 Flow-visualization of a two side-by-side cylinder wake. J. Flow Visual. Image Process. 9, 123–138.Google Scholar
Williamson, C. H. K. 1985 Evolution of a single wake behind a pair of bluff bodies. J. Fluid Mech. 159, 1–18.Google Scholar
Zdravkovich, M. M. 1977 Review of flow interference between two circular cylinders in various arrangement. Trans. ASME I: J. Fluids Engng 99, 618–633.Google Scholar
Zhou, Y., Zhang, H. J. & Yiu, M. W. 2002 The turbulent wake of two side-by-side circular cylinders. J. Fluid Mech. 458, 303–332.Google Scholar