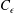 $C_{\unicode[STIX]{x1D716}}$ in decaying turbulence
$C_{\unicode[STIX]{x1D716}}$ in decaying turbulencePublished online by Cambridge University Press: 15 March 2017
The Reynolds number dependence of the non-dimensional mean turbulent kinetic energy dissipation rate
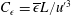 $C_{\unicode[STIX]{x1D716}}=\overline{\unicode[STIX]{x1D716}}L/u^{\prime 3}$
(where
$C_{\unicode[STIX]{x1D716}}=\overline{\unicode[STIX]{x1D716}}L/u^{\prime 3}$
(where
 $\unicode[STIX]{x1D716}$
is the mean turbulent kinetic energy dissipation rate,
$\unicode[STIX]{x1D716}$
is the mean turbulent kinetic energy dissipation rate,
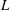 $L$
is an integral length scale and
$L$
is an integral length scale and
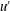 $u^{\prime }$
is the velocity root-mean-square) is investigated in decaying turbulence. Expressions for
$u^{\prime }$
is the velocity root-mean-square) is investigated in decaying turbulence. Expressions for
 $C_{\unicode[STIX]{x1D716}}$
in homogeneous isotropic turbulent (HIT), as approximated by grid turbulence, and in local HIT, as on the axis of the far field of a turbulent round jet, are developed from the Navier–Stokes equations within the framework of a scale-by-scale energy budget. The analysis shows that when turbulence decays/evolves in compliance with self-preservation (SP),
$C_{\unicode[STIX]{x1D716}}$
in homogeneous isotropic turbulent (HIT), as approximated by grid turbulence, and in local HIT, as on the axis of the far field of a turbulent round jet, are developed from the Navier–Stokes equations within the framework of a scale-by-scale energy budget. The analysis shows that when turbulence decays/evolves in compliance with self-preservation (SP),
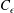 $C_{\unicode[STIX]{x1D716}}$
remains constant for a given flow condition, e.g. a given initial Reynolds number. Measurements in grid turbulence, which does not satisfy SP, and on the axis in the far field of a round jet, which does comply with SP, show that
$C_{\unicode[STIX]{x1D716}}$
remains constant for a given flow condition, e.g. a given initial Reynolds number. Measurements in grid turbulence, which does not satisfy SP, and on the axis in the far field of a round jet, which does comply with SP, show that
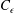 $C_{\unicode[STIX]{x1D716}}$
decreases in the former case and remains constant in the latter, thus supporting the theoretical results. Further, while
$C_{\unicode[STIX]{x1D716}}$
decreases in the former case and remains constant in the latter, thus supporting the theoretical results. Further, while
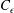 $C_{\unicode[STIX]{x1D716}}$
can remain constant during the decay for a given initial Reynolds number, both the theory and measurements show that it decreases towards a constant,
$C_{\unicode[STIX]{x1D716}}$
can remain constant during the decay for a given initial Reynolds number, both the theory and measurements show that it decreases towards a constant,
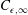 $C_{\unicode[STIX]{x1D716},\infty }$
, as
$C_{\unicode[STIX]{x1D716},\infty }$
, as
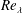 $Re_{\unicode[STIX]{x1D706}}$
increases. This trend, in agreement with existing data, is not inconsistent with the possibility that
$Re_{\unicode[STIX]{x1D706}}$
increases. This trend, in agreement with existing data, is not inconsistent with the possibility that
 $C_{\unicode[STIX]{x1D716}}$
tends to a universal constant.
$C_{\unicode[STIX]{x1D716}}$
tends to a universal constant.