Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T08:37:26.751Z Has data issue: false hasContentIssue false
  • English
  • Français

On the nonlinear destabilization of stably stratified shear flow

Published online by Cambridge University Press:  15 August 2013

Nadia Mkhinini ,
Thomas Dubos  and
Philippe Drobinski
Nadia Mkhinini
Affiliation:
Laboratoire de Météorologie Dynamique/IPSL, École Polytechnique, 91128 Palaiseau, France
Thomas Dubos*
Affiliation:
Laboratoire de Météorologie Dynamique/IPSL, École Polytechnique, 91128 Palaiseau, France
Philippe Drobinski
Affiliation:
Laboratoire de Météorologie Dynamique/IPSL, École Polytechnique, 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A weakly nonlinear analysis of the bifurcation of the stratified Ekman boundary-layer flow near a critical bulk Richardson number is conducted and compared to a similar analysis of a continuously stratified parallel shear flow subject to Kelvin–Helmholtz instability. Previous work based on asymptotic expansions and predicting supercritical bifurcation at Prandtl number 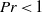$Pr\lt 1$ and subcritical bifurcation at $Pr\gt 1$ for the parallel base flow is confirmed numerically and through fully nonlinear temporal simulations. When applied to the non-parallel Ekman flow, weakly nonlinear analysis and fully nonlinear calculations confirm that the nature of the bifurcation is dominantly controlled by 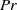$Pr$, although a sharp threshold at 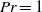$Pr= 1$ is not found. In both flows the underlying physical mechanism is that the mean flow adjusts so as to induce a viscous (respectively diffusive) flux of momentum (respectively buoyancy) that balances the vertical flux induced by the developing instability, leading to a weakening of the mean shear and mean stratification. The competition between the former nonlinear feedback, which tends to be stabilizing, and the latter, which is destabilizing and strongly amplified as 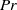$Pr$ increases, determines the supercritical or subcritical character of the bifurcation. That essentially the same competition is at play in both the parallel shear flow and the Ekman flow suggests that the underlying mechanism is valid for complex, non-parallel stratified shear flows.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 731 , 25 September 2013 , pp. 443 - 460
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, R. A. 1972 On the inflection point instability of a stratified Ekman boundary layer. J. Atmos. Sci 29 (5), 850–859.Google Scholar
Brown, S. N., Rosen, A. S. & Maslowe, S. A. 1981 The evolution of a quasi-steady critical layer in a stratified viscous shear layer. Proc. R. Soc. Lond. A 375 (1761), 271–293.Google Scholar
Churilov, S. M. & Shukhman, I. G. 1987 Nonlinear stability of a stratified shear flow: a viscous critical layer. J. Fluid Mech. 180, 1–20.CrossRefGoogle Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1990 A numerical study of the turbulent Ekman layer. J. Fluid Mech. 213, 313–348.Google Scholar
Coleman, G. N., Ferziger, J. H. & Spalart, P. R. 1992 Direct simulation of the stably stratified turbulent Ekman layer. J. Fluid Mech. 244, 677–712.Google Scholar
Cortesi, A. B., Yadigaroglu, G. & Banerjee, S. 1998 Numerical investigation of the formation of three-dimensional structures in stably-stratified mixing layers. Phys. Fluids 10 (6), 1449–1473.Google Scholar
Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating-disc boundary layer. J. Fluid Mech. 486, 287–329.CrossRefGoogle Scholar
Dubos, T., Barthlott, C. & Drobinski, P. 2008 Emergence and secondary instability of Ekman layer rolls. J. Atmos. Sci 65 (7), 2326–2342.Google Scholar
Ekman, V. W. 1905 On the influence of the earth’s rotation on ocean currents. Ark. Mat. Astron. Fys. 2 (11), 1–54.Google Scholar
Foster, R. C. 1996 An analytic model for planetary boundary layer roll vortices. PhD thesis, University of Washington.Google Scholar
Fujimura, K. 1989 The equivalence between two perturbation methods in weakly nonlinear stability theory for parallel shear flows. Proc. R. Soc. Lond. A 424 (1867), 373–392.Google Scholar
Haeusser, T. M. & Leibovich, S. 2003 Pattern formation in the marginally unstable Ekman layer. J. Fluid Mech. 479, 125–144.CrossRefGoogle Scholar
Herbert, T. 1983 On perturbation methods in nonlinear stability theory. J. Fluid Mech. 126, 167–186.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10 (4), 509–512.Google Scholar
Iooss, G., Nielsen, H. & True, H. 1978 Bifurcation of the stationary Ekman flow into a stable periodic flow. Arch. Rat. Mech. 68 (3), 227–256.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985 The effect of Prandtl number on the evolution and stability of Kelvin–Helmholtz billows. Geophys. Astrophys. Fluid Dyn. 32 (1), 23–60.Google Scholar
Lilly, D. K. 1966 On the instability of Ekman boundary flow. J. Atmos. Sci. 23 (481–494).Google Scholar
Lingwood, R. J. 1997 Absolute instability of the Ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.Google Scholar
Lott, F. & Teitelbaum, H. 1992 Nonlinear dissipative critical level interaction in a stratified shear flow: instabilities and gravity waves. Geophys. Astrophys. Fluid Dyn. 66 (1–4), 133–167.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.Google Scholar
Mkhinini, N., Dubos, T. & Drobinski, P. 2013 Secondary instability of stratified Ekman layer. J. Fluid Mech. 728, 29–57.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Pier, B. 2003 Finite-amplitude crossflow vortices, secondary instability and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27 (3), 465–492.Google Scholar
Spalart, P. R. 1989 Theoretical and numerical study of a three-dimensional turbulent boundary layer. J. Fluid Mech. 205, 319–340.Google Scholar
Staquet, C. 2009 Mixing in a stably stratified shear layer: two- and three-dimensional numerical experiments. Fluid. Dyn. Res., 27, 367.Google Scholar
Stuart, J. T. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9 (3), 353–370.Google Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2008 The elephant mode between two rotating disks. J. Fluid Mech. 598, 451–464.Google Scholar
Watson, J. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. Part 2. The development of a solution for plane Poiseuille flow and for plane Couette flow. J. Fluid Mech. 9 (3), 371–389.Google Scholar