Article contents
On the nonlinear behaviour of the Rayleigh–Taylor instability with a tangential electric field for inviscid and perfect dielectric fluids
Published online by Cambridge University Press: 09 March 2023
Abstract
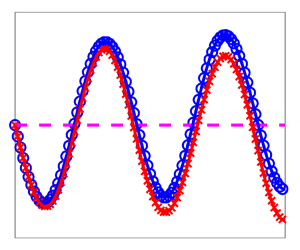
Fluid interfacial instability induced by gravity or external acceleration, known as the Rayleigh–Taylor instability, plays an important role in both scientific research and industrial application. How to control this instability is challenging. Researchers have been actively exploring the suppression method of applying electric fields parallel to dielectric fluid interfaces. The instability is characterized by the penetration of fingers at the interface. The velocities at the finger tips are the most important quantities since they characterize how fast the penetration occurs. The dynamics of the fingers is nonlinear. We present a nonlinear perturbation procedure for determining the amplitude and velocity of fingers at a Rayleigh–Taylor unstable interface between two incompressible, inviscid, immiscible and perfectly dielectric fluids in the presence of a horizontal electric field in two dimensions. The analytic formulas are displayed explicitly up to the third order of the initial disturbance. The comparison with the data from numerical simulations based on the vortex sheet method shows the theoretical formulas can capture well the nonlinear behaviour of the fingers. It is known that the interplay between the electric field and the fluids can lead to the suppression of interfacial instability. We further analyse the electrical force along the interface and show how this force leads to the instability suppression in our setting. It has been reported numerically in the literature that switching the electric permittivities of the fluids leads to quantitative differences in finger velocity. We show theoretically this phenomenon can only be explained by the nonlinear behaviour of the system.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 5
- Cited by



