Published online by Cambridge University Press: 17 January 2023
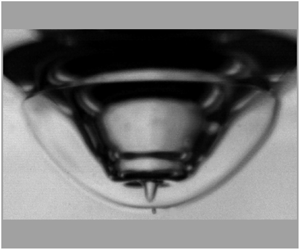
We study drop impacts on an immiscible viscous liquid pool and investigate the formation of droplet surface craters using experimental and theoretical analyses. We attribute the formation of air craters to the rapid deceleration of the droplet due to viscous drag force. The droplet response to the external impulsive decelerating force induces oscillatory modes on the surface exposed to the air forming capillary waves that superimpose to form air craters of various shapes and sizes. We introduce a non-dimensional parameter ( ${\varGamma }$), that is, the ratio of the drag force to the capillary force acting on the droplet. We show that
${\varGamma }$), that is, the ratio of the drag force to the capillary force acting on the droplet. We show that  ${\varGamma }$ is directly proportional to the capillary number. We show that droplets forming air craters of significant depths have
${\varGamma }$ is directly proportional to the capillary number. We show that droplets forming air craters of significant depths have  ${\varGamma }>1$. Further, we demonstrate that Legendre polynomials can locally approximate the central air crater jet profile. We also decipher that the air crater response time scale (
${\varGamma }>1$. Further, we demonstrate that Legendre polynomials can locally approximate the central air crater jet profile. We also decipher that the air crater response time scale ( $T$) varies as the square root of impact Weber number (
$T$) varies as the square root of impact Weber number ( $T\sim We^{1/2}$). Further, we generalize the local droplet response with a global response model for low impact energies based on an eigenvalue problem. We represent the penetrating drop as a constrained Rayleigh drop problem with a dynamic contact line. The air–water interface dynamics is analysed using an inviscid droplet deformation model for small deformation amplitudes. The local and global droplet response theories conform with each other and depict that the deformation profiles could be represented as a linear superposition of eigenmodes in Legendre polynomial basis. We unearth that the droplet response in an immiscible impact system differs from the miscible impact systems due to the presence of such a dynamic contact line.
$T\sim We^{1/2}$). Further, we generalize the local droplet response with a global response model for low impact energies based on an eigenvalue problem. We represent the penetrating drop as a constrained Rayleigh drop problem with a dynamic contact line. The air–water interface dynamics is analysed using an inviscid droplet deformation model for small deformation amplitudes. The local and global droplet response theories conform with each other and depict that the deformation profiles could be represented as a linear superposition of eigenmodes in Legendre polynomial basis. We unearth that the droplet response in an immiscible impact system differs from the miscible impact systems due to the presence of such a dynamic contact line.