Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T21:14:48.004Z Has data issue: false hasContentIssue false
  • English
  • Français

On the longitudinal optimal perturbations to inviscid plane shear flow: formal solution and asymptotic approximation

Published online by Cambridge University Press:  26 November 2013

C. Arratia  and
J.-M. Chomaz
C. Arratia*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), École Polytechnique–CNRS, F-91128 Palaiseau, France LFMI, École Polytechnique Fédérale de Lausanne, CH1015 Lausanne, Switzerland
J.-M. Chomaz
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), École Polytechnique–CNRS, F-91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the longitudinal linear optimal perturbations (which maximize the energy gain up to a prescribed time 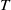$T$) to inviscid parallel shear flow, which present unbounded energy growth due to the lift-up mechanism. Using the phase invariance with respect to time, we show that for an arbitrary base flow profile and optimization time, the computation of the optimal longitudinal perturbation reduces to the resolution of a single one-dimensional eigenvalue problem valid for all times. The optimal perturbation and its amplification are then derived from the lowest eigenvalue and its associated eigenfunction, while the remainder of the infinite set of eigenfunctions provides an orthogonal base for decomposing the evolution of arbitrary perturbations. With this new formulation we obtain, asymptotically for large spanwise wavenumber 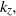${k}_{z} , $ a prediction of the optimal gain and the localization of inviscid optimal perturbations for the two main classes of parallel flows: free shear flow with an inflectional velocity profile, and wall-bounded flow with maximum shear at the wall. We show that the inviscid optimal perturbations are localized around the point of maximum shear in a region with a width scaling like 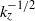${ k}_{z}^{- 1/ 2} $ for free shear flow, and like 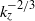${ k}_{z}^{- 2/ 3} $ for wall-bounded shear flows. This new derivation uses the stationarity of the base flow to transform the optimization of initial conditions in phase space into the optimization of a temporal phase along each trajectory, and an optimization among all trajectories labelled by their intersection with a codimension-1 subspace. The optimization of the time phase directly imposes that the initial and final energy growth rates of the optimal perturbation should be equal. This result requires only time invariance of the base flow, and is therefore valid for any linear optimal perturbation problem with stationary base flow.

JFM classification

Boundary Layers: Boundary Layers Instability: Instability Wakes/Jets: Shear layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 737 , 25 December 2013 , pp. 387 - 411
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. 1964 Handbook of Mathematical Functions. Dover.Google Scholar
Arratia, C., Caulfield, C. P. & Chomaz, J.-M. 2013 Transient perturbation growth in time-dependent mixing layers. J. Fluid Mech. 717, 90–133.CrossRefGoogle Scholar
Ballentine, L. E. 1998 Quantum Mechanics. Prentice Hall.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids A 5 (6), 1390–1400.CrossRefGoogle Scholar
Gustavsson, L. H. 1991 Energy growth of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.Google Scholar
Hanifi, A. & Henningson, D. S. 1998 The compressible inviscid algebraic instability for streamwise independent disturbances. Phys. Fluids 10 (8), 1784–1786.Google Scholar
Jerome, J. J. S., Chomaz, J.-M. & Huerre, P. 2012 Transient growth in Rayleigh–Bénard–Poiseuille/Couette convection. Phys. Fluids 24 (4)044103.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98 (2), 243–251.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1977 Quantum Mechanics: Non-Relativistic Theory. Pergamon.Google Scholar
Malik, M., Alam, M. & Dey, J. 2006 Nonmodal energy growth and optimal perturbations in compressible plane Couette flow. Phys. Fluids 18 (3)034103.Google Scholar
Moffatt, H. K. 1967 The interaction of turbulence with strong wind shear. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarski, V. I.), pp. 139–154.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Teschl, G. 2012 Ordinary Differential Equations and Dynamical Systems. Graduate Studies in Mathematics Series, vol. 140, American Mathematical Society.Google Scholar