Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T17:46:09.325Z Has data issue: false hasContentIssue false
  • English
  • Français

On the linear receptivity of trailing vortices

Published online by Cambridge University Press:  03 December 2020

Tobias Bölle Open the ORCID record for Tobias Bölle [Opens in a new window] ,
Vincent Brion Open the ORCID record for Vincent Brion [Opens in a new window] ,
Jean-Christophe Robinet Open the ORCID record for Jean-Christophe Robinet [Opens in a new window] ,
Denis Sipp Open the ORCID record for Denis Sipp [Opens in a new window]  and
Laurent Jacquin
Tobias Bölle*
Affiliation:
DAAA, ONERA-The French Aerospace Lab, Université Paris Saclay, 92190Meudon, France
Vincent Brion
Affiliation:
DAAA, ONERA-The French Aerospace Lab, Université Paris Saclay, 92190Meudon, France
Jean-Christophe Robinet
Affiliation:
DynFLuid, Arts et Métiers Institute of Technology, CNAM, HESAM University, 75013Paris, France
Denis Sipp
Affiliation:
DAAA, ONERA-The French Aerospace Lab, Université Paris Saclay, 92190Meudon, France
Laurent Jacquin
Affiliation:
DAAA, ONERA-The French Aerospace Lab, Université Paris Saclay, 92190Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

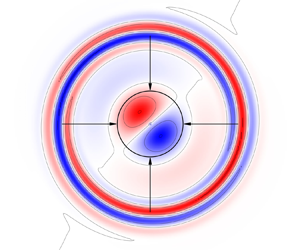
The present work investigates the excitation process by which free-stream disturbances are transformed into vortex-core perturbations. This problem of receptivity is modelled in terms of the resolvent in frequency space as the linear response to forcing. This formulation of receptivity suggests that non-normality of the resolvent is necessary to allow free-stream disturbances to excite the vortex core. Considering a local (in frequency) measure of non-normality, we show that vortices are frequency-selectively non-normal in a narrow frequency band of retrograde perturbations while the rest of the range is governed by an effectively normal operator, thus not contributing to receptivity. Canonical decomposition of the resolvent reveals that vortices are most susceptible to coiled filaments localised about the critical layer that induce bending waves on the core. Considering Lamb–Oseen, Batchelor and Moore–Saffman vortices as reference-flow models, we find free-stream receptivity to be essentially generic and independent of the axial wavelength on the considered range. A stochastic interpretation of the results could be a model for trailing-vortex meandering.

JFM classification

Vortex Flows: Vortex dynamics Mathematical Foundations: General fluid mechanics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A8
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abid, M. 2008 Nonlinear mode selection in a model of trailing line vortices. J. Fluid Mech. 605, 19–45.CrossRefGoogle Scholar
Antkowiak, A. 2005 Dynamique aux temps courts d'un tourbillon isolé. PhD thesis, Université Paul Sabatier de Toulouse.Google Scholar
Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16 (1), L1–L4.CrossRefGoogle Scholar
Arnol'd, V. I. 1992 Ordinary Differential Equations. Springer.Google Scholar
Ash, R. L. & Khorrami, M. R. 1995 Vortex stability. In Fluid Vortices (ed. Green, S. I.), pp. 317–372. Springer.Google Scholar
Bailey, S. C. C., Pentelow, S., Ghimire, H. C., Estejab, B., Green, M. A. & Tavoularis, S. 2018 Experimental investigation of the scaling of vortex wandering in turbulent surroundings. J. Fluid Mech. 843, 722–747.CrossRefGoogle Scholar
Baker, G. R., Barker, S. J., Bofah, K. K. & Saffman, P. G. 1974 Laser anemometer measurements of trailing vortices in water. J. Fluid Mech. 65, 325–336.CrossRefGoogle Scholar
Bandyopadhyay, P. R., Stead, D. J. & Ash, R. L. 1991 Organized nature of a turbulent trailing vortex. AIAA J. 29 (10), 1627–1633.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.CrossRefGoogle Scholar
Blanco-Rodríguez, F. J., Rodríguez-García, J. O., Parras, L. & del Pino, C. 2017 Optimal response of Batchelor vortex. Phys. Fluids 29 (6), 064108.CrossRefGoogle Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wing-tip vortex. J. Fluid Mech. 312, 67–106.CrossRefGoogle Scholar
Engel, K.-J. & Nagel, R. 2000 One-Parameter Semigroups for Linear Evolution Equations. Springer.Google Scholar
Fabre, D. & Jacquin, L. 2004 Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid Mech. 500, 239–262.Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I: autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.2.0.CO;2>CrossRefGoogle Scholar
Feys, J. & Maslowe, S. A. 2014 Linear stability of the Moore-Saffman model for a trailing wingtip vortex. Phys. Fluids 26 (2), 024108.CrossRefGoogle Scholar
Fontane, J., Brancher, P. & Fabre, D. 2008 Stochastic forcing of the Lamb–Oseen vortex. J. Fluid Mech. 613, 233–254.CrossRefGoogle Scholar
Friedman, B. 1962 Principles and Techniques of Applied Mathematics. Courier Dover Publications.Google Scholar
García-Ortiz, J. H., Dominguez-Vazquez, A., Serrano-Aguilera, J. J., Parras, L. & del Pino, C. 2019 A complementary numerical and experimental study of the influence of Reynolds number on theoretical models for wingtip vortices. Comput. Fluids 180, 176–189.CrossRefGoogle Scholar
Guo, Z.-W., Chen, C. & Sun, D.-J. 2011 Stochastic forcing of the Batchelor vortex. In AIP Conference Proceedings, vol. 1376, pp. 302–304. AIP.Google Scholar
Guo, Z.-W. & Sun, D.-J. 2011 Optimal response in the Lamb–Oseen vortex. Phys. Lett. A 375 (36), 3191–3195.CrossRefGoogle Scholar
Gustafson, K. E. & Rao, D. K. M. 1997 Numerical Range. The Field of Values of Linear Operators and Matrices. Springer.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.CrossRefGoogle Scholar
Haller, G., Hadjighasem, A., Farazmand, M. & Huhn, F. 2016 Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 795, 136–173.Google Scholar
Heaton, C. J., Nichols, J. W. & Schmid, P. J. 2009 Global linear stability of the non-parallel Batchelor vortex. J. Fluid Mech. 629, 139–160.CrossRefGoogle Scholar
Heaton, C. J. & Peake, N. 2007 Transient growth in vortices with axial flow. J. Fluid Mech. 587, 271–301.CrossRefGoogle Scholar
Hecht, F. 2018 Freefem++. Version 3.56–2, 3rd edn. Laboratoire Jacques–Louis Lions, Université Pierre et Marie Curie.Google Scholar
Hill, D. C. 1995 Adjoint systems and their role in the receptivity problem for boundary layers. J. Fluid Mech. 292, 183–204.CrossRefGoogle Scholar
Iungo, G. V. 2017 Wandering of a wing-tip vortex: rapid scanning and correction of fixed-point measurements. J. Aircraft 54 (5), 1779–1790.CrossRefGoogle Scholar
Jacobs, R. G. & Durbin, P. A. 1998 Shear sheltering and the continuous spectrum of the Orr–Sommerfeld equation. Phys. Fluids 10 (8), 2006–2011.CrossRefGoogle Scholar
Jacquin, L., Fabre, D., Geffroy, P. & Coustols, E. 2001 The properties of a transport aircraft wake in the extended near field: an experimental study. In 39th AIAA Aerospace Sciences Meeting and Exhibit, AIAA Paper, 2001-1038.Google Scholar
Joseph, D. D. 1976 Stability of Fluid Motions I. Springer.Google Scholar
Karami, M., Hangan, H., Carassale, L. & Peerhossaini, H. 2019 Coherent structures in tornado-like vortices. Phys. Fluids 31 (8), 085118.CrossRefGoogle Scholar
Kato, T. 1980 Perturbation Theory for Linear Operators. Springer.Google Scholar
Kato, T. & Fujita, H. 1962 On the nonstationary Navier–Stokes system. Rend. Seminario Mat. Univ. Padova 32, 243–260.Google Scholar
Landahl, M. T. 1967 A wave-guide model for turbulent shear flow. J. Fluid Mech. 29, 441–459.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon Press.Google Scholar
Le Dizès, S. 2004 Viscous critical-layer analysis of vortex normal modes. Stud. Appl. Maths 112 (4), 315–332.CrossRefGoogle Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1997 Arpack Users Guide: Solution of Large Scale Eigenvalue Problems by Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.CrossRefGoogle Scholar
Mao, X. & Sherwin, S. 2011 Continuous spectra of the Batchelor vortex. J. Fluid Mech. 681, 1–23.CrossRefGoogle Scholar
Mao, X. & Sherwin, S. 2012 Transient growth associated with continuous spectra of the Batchelor vortex. J. Fluid Mech. 697, 35–59.CrossRefGoogle Scholar
Marshall, J. S. & Beninati, M. L. 2005 External turbulence interaction with a columnar vortex. J. Fluid Mech. 540, 221–245.CrossRefGoogle Scholar
McKeon, B. J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, 1–86.CrossRefGoogle Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Melander, M. V. & Hussain, F. 1993 Coupling between a coherent structure and fine-scale turbulence. Phys. Rev. E 48 (4), 2669–2689.CrossRefGoogle ScholarPubMed
Moore, D. W. & Saffman, P. G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333 (1595), 491–508.Google Scholar
Morkovin, M. V. 1988 Recent Insights into Instability and Transition to Turbulence in Open-Flow Systems. Institute for Computer Applications in Science and Engineering, NASA Langley Research Center.Google Scholar
Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.CrossRefGoogle Scholar
Reddy, S. C., Schmid, P. J. & Henningson, D. S. 1993 Pseudospectra of the Orr–Sommerfeld operator. SIAM J. Appl. Maths 53 (1), 15–47.CrossRefGoogle Scholar
Reddy, S. C. & Trefethen, L. N. 1994 Pseudospectra of the convection-diffusion operator. SIAM J. Appl. Maths 54 (6), 1634–1649.CrossRefGoogle Scholar
Riesz, F. & Sz.-Nagy, B. 1956 Functional Analysis. Blackie.Google Scholar
Roy, A. & Subramanian, G. 2014 Linearized oscillations of a vortex column: the singular eigenfunctions. J. Fluid Mech. 741, 404–460.CrossRefGoogle Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34 (1), 291–319.Google Scholar
Sharma, A. S., Mezić, I. & McKeon, B. J. 2016 Correspondence between Koopman mode decomposition, resolvent mode decomposition, and invariant solutions of the Navier–Stokes equations. Phys. Rev. Fluids 1, 032402.CrossRefGoogle Scholar
Sipp, D. & Marquet, O. 2013 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27 (5), 617–635.CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 1–26.CrossRefGoogle Scholar
Sohr, H. 2001 The Navier–Stokes equations: An Elementary Functional Analytic Approach. Springer.Google Scholar
Takahashi, N., Ishii, H. & Miyazaki, T. 2005 The influence of turbulence on a columnar vortex. Phys. Fluids 17 (3), 035105.CrossRefGoogle Scholar
Ting, L., Klein, R. & Knio, O. M. 2007 Vortex Dominated Flows: Analysis and Computation for Multiple Scale Phenomena. Springer Science & Business Media.Google Scholar
Towne, A., Schmidt, O. T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.Google Scholar
Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators. Princeton University Press.CrossRefGoogle Scholar
Van Jaarsveld, J. P. J., Holten, A. P. C., Elsenaar, A., Trieling, R. R. & Van Heijst, G. J. F. 2011 An experimental study of the effect of external turbulence on the decay of a single vortex and a vortex pair. J. Fluid Mech. 670, 214–239.Google Scholar
Viola, F., Arratia, C. & Gallaire, F. 2016 Mode selection in trailing vortices: harmonic response of the non-parallel Batchelor vortex. J. Fluid Mech. 790, 523–552.CrossRefGoogle Scholar
Wang, Z. & Gursul, I. 2012 Unsteady characteristics of inlet vortices. Exp. Fluids 53 (4), 1015–1032.CrossRefGoogle Scholar