Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wu, Jian
Traore, Philippe
and
Tian, Fang-Bao
2013.
Three-dimensional numerical simulation of electro-convection due to strong unipolar charge injection in a cubic cavity.
p.
1038.
Wu, Jian
Traoré, Philippe
Vázquez, Pedro A.
and
Pérez, Alberto T.
2013.
Onset of convection in a finite two-dimensional container due to unipolar injection of ions.
Physical Review E,
Vol. 88,
Issue. 5,
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Fang-Bao Tian
and
Perez, Alberto
2013.
Numerical investigation of electrohydrodynamic plumes for locally enhanced cooling in dielectric liquids.
p.
1.
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Fang-Bao Tian
and
Perez, Alberto
2013.
Effect of the mobility parameter on the oscillatory electro-convection of dielectric liquids subject to strong unipolar charge injection.
p.
1.
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Tian, Fang-Bao
and
Perez, Alberto T.
2014.
Effect of the Mobility Parameter on the Oscillatory Electroconvection of Dielectric Liquids Subject to Strong Unipolar Charge Injection.
IEEE Transactions on Industry Applications,
Vol. 50,
Issue. 4,
p.
2306.
Yazdani, Miad
and
Seyed-Yagoobi, Jamal
2014.
Effect of charge mobility on dielectric liquid flow driven by EHD conduction phenomenon.
Journal of Electrostatics,
Vol. 72,
Issue. 4,
p.
285.
Wu, Jian
Traore, Philippe
Vazquez, Pedro A.
and
Perez, Alberto T.
2014.
Numerical simulation of annular electroconvection in a dielectric liquid induced by unipolar injection.
p.
1.
Wu, Jian
Vázquez, Pédro A.
Traoré, Philippe
and
Pérez, Alberto T.
2014.
Finite amplitude electroconvection induced by strong unipolar injection between two coaxial cylinders.
Physics of Fluids,
Vol. 26,
Issue. 12,
Wu, Jian
Traoré, Philippe
Pérez, Alberto T.
and
Zhang, Mengqi
2015.
Numerical analysis of the subcritical feature of electro-thermo-convection in a plane layer of dielectric liquid.
Physica D: Nonlinear Phenomena,
Vol. 311-312,
Issue. ,
p.
45.
Wu, Jian
and
Traoré, Philippe
2015.
A Finite-Volume Method for Electro-Thermoconvective Phenomena in a Plane Layer of Dielectric Liquid.
Numerical Heat Transfer, Part A: Applications,
Vol. 68,
Issue. 5,
p.
471.
Pankrat’eva, I. L.
and
Polyanskii, V. A.
2015.
Investigation of the mechanisms of the onset of instability in weakly conduction media in electric fields.
Fluid Dynamics,
Vol. 50,
Issue. 6,
p.
769.
Wu, Jian
Perez, Alberto T.
Traore, Philippe
and
Vazquez, Pedro A.
2015.
Complex flow patterns at the onset of annular electroconvection in a dielectric liquid subjected to an arbitrary unipolar injection.
IEEE Transactions on Dielectrics and Electrical Insulation,
Vol. 22,
Issue. 5,
p.
2637.
Wu, Jian
Traore, Philippe
Louste, Christophe
Dascalescu, Lucian
Tian, Fang-Bao
and
Perez, Alberto T.
2015.
Numerical Investigation of Electrohydrodynamic Plumes for Locally Enhanced Cooling in Dielectric Liquids.
IEEE Transactions on Industry Applications,
Vol. 51,
Issue. 1,
p.
669.
Traoré, P.
Wu, J.
and
Pérez, A.T.
2016.
Direct numerical simulation of the subcritical electroconvective instability in a dielectric liquid subjected to strong or weak unipolar injection.
European Journal of Mechanics - B/Fluids,
Vol. 59,
Issue. ,
p.
25.
Zhang, Mengqi
2016.
Weakly nonlinear stability analysis of subcritical electrohydrodynamic flow subject to strong unipolar injection.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
328.
Wang, Bo-Fu
and
Wen-Hann Sheu, Tony
2016.
Numerical investigation of electrohydrodynamic instability and bifurcation in a dielectric liquid subjected to unipolar injection.
Computers & Fluids,
Vol. 136,
Issue. ,
p.
1.
Kourmatzis, Agisilaos
and
Shrimpton, John S
2016.
Characteristics of electrohydrodynamic roll structures in laminar planar Couette flow.
Journal of Physics D: Applied Physics,
Vol. 49,
Issue. 4,
p.
045503.
Luo, Kang
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2016.
Lattice Boltzmann model for Coulomb-driven flows in dielectric liquids.
Physical Review E,
Vol. 93,
Issue. 2,
Luo, Kang
Wu, Jian
Yi, Hong-Liang
and
Tan, He-Ping
2018.
Three-dimensional finite amplitude electroconvection in dielectric liquids.
Physics of Fluids,
Vol. 30,
Issue. 2,
Guan, Yifei
and
Novosselov, Igor
2019.
Two relaxation time lattice Boltzmann method coupled to fast Fourier transform Poisson solver: Application to electroconvective flow.
Journal of Computational Physics,
Vol. 397,
Issue. ,
p.
108830.
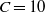 $C= 10$), the results look very similar for a given range of the mobility parameter
$C= 10$), the results look very similar for a given range of the mobility parameter 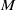 $M$; however, in the weak injection regime (
$M$; however, in the weak injection regime (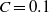 $C= 0. 1$), significant discrepancies are observed. The rich flow structures obtained with the NSC approach invalidate the use of the IVF approach in the weak injection regime.
$C= 0. 1$), significant discrepancies are observed. The rich flow structures obtained with the NSC approach invalidate the use of the IVF approach in the weak injection regime.