Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Imayama, Shintaro
Lingwood, R.J.
and
Alfredsson, P. Henrik
2014.
The turbulent rotating-disk boundary layer.
European Journal of Mechanics - B/Fluids,
Vol. 48,
Issue. ,
p.
245.
Appelquist, E.
Schlatter, P.
Alfredsson, P.H.
and
Lingwood, R.J.
2015.
Investigation of the Global Instability of the Rotating-disk Boundary Layer.
Procedia IUTAM,
Vol. 14,
Issue. ,
p.
321.
Appelquist, E.
Schlatter, P.
Alfredsson, P. H.
and
Lingwood, R. J.
2015.
Global linear instability of the rotating-disk flow investigated through simulations.
Journal of Fluid Mechanics,
Vol. 765,
Issue. ,
p.
612.
Lingwood, R. J.
and
Henrik Alfredsson, P.
2015.
Instabilities of the von Kármán Boundary Layer.
Applied Mechanics Reviews,
Vol. 67,
Issue. 3,
Imayama, Shintaro
Alfredsson, P. Henrik
and
Lingwood, R. J.
2016.
Experimental study of rotating-disk boundary-layer flow with surface roughness.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
5.
Alveroglu, B.
Segalini, A.
and
Garrett, S.J.
2016.
The effect of surface roughness on the convective instability of the BEK family of boundary-layer flows.
European Journal of Mechanics - B/Fluids,
Vol. 56,
Issue. ,
p.
178.
Appelquist, E.
Imayama, Shintaro
Alfredsson, P. Henrik
Schlatter, P.
and
Lingwood, R.J.
2016.
Linear disturbances in the rotating-disk flow: A comparison between results from simulations, experiments and theory.
European Journal of Mechanics - B/Fluids,
Vol. 55,
Issue. ,
p.
170.
Appelquist, E.
Schlatter, P.
Alfredsson, P. H.
and
Lingwood, R. J.
2016.
On the global nonlinear instability of the rotating-disk flow over a finite domain.
Journal of Fluid Mechanics,
Vol. 803,
Issue. ,
p.
332.
Ho, Joanna
Corke, Thomas C.
and
Matlis, Eric
2016.
Effect of wall suction on rotating disk absolute instability.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
704.
Griffiths, P.T.
Garrett, S.J.
Stephen, S.O.
and
Hussain, Z.
2017.
Quantifying non-Newtonian effects in rotating boundary-layer flows.
European Journal of Mechanics - B/Fluids,
Vol. 61,
Issue. ,
p.
304.
Munekata, Mizue
Utatsu, Takaomi
Yoshikawa, Hiroyuki
and
Okumura, Yasuhiro
2017.
Effects of Orbital Motion on the Velocity Field of Boundary Layer Flow over a Rotating Disk.
Open Journal of Fluid Dynamics,
Vol. 07,
Issue. 02,
p.
169.
Lee, Keunseob
Nishio, Yu
Izawa, Seiichiro
and
Fukunishi, Yu
2017.
Effects of location of excitation on the spiral vortices in the transitional region of a rotating-disk flow.
Physics of Fluids,
Vol. 29,
Issue. 8,
Segalini, Antonio
and
Garrett, Stephen J.
2017.
On the non-parallel instability of the rotating-sphere boundary layer.
Journal of Fluid Mechanics,
Vol. 818,
Issue. ,
p.
288.
Luo, Xia
Jedlicka, Sabrina S.
Jellison, Kristen L.
and
Schaffner, Donald W.
2017.
Role of Wall Shear Stress in Cryptosporidium parvum Oocyst Attachment to Environmental Biofilms.
Applied and Environmental Microbiology,
Vol. 83,
Issue. 24,
Arratia, Cristóbal
Mowlavi, Saviz
and
Gallaire, François
2018.
Absolute/convective secondary instabilities and the role of confinement in free shear layers.
Physical Review Fluids,
Vol. 3,
Issue. 5,
2018.
Gas Turbines.
p.
182.
Lee, K.
Nishio, Y.
Izawa, S.
and
Fukunishi, Y.
2018.
The effect of downstream turbulent region on the spiral vortex structures of a rotating-disk flow.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
274.
Yim, Eunok
Chomaz, J.-M.
Martinand, D.
and
Serre, E.
2018.
Transition to turbulence in the rotating disk boundary layer of a rotor–stator cavity.
Journal of Fluid Mechanics,
Vol. 848,
Issue. ,
p.
631.
Appelquist, E.
Schlatter, P.
Alfredsson, P. H.
and
Lingwood, R. J.
2018.
Transition to turbulence in the rotating-disk boundary-layer flow with stationary vortices.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
43.
Thomas, Christian
and
Davies, Christopher
2018.
On the impulse response and global instability development of the infinite rotating-disc boundary layer.
Journal of Fluid Mechanics,
Vol. 857,
Issue. ,
p.
239.
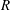 $R$, of
$R$, of  $\sim $510, i.e. at the onset of Lingwood’s (J. Fluid Mech., vol. 299, 1995, pp. 17–33) local absolute instability, and the growth of stationary vortices saturates at a Reynolds number of
$\sim $510, i.e. at the onset of Lingwood’s (J. Fluid Mech., vol. 299, 1995, pp. 17–33) local absolute instability, and the growth of stationary vortices saturates at a Reynolds number of 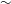 $\sim $550. The nonlinear saturation and subsequent turbulent breakdown of individual stationary vortices independently of their amplitudes, which vary azimuthally, seem to be determined by well-defined Reynolds numbers. We identify unstable travelling disturbances in our power spectra, which continue to grow, saturating at around
$\sim $550. The nonlinear saturation and subsequent turbulent breakdown of individual stationary vortices independently of their amplitudes, which vary azimuthally, seem to be determined by well-defined Reynolds numbers. We identify unstable travelling disturbances in our power spectra, which continue to grow, saturating at around 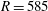 $R=585$, whereupon turbulent breakdown of the boundary layer ensues. The nonlinear saturation amplitude of the total disturbance field is approximately constant for all considered cases, i.e. different rotation rates and edge Reynolds numbers. We also identify a travelling secondary instability. Our results suggest that it is the travelling disturbances that are fundamentally important to the transition to turbulence for a clean disk, rather than the stationary vortices. Here, the results appear to show a primary nonlinear steep-fronted (travelling) global mode at the boundary between the local convectively and absolutely unstable regions, which develops nonlinearly interacting with the stationary vortices and which saturates and is unstable to a secondary instability. This leads to a rapid transition to turbulence outward of the primary front from approximately
$R=585$, whereupon turbulent breakdown of the boundary layer ensues. The nonlinear saturation amplitude of the total disturbance field is approximately constant for all considered cases, i.e. different rotation rates and edge Reynolds numbers. We also identify a travelling secondary instability. Our results suggest that it is the travelling disturbances that are fundamentally important to the transition to turbulence for a clean disk, rather than the stationary vortices. Here, the results appear to show a primary nonlinear steep-fronted (travelling) global mode at the boundary between the local convectively and absolutely unstable regions, which develops nonlinearly interacting with the stationary vortices and which saturates and is unstable to a secondary instability. This leads to a rapid transition to turbulence outward of the primary front from approximately 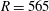 $R=565$ to 590 and to a fully turbulent boundary layer above 650.
$R=565$ to 590 and to a fully turbulent boundary layer above 650.