Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T13:17:54.539Z Has data issue: false hasContentIssue false
  • English
  • Français

On the influence of Sommerfeld’s radiation boundary condition on the propagation direction of oblique modes in streamwise corner flow

Published online by Cambridge University Press:  20 October 2016

Jennifer Staudenmeyer ,
Oliver T. Schmidt  and
Ulrich Rist
Jennifer Staudenmeyer*
Affiliation:
Institut für Aerodynamik und Gasdynamik, Universität Stuttgart, Pfaffenwaldring 21, 70569 Stuttgart, Germany
Oliver T. Schmidt
Affiliation:
Department of Mechanical and Civil Engineering, California Institute of Technology, Pasadena, CA 91125, USA
Ulrich Rist
Affiliation:
Institut für Aerodynamik und Gasdynamik, Universität Stuttgart, Pfaffenwaldring 21, 70569 Stuttgart, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear stability of a laminar boundary-layer flow in a streamwise corner can only be treated with an ansatz that considers two-dimensional eigenfunctions with inhomogeneous boundary conditions in cross-flow directions. It is common practice to use Sommerfeld’s radiation condition with a certain wavenumber $\unicode[STIX]{x1D6FD}$ at the lateral domains of the integration domain which are at the same time the far-field domains for each wall. So far, this radiation condition has been exclusively used in a ‘symmetrical’ way, i.e. with the same 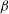$\unicode[STIX]{x1D6FD}$ on either far-field boundary plane. This has led to wave patterns that either enter or leave the corner region from the lateral sides for 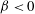$\unicode[STIX]{x1D6FD}<0$ or 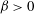$\unicode[STIX]{x1D6FD}>0$ respectively. Here, an ‘asymmetric’ use of Sommerfeld’s radiation condition is suggested, i.e. 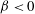$\unicode[STIX]{x1D6FD}<0$ on one far side of the corner and 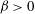$\unicode[STIX]{x1D6FD}>0$ on the other. With this modification, waves enter the corner area from one side and leave it through the other, i.e. they travel obliquely through the corner. In contrast to before, their amplification rate is always symmetric with respect to 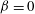$\unicode[STIX]{x1D6FD}=0$ and there is no amplification-rate increase or decrease due to information that either continuously enters the corner from both sides or continuously leaves it through the far sides. The present analysis also shows that the inviscid corner modes are unaffected by the parameters of the far-field radiation boundary conditions. Nevertheless, superposition of two oppositely running single waves obtained by the modified application of the radiation condition leads to a similar wave pattern to that in the case with 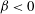$\unicode[STIX]{x1D6FD}<0$ on both sides; however, with a slightly smaller amplification rate and a strictly streamwise propagation direction.

JFM classification

Boundary Layers: Boundary layer stability Boundary Layers: Boundary Layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 807 , 25 November 2016 , R3
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alizard, F., Robinet, J.-C. & Rist, U. 2010 Sensitivity analysis of a streamwise corner flow. Phys. Fluids 22 (1), 014103.Google Scholar
Balachandar, S. & Malik, M. R. 1995 Inviscid instability of streamwise corner flow. J. Fluid Mech. 282, 187–201.Google Scholar
Barclay, W. H. & Ridha, A. H. 1980 Flow in streamwise corners of arbitrary angle. AIAA J. 18 (12), 1413–1420.CrossRefGoogle Scholar
Galionis, I. & Hall, P. 2005 Spatial stability of the incompressible corner flow. Theor. Comput. Fluid Dyn. 19 (2), 77–113.Google Scholar
Ghia, K. N. 1975 Incompressible streamwise flow along an unbounded corner. AIAA J. 13 (7), 902–907.Google Scholar
Ghia, K. N. & Davis, R. T. 1974 A study of compressible potential and asymptotic viscous flows for corner region. AIAA J. 12 (3), 355–359.Google Scholar
Lin, R. S., Wang, W. P. & Malik, M. R. 1996 Linear stability of incompressible viscous flow along a corner. ASME-PUBLICATIONS-FED 237, 633–638.Google Scholar
Mikhail, A. G. & Ghia, K. N. 1978 Viscous compressible flow in the boundary region of an axial corner. AIAA J. 16 (9), 931–939.Google Scholar
Pal, A. & Rubin, S. G. 1971 Asymptotic features of viscous flow along a corner. Q. Appl. Maths 29, 91–108.CrossRefGoogle Scholar
Parker, S. J. & Balachandar, S. 1999 Viscous and inviscid instabilities of flow along a streamwise corner. Theor. Comput. Fluid Dyn. 13 (4), 231–270.Google Scholar
Ridha, A. 1992 On the dual solutions associated with boundary-layer equations in a corner. J. Engng Maths 26 (4), 525–537.Google Scholar
Rubin, S. G. 1966 Incompressible flow along a corner. J. Fluid Mech. 26 (1), 97–110.Google Scholar
Rubin, S. G. & Grossman, B. 1971 Viscous flow along a corner: numerical solution of corner layer equations. Q. Appl. Maths 29, 169–186.Google Scholar
Schmidt, O. T.2014 Numerical investigations of instability and transition in streamwise corner-flows. PhD thesis, University of Stuttgart.Google Scholar
Schmidt, O. T. & Rist, U. 2011 Linear stability of compressible flow in a streamwise corner. J. Fluid Mech. 688, 569–590.Google Scholar
Tannehill, J. C., Anderson, D. A. & Pletcher, R. H. 1997 Computational Fluid Mechanics and Heat Transfer, 2nd edn. Taylor & Francis.Google Scholar
Weinberg, B. C. & Rubin, S. G. 1972 Compressible corner flow. J. Fluid Mech. 56 (4), 753–774.Google Scholar