Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T13:42:15.933Z Has data issue: false hasContentIssue false
  • English
  • Français

On the inertial wave activity during spin-down in a rapidly rotating penny shaped cylinder: a reduced model

Published online by Cambridge University Press:  06 February 2020

L. Oruba Open the ORCID record for L. Oruba [Opens in a new window] ,
A. M. Soward Open the ORCID record for A. M. Soward [Opens in a new window]  and
E. Dormy Open the ORCID record for E. Dormy [Opens in a new window]
L. Oruba*
Affiliation:
Laboratoire Atmosphères Milieux Observations Spatiales (LATMOS/IPSL), Sorbonne Université, UVSQ, CNRS, Paris, France
A. M. Soward*
Affiliation:
School of Mathematics, Statistics and Physics, Newcastle University, Newcastle upon TyneNE1 7RU, UK
E. Dormy*
Affiliation:
Département de Mathématiques et Applications, UMR-8553, École Normale Supérieure, CNRS, PSL University, 75005Paris, France
*
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

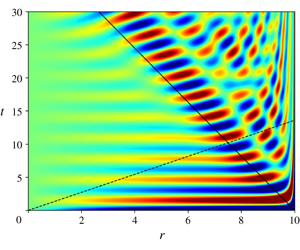
In a previous paper, Oruba et al. (J. Fluid Mech., vol. 818, 2017, pp. 205–240) considered the ‘primary’ quasi-steady geostrophic (QG) motion of a constant density fluid of viscosity $\unicode[STIX]{x1D708}$ that occurs during linear spin-down in a cylindrical container of radius $r^{\dagger }=L$ and height $z^{\dagger }=H$, rotating rapidly (angular velocity $\unicode[STIX]{x1D6FA}$) about its axis of symmetry subject to mixed rigid and stress-free boundary conditions for the case $L=H$. Here, Direct numerical simulation at large $L=10H$ and Ekman numbers $E=\unicode[STIX]{x1D708}/H^{2}\unicode[STIX]{x1D6FA}$ in the range $=10^{-3}{-}10^{-7}$ reveals inertial wave activity on the spin-down time scale $E^{-1/2}\unicode[STIX]{x1D6FA}^{-1}$. Our analytic study, based on $E\ll 1$, builds on the results of Greenspan & Howard (J. Fluid Mech., vol. 17, 1963, pp. 385–404) for an infinite plane layer $L\rightarrow \infty$. In addition to QG spin-down, they identify a ‘secondary’ set of quasi-maximum frequency $\unicode[STIX]{x1D714}^{\dagger }\rightarrow 2\unicode[STIX]{x1D6FA}$ (MF) inertial waves, which is a manifestation of the transient Ekman layer, decaying algebraically $\propto 1/\surd \,t^{\dagger }$. Here, we acknowledge that the blocking of the meridional parts of both the primary-QG and the secondary-MF spin-down flows by the lateral boundary $r^{\dagger }=L$ provides a trigger for other inertial waves. As we only investigate the response to the primary QG-trigger, we call the model ‘reduced’ and for that only inertial waves with frequencies $\unicode[STIX]{x1D714}^{\dagger }<2\unicode[STIX]{x1D6FA}$ are triggered. We explain the ensuing organised inertial wave structure via an analytic study of the thin disc limit $L\gg H$ restricted to the region $L-r^{\dagger }=O(H)$ far from the axis, where we make a Cartesian approximation of the cylindrical geometry. Other than identifying a small scale fan structure emanating from the corner $[r^{\dagger },z^{\dagger }]=[L,0]$, we show that inertial waves, on the gap length scale $H$, radiated (wave energy flux) away from the outer boundary $r^{\dagger }=L$ (but propagating with a phase velocity towards it) reach a distance determined by the mode with the fastest group velocity.

JFM classification

Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 888 , 10 April 2020 , A9
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 2010 NIST Handbook of Mathematical Functions (ed. Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W.). CUP. Available at: http://dlmf.nist.gov/.Google Scholar
Atkinson, J. W., Davidson, P. A. & Perry, J. E. G. 2019 Dynamics of a trapped vortex in rotating convection. Phys. Rev. Fluids 4, 074701.CrossRefGoogle Scholar
Brunet, M., Dauxois, T. & Cortet, P.-P. 2019 Linear and nonlinear regimes of an inertial wave attractor. Phys. Rev. Fluids 4, 034801.CrossRefGoogle Scholar
Calabretto, S. A. W., Denier, J. P. & Mattner, T. W. 2018 The transient development of the flow in an impulsively rotated annular container. Theor. Comput. Fluid Dyn. 32, 821–845.CrossRefGoogle Scholar
Cederlöf, U. 1988 Free-surface effects on spin-up. J. Fluid Mech. 187, 395–407.CrossRefGoogle Scholar
Chelton, D. B., Schlax, M. G. & Samelson, R. M. 2011 Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 91, 167–216.CrossRefGoogle Scholar
Chen, S., Lu, Y., Li, W. & Wen, Z. 2015 Identification and analysis of high-frequency oscillations in the eyewall of tropical cyclones. Adv. Atmos. Sci. 32, 624–634.CrossRefGoogle Scholar
Chester, C., Friedman, B. & Ursell, F. 1957 An extension of the method of steepest descents. Proc. Camb. Phil. Soc. 53, 599–611.CrossRefGoogle Scholar
Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.CrossRefGoogle Scholar
Dolzhanskii, F. V., Krymov, V. A. & Manin, Y. 1992 Self-similar spin-up and spin-down in a cylinder of small ratio of height to diameter. J. Fluid Mech. 234, 473–486.CrossRefGoogle Scholar
Duck, P. W. & Foster, M. R. 2001 Spin-up of homogeneous and stratified fluids. Annu. Rev. Fluid Mech. 33, 231–263.CrossRefGoogle Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F. & Tricomi, F. G. 1954 Tables of Integral Transforms (Director A. Bateman), vol. I. McGraw-Hill Book Company.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series, and Products (ed. Jeffrey, A. & Zwillinger, D.). Elsevier.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.CrossRefGoogle Scholar
Harlow, F. H. & Stein, L. R. 1974 Structural analysis of tornado-like vortices. J. Atmos. Sci. 31, 2081–2098.2.0.CO;2>CrossRefGoogle Scholar
Heyvaerts, J. & Priest, E. R. 1983 Coronal heating by phase-mixed shear Alfvén waves. Astron. Astrophys. 117, 220–234.Google Scholar
Jouve, L. & Ogilvie, G. I. 2014 Direct numerical simulations of an inertial wave attractor in linear and nonlinear regimes. J. Fluid Mech. 745, 223–250.CrossRefGoogle Scholar
Kerswell, R. R. & Barenghi, C. F. 1995 On the viscous decay rates of inertial waves in a rotating circular cylinder. J. Fluid Mech. 285, 203–214.CrossRefGoogle Scholar
Klein, M., Seelig, T., Kurgansky, M. V., Ghasemi V., A., Borcia, I. D., Will, A., Schaller, E., Egbers, C. & Harlander, U. 2014 Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder. J. Fluid Mech. 751, 255–297.CrossRefGoogle Scholar
Li, L., Patterson, M. D., Zhang, K. & Kerswell, R. R. 2012 Spin-up and spin-down in a half cone: a pathological situation or not? Phys. Fluids 24, 116601.CrossRefGoogle ScholarPubMed
Mason, R. M. & Kerswell, R. R. 2002 Chaotic dynamics in a strained rotating flow: a precessing plane fluid layer. J. Fluid Mech. 471, 71–106.CrossRefGoogle Scholar
Oruba, L., Davidson, P. A. & Dormy, E. 2017 Eye formation in rotating convection. J. Fluid Mech. 812, 890–904.CrossRefGoogle Scholar
Oruba, L., Davidson, P. A. & Dormy, E. 2018 Formation of eyes in large-scale cyclonic vortices. Phys. Rev. Fluids 3, 013502.CrossRefGoogle Scholar
Oruba, L., Soward, A. M. & Dormy, E. 2017 Spin-down in a rapidly rotating cylinder container with mixed rigid and stress-free boundary conditions. J. Fluid Mech. 818, 205–240.CrossRefGoogle Scholar
Persing, J., Montgomery, M. T., Smith, R. K. & McWilliams, J. C. 2015 On the realism of quasi steady-state hurricanes. Q. J. R. Meteorol. Soc. 141, 1–14.Google Scholar
Scott, J. F. 2014 Wave turbulence in a rotating channel. J. Fluid Mech. 741, 316–349.CrossRefGoogle Scholar
Ursell, U. 1960 On Kelvin’s ship-wave pattern. J. Fluid Mech. 8, 418–431.CrossRefGoogle Scholar
Watson, G. N. 1966 A Treatise on the Theory of Bessel Functions. Cambridge University Press.Google Scholar
Zhang, K. & Liao, X. 2008 On the initial-value problem in a rotating circular cylinder. J. Fluid Mech. 610, 425–443.CrossRefGoogle Scholar
Zhang, K. & Liao, X. 2017 Theory and Modeling of Rotating Fluids: Convection, Inertial Waves and Precession. Cambridge University Press.CrossRefGoogle Scholar

Oruba et al. supplementary movie 1

{\it Movie 1}\\ This movie shows the $\chi$-contours in the case $\Ek=10^{-3}$, as a function of time: (a) the direct numerical simulations $\Ek^{-1/2}\chi_{\tDNS}$ (colour scale from -0.3 to 0.3); (b) the filtered DNS, with the geostrophic flow substracted $\chi_{\tFNS}$ (colour scale from -0.1 to 0.1); (c) the analytic solutions $\chi_{\tIW}$ (colour scale from -0.1 to 0.1).\\

Download Oruba et al. supplementary movie 1(Video)
Video 3.1 MB

Oruba et al. supplementary movie 2

{\it Movie 2}\\ This movie shows the $v$-contours in the case $\Ek=10^{-3}$, as a function of time: (a) the direct numerical simulations $\Ek^{-1/2}v_{\tDNS}$ (colour scale from -30 to 30); (b) the filtered DNS, with the geostrophic flow substracted $v_{\tFNS}$ (colour scale from -0.5 to 0.5); (c) the analytic solutions $v_{\tIW}$ (colour scale from -0.5 to 0.5).\\

Download Oruba et al. supplementary movie 2(Video)
Video 2.8 MB

Oruba et al. supplementary movie 3

{\it Movie 3}\\ This movie shows the $\chi$-contours in the case $\Ek=10^{-5}$, as a function of time: (a) the direct numerical simulations $\Ek^{-1/2}\chi_{\tDNS}$ (colour scale from -0.3 to 0.3); (b) the filtered DNS, with the geostrophic flow substracted $\chi_{\tFNS}$ (colour scale from -0.1 to 0.1); (c) the analytic solutions $\chi_{\tIW}$ (colour scale from -0.1 to 0.1).\\

Download Oruba et al. supplementary movie 3(Video)
Video 4.5 MB

Oruba et al. supplementary movie 4

{\it Movie 4}\\ This movie shows the $v$-contours in the case $\Ek=10^{-5}$, as a function of time: (a) the direct numerical simulations $\Ek^{-1/2}v_{\tDNS}$ (colour scale from -30 to 30); (b) the filtered DNS, with the geostrophic flow substracted $v_{\tFNS}$ (colour scale from -0.5 to 0.5); (c) the analytic solutions $v_{\tIW}$ (colour scale from -0.5 to 0.5).\\

Download Oruba et al. supplementary movie 4(Video)
Video 3 MB

Oruba et al. supplementary movie 5

{\it Movie 5}\\ This movie shows the $\chi$-contours in the case $\Ek=10^{-7}$, as a function of time: (a) the direct numerical simulations $\Ek^{-1/2}\chi_{DNS}$ (colour scale from -0.3 to 0.3); (b) the filtered DNS, with the geostrophic flow substracted $\chi_{FNS}$ (colour scale from -0.1 to 0.1); (c) the analytic solutions $\chi_{IW}$ (colour scale from -0.1 to 0.1).\\

Download Oruba et al. supplementary movie 5(Video)
Video 4.4 MB

Oruba et al. supplementary movie 6

{\it Movie 6}\\ This movie shows the $v$-contours in the case $\Ek=10^{-7}$, as a function of time: (a) the direct numerical simulations $\Ek^{-1/2}v_{\tDNS}$ (colour scale from -30 to 30); (b) the filtered DNS, with the geostrophic flow substracted $v_{\tFNS}$ (colour scale from -0.5 to 0.5); (c) the analytic solutions $v_{\tIW}$ (colour scale from -0.5 to 0.5).\\

Download Oruba et al. supplementary movie 6(Video)
Video 2.9 MB

Oruba et al. supplementary movie 7

{\it Movie 7}\\ This movie shows the meridional speed $E^{-1/2}\sqrt{u^2+w^2}=r^{-1}\bigl|\bfnabla(r\chi)\bigr|$, as a function of time. Respectively, the panels show results for: ($a$)--($c$) the filtered DNS $\chi_\tFNS$, when ($a$) $E=10^{-3}$, ($b$) $E=10^{-5}$, ($c$) $E=10^{-7}$; ($d$) the analytic $\chi^{\rm{wave}}$ in the limit $E\downarrow 0$; ($e$) the full DNS $E^{-1/2}\chi_\tDNS$ when $E=10^{-7}$ (colour scale from $0$ to $3$).

Download Oruba et al. supplementary movie 7(Video)
Video 907.9 KB
Supplementary material: PDF

Oruba et al. supplementary material

Supplementary Data

Download Oruba et al. supplementary material(PDF)
PDF 40.7 KB