Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T03:54:20.187Z Has data issue: false hasContentIssue false
  • English
  • Français

On the formation of axial corner vortices during spin-up in a cylinder of square cross-section

Published online by Cambridge University Press:  05 May 2015

R. J. Munro ,
R. E. Hewitt  and
M. R. Foster
R. J. Munro*
Affiliation:
Faculty of Engineering, University of Nottingham, Nottingham NG7 2RD, UK
R. E. Hewitt
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK
M. R. Foster
Affiliation:
Department of Mathematical Sciences, Rensselaer Polytechnic Institute, Troy, NY 12180, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present experimental and theoretical results for the adjustment of a fluid (homogeneous or linearly stratified), which is initially rotating as a solid body with angular frequency 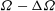${\it\Omega}-{\rm\Delta}{\it\Omega}$, to a nonlinear increase 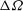${\rm\Delta}{\it\Omega}$ in the angular frequency of all bounding surfaces. The fluid is contained in a cylinder of square cross-section which is aligned centrally along the rotation axis, and we focus on the 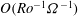$O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$ time scale, where 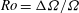$\mathit{Ro}={\rm\Delta}{\it\Omega}/{\it\Omega}$ is the Rossby number. The flow development is shown to be dominated by unsteady separation of a viscous sidewall layer, leading to an eruption of vorticity that becomes trapped in the four vertical corners of the container. The longer-time evolution on the standard ‘spin-up’ time scale, 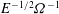$E^{-1/2}{\it\Omega}^{-1}$ (where 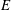$E$ is the associated Ekman number), has been described in detail for this geometry by Foster & Munro (J. Fluid Mech., vol. 712, 2012, pp. 7–40), but only for small changes in the container’s rotation rate (i.e. 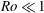$\mathit{Ro}\ll 1$). In the linear case, for 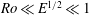$\mathit{Ro}\ll E^{1/2}\ll 1$, there is no sidewall separation. In the present investigation we focus on the fully nonlinear problem, 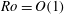$\mathit{Ro}=O(1)$, for which the sidewall viscous layers are Prandtl boundary layers and (somewhat unusually) periodic around the container’s circumference. Some care is required in the corners of the container, but we show that the sidewall boundary layer breaks down (separates) shortly after an impulsive change in rotation rate. These theoretical boundary-layer results are compared with two-dimensional Navier–Stokes results which capture the eruption of vorticity, and these are in turn compared to laboratory observations and data. The experiments show that when the Burger number, 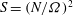$S=(N/{\it\Omega})^{2}$ (where 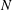$N$ is the buoyancy frequency), is relatively large – corresponding to a strongly stratified fluid – the flow remains (horizontally) two-dimensional on the 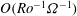$O(\mathit{Ro}^{-1}{\it\Omega}^{-1})$ time scale, and good quantitative predictions can be made by a two-dimensional theory. As 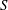$S$ was reduced in the experiments, three-dimensional effects were observed to become important in the core of each corner vortex, on this time scale, but only after the breakdown of the sidewall layers.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 246 - 271
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benton, E. R. & Clark, A. 1974 Spin-up. Annu. Rev. Fluid Mech. 6, 257–280.Google Scholar
Cebeci, T. 1986 Unsteady boundary layers with an intelligent numerical scheme. J. Fluid Mech. 163, 129–140.Google Scholar
Dalziel, S. B.2006 Digiflow user guide. Available at: http://www.damtp.cam.ac.uk/lab/digiflow/.Google Scholar
Duck, P. W. & Foster, M. R. 2001 Spin-up of homogeneous and stratified fluids. Annu. Rev. Fluid Mech. 33, 231–263.CrossRefGoogle Scholar
Duck, P. W., Foster, M. R. & Hewitt, R. E. 1997 On the boundary layer arising in the spin-up of a stratified fluid in a container with sloping walls. J. Fluid Mech. 335, 233–259.Google Scholar
Economidou, M. & Hunt, G. R. 2009 Density stratified environments: the double-tank method. Exp. Fluids 46, 453–466.Google Scholar
Foster, M. R. & Munro, R. J. 2012 The linear spin-up of a stratified, rotating fluid in a square cylinder. J. Fluid Mech. 712, 7–40.CrossRefGoogle Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.Google Scholar
Heil, M. & Hazel, A. L. 2006 An object-oriented multi-physics finite-element library. In Fluid-Structure Interaction (ed. Schafer, M. & Bungartz, H.-J.), Lecture Notes on Computational Science and Engineering, pp. 19–49. Springer, oomph-lib is available as open-source software at http://www.oomph-lib.org.Google Scholar
Hewitt, R. E., Davies, P. A., Duck, P. W. & Foster, M. R. 1999 Spin-up of stratified rotating flows at large Schmidt number: experiment and theory. J. Fluid Mech. 389, 169–207.Google Scholar
Hewitt, R. E., Foster, M. R. & Davies, P. A. 2001 Spin-up of a two-layer rotating stratified fluid in a variable-depth container. J. Fluid Mech. 438, 379–407.Google Scholar
Hewitt, R. E., Hazel, A. L., Clarke, R. J. & Denier, J. P. 2011 Unsteady flow in a rotating torus after a sudden change in rotation rate. J. Fluid Mech. 688, 88–119.Google Scholar
Koumoutsakos, P. & Leonard, A. 1995 High-resolution simulations of the flow around an impulsively started cylinder using vortex methods. J. Fluid Mech. 296, 1–38.Google Scholar
MacCready, P. & Rhines, P. B. 1991 Buoyant inhibition of Ekman transport on a slope and its effect on stratified spin-up. J. Fluid Mech. 223, 631–661.Google Scholar
Munro, R. J., Foster, M. R. & Davies, P. A. 2010 Instabilities in the spin-up of a rotating, stratified fluid. Phys. Fluids 22 (5), 054108.Google Scholar
Smirnov, S. A., Baines, P. G., Boyer, D. L., Voropayev, S. I. & Srdic-Mitrovic, A. N. 2005 Long-time evolution of linearly stratified spin-up flows in axisymmetric geometries. Phys. Fluids 17 (1), 016601.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.Google Scholar
Thomas, L. N. & Rhines, P. B. 2002 Nonlinear stratified spin-up. J. Fluid Mech. 473, 211–244.Google Scholar
van de Konijnenberg, J. A. & van Heijst, G. J. F. 1997 Free-surface effects on spin-up in a rectangular tank. J. Fluid Mech. 334, 189–210.CrossRefGoogle Scholar
van Heijst, G. J. F. 1989 Spin-up phenomena in non-axisymmetric containers. J. Fluid Mech. 206, 171–191.Google Scholar
van Heijst, G. J. F., Davies, P. A. & Davis, R. G. 1990 Spin-up in a rectangular container. Phys. Fluids A 2, 150–159.Google Scholar
Walin, G. 1969 Some aspects of time-dependent motion of a stratified rotating fluid. J. Fluid Mech. 36 (2), 289–307.Google Scholar
Weidman, P. D. 1976 On the spin-up and spin-down of a rotating fluid. Part 1. Extending the Wedemeyer model. J. Fluid Mech. 77 (4), 685–708.Google Scholar