Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T14:05:14.898Z Has data issue: false hasContentIssue false
  • English
  • Français

On the flow and coherent structures generated by a circular array of rigid emerged cylinders placed in an open channel with flat and deformed bed

Published online by Cambridge University Press:  13 October 2017

Wen-Yi Chang ,
George Constantinescu Open the ORCID record for George Constantinescu [Opens in a new window]  and
Whey Fone Tsai
Wen-Yi Chang
Affiliation:
National Center for High Performance Computing, National Applied Research Laboratories, Hsinchu, 30076Taiwan
George Constantinescu*
Affiliation:
Department of Civil and Environmental Engineering, The University of Iowa, Iowa City, IA 52242, USA
Whey Fone Tsai
Affiliation:
National Center for High Performance Computing, National Applied Research Laboratories, Hsinchu, 30076Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow and the turbulence structure generated by a circular porous cylinder of diameter 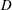$D$ containing solid cylinders of diameter 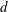$d$ placed in an open channel of depth 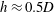$h\approx 0.5D$ are investigated using eddy-resolving simulations which resolve the wakes past the individual solid cylinders in the array. The solid cylinders extend from the bed through the water surface. This geometrical set-up is directly relevant to understand the physics of flow past an emerged patch of aquatic vegetation developing in a river channel or over its floodplain. Simulations are conducted with different solid volume fractions (SVFs) of the porous cylinder (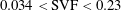$0.034<\text{SVF}<0.23$), relative diameters of the solid cylinders (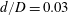$d/D=0.03$ and 0.06) and with flat and equilibrium scour bathymetry corresponding to the start and respectively the end of the erosion and deposition process. Comparison with the limiting case of a solid cylinder (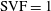$\text{SVF}=1$) is also discussed. The bed shear stress distributions and the turbulent flow fields are used to explain the sediment erosion mechanisms inside and around the porous cylinder. Simulations of the flat-bed cases reveal that for sufficiently large SVF values (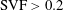$\text{SVF}>0.2$), necklace vortices form around the upstream face of the cylinder, the downflow penetrates partially inside the porous cylinder and a region of strong flow acceleration forms on the sides of the porous cylinder. These flow features are used to explain the development of scour around high-SVF porous cylinders. The effects of the SVF and 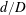$d/D$ on generating ‘corridors’ of strong flow acceleration in between the solid cylinders and energetic eddies in the wake of these cylinders are discussed, as these flow features control the amplification of the bed shear stress inside the porous cylinder. Simulations results are also used to quantify the time-averaged drag forces on the cylinders in the array, to identify the regions where these forces are comparable to those induced on an isolated cylinder and the percentage of cylinders in the array subject to relatively large mean drag forces. A logarithmic decrease of the mean time-averaged streamwise drag coefficient of the solid cylinders, 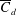$\overline{C}_{d}$, with increasing non-dimensional frontal area per unit volume of the porous cylinder, 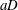$aD$, is observed. Behind the cylinder, the eddies shed in the separated shear layers (SSLs) of the porous cylinder, and, for sufficiently large SVFs, the von Kármán wake billows are the main coherent structures responsible for the amplification of the bed shear stress and sediment entrainment. This paper also analyses the vertical non-uniformity of the mean flow and turbulent kinetic energy, and discusses how the SVF and bathymetry affect the spatial extent of the wake region (e.g. length of the SSLs and steady wake, total wake length) and other relevant variables (e.g. strength of the bleeding flow, dominant wake frequencies, turbulence amplification in the near wake). For the relatively shallow flow conditions (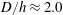$D/h\approx 2.0$) considered, the simulation results show that the antisymmetric (von Kármán) shedding of wake billows behind the porous cylinder is greatly weakened once equilibrium scour conditions are approached. Comparison with data from laboratory experiments and from 3-D and 2-D simulations conducted for long porous cylinders (no bed) is also discussed.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: River dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 1 - 40
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akilli, H. & Rockwell, D. 2002 Vortex formation from a cylinder in shallow water. Phys. Fluids 14 (9), 2957–2967.Google Scholar
Barry, N., Burton, D. & Sheridan, J. 2015 Aerodynamic drag interactions between cyclists in a team pursuit. Sports Engng 18 (2), 93–103.CrossRefGoogle Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.Google Scholar
Bennett, S. J., Pirim, T. & Barkdoll, B. D. 2002 Using simulated emergent vegetation to alter stream flow direction within a straight experimental channel. Geomorphology 44, 115–126.Google Scholar
Bennett, S. J., Wu, W., Alonso, C. V. & Wang, S. S. 2008 Modelling fluvial response to in-stream woody vegetation: implications for stream corridor restoration. Earth Surf. Process. Landf. 33, 890–909.CrossRefGoogle Scholar
Castro, I. P. 1971 Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 46, 599–609.CrossRefGoogle Scholar
Chang, K., Constantinescu, G. & Park, S. O. 2007 Assessment of predictive capabilities of detached eddy simulation to simulate flow and mass transport past open cavities. Trans ASME J. Fluids Engng 129 (11), 1372–1383.CrossRefGoogle Scholar
Chang, K. S. & Constantinescu, G. 2015 Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders. J. Fluid Mech. 776, 161–199.CrossRefGoogle Scholar
Chen, D. & Jirka, G. H. 1995 Experimental study of plane turbulent wakes in a shallow water layer. Fluid Dyn. Res. 16, 11–41.Google Scholar
Chen, Z., Ortiz, A., Zong, L. & Nepf, H. 2012 The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 48, W09517.Google Scholar
Constantinescu, G. 2014 LES of lock-exchange compositional gravity currents: A brief review of some recent results. Environ. Fluid Mech. 14, 295–317.Google Scholar
Constantinescu, G. & Squires, K. D. 2004 Numerical investigation of the flow over a sphere in the subcritical and supercritical regimes. Phys. Fluids 16 (5), 1449–1467.Google Scholar
Constantinescu, G. S., Miyawaki, S., Rhoads, B., Sukhodolov, A. & Kirkil, G. 2011 Structure of turbulent flow at a river confluence with momentum and velocity ratios close to 1: Insights from an eddy-resolving numerical simulation. Water Resour. Res. 47, W05507.Google Scholar
Constantinescu, G., Miyawaki, S., Rhoads, B. & Sukhodolov, A. 2012 Numerical analysis of the effect of momentum ratio on the dynamics and sediment entrainment capacity of coherent flow structures at a stream confluence. J. Geophys. Res. 117, F04028.Google Scholar
Cuenot, B., Magnaudet, J. & Spennato, B. S. 1997 The effects of slightly soluble surfactants on the flow around a spherical bubble. J. Fluid Mech. 339, 25–53.Google Scholar
Cui, J. & Neary, V. 2008 LES study of turbulent flows with submerged vegetation. J. Hydraul. Res. 46, 307–316.CrossRefGoogle Scholar
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P., Verboven, P., Nicolai, B. & Carmeliet, J. 2013 Cyclist drag in team pursuit: influence of cyclist sequence, stature and arm spacing. Trans. ASME J. Biomech. Engng 136, 011005.Google Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1, N11.Google Scholar
Follett, E. & Nepf, H. 2012 Sediment patterns near a model patch of reedy emergent vegetation. Geomorphology 179, 141–151.Google Scholar
Furukawa, K., Wolanski, E. & Mueller, H. 1997 Currents and sediment transport in mangrove forests. Estuar. Coast. Shelf Sci. 44, 301–310.Google Scholar
Garcia, M., Lopez, F., Dunn, C. & Alonso, C. V. 2004 Flow, turbulence, and resistance in a flume with simulated vegetation. In Riparian Vegetation and Fluvial Geomorphology (ed. Bennett, S. J. & Simon, A.), pp. 11–27. AGU.Google Scholar
Hansen, R. P. & Forsythe, J. R.2003. Large and detached eddy simulations of a circular cylinder using unstructured grids. AIAA Paper 2003-0775.CrossRefGoogle Scholar
Huang, Z. & Keffer, J. F. 1996 Development of structure within the turbulent wake of a porous body. Part 1. The initial formation region. J. Fluid Mech. 329, 103–115.CrossRefGoogle Scholar
Ingram, G. R. & Chu, V. H. 1987 Flow around islands in Rupert Bay: an investigation of the bottom friction effect. J. Geophys. Res. Atmos. 92 (C13), 521–533.Google Scholar
Jamali, M., Zhang, X. & Nepf, H. 2008 Exchange flow between a canopy and open water. J. Fluid Mech. 611, 237–254.CrossRefGoogle Scholar
Keylock, C. J., Constantinescu, S. G. & Hardy, R. J. 2012 The application of computational fluid dynamics to natural river channels: eddy resolving versus mean flow approaches. Geomorphology 179, 1–20.Google Scholar
King, A. T., Tinoco, R. O. & Cowen, E. A. 2012 A k–𝜀 turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 701, 1–39.Google Scholar
Kirkil, G. & Constantinescu, G. 2009 Nature of flow and turbulence structure around an in-stream vertical plate in a shallow channel and the implications for sediment erosion. Water Resour. Res. 45, W06412.CrossRefGoogle Scholar
Kirkil, G. & Constantinescu, G. 2010 Flow and turbulence structure around an in-stream rectangular cylinder with scour hole. Water Resour. Res. 46, W11549.CrossRefGoogle Scholar
Kirkil, G. & Constantinescu, G. 2012 The laminar necklace vortex system and wake structure in a shallow channel flow past a bottom-mounted circular cylinder. Phys. Fluids 24, 073602.Google Scholar
Kirkil, G. & Constantinescu, G. 2015 Effects of cylinder Reynolds number on the turbulent horseshoe vortex system and near wake of a surface-mounted circular cylinder. Phys. Fluids 27, 075102.Google Scholar
Kirkil, G., Constantinescu, G. & Ettema, R. 2009 DES investigation of turbulence and sediment transport at a circular pier with scour hole. ASCE J. Hydraul. Engng 135 (11), 888–901.Google Scholar
Koken, M. & Constantinescu, G. 2009 An investigation of the dynamics of coherent structures in a turbulent channel flow with a vertical sidewall obstruction. Phys. Fluids 21, 085104.Google Scholar
Koken, M., Constantinescu, G. & Blanckaert, K. 2013 Hydrodynamic processes, sediment erosion mechanisms, and Reynolds-number-induced scale effects in an open channel bend of strong curvature with flat bathymetry. J. Geophys. Res. Earth Surf. 118, 2308–2324.Google Scholar
Liu, D., Diplas, P., Fairbanks, J. D. & Hodges, C. C. 2008 An experimental study of flow through rigid vegetation. J. Geophys. Res. Earth Sci. 113, 1–16.Google Scholar
Marakoes, K. & Turner, J. 2006 Vortex generation in the cross flow around a cylinder attached to an end-wall. Opt. Laser Technol. 38 (4–6), 277–285.Google Scholar
Maza, M., Lara, J. L. & Losada, I. J. 2015 Tsunami wave interaction with mangrove forests: a 3-D numerical approach. Coast. Engng 98, 33–54.Google Scholar
Miller, M. C., McCave, I. N. & Komar, P. D. 1977 Threshold of sediment motion under unidirectional currents. Sedimentology 24, 507–527.Google Scholar
Neary, V. S., Constantinescu, S. G., Benett, S. J. & Diplas, P. 2012 Effects of vegetation on turbulence, sediment and stream morphology. ASCE J. Hydraul. Engng 138 (9), 765–776.Google Scholar
Nepf, H. M. 1999 Drag, turbulence and diffusion in flow through emergent vegetation. Water Resour. Res. 35 (2), 479–489.Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.Google Scholar
Orr, T. S., Domaradzki, J. A., Spedding, G. R. & Constantinescu, G. S. 2015 Description of the near wake of a sphere in a steady horizontal motion through a linearly stratified fluid at Re = 1000. Phys. Fluids 27, 035113.Google Scholar
Ozan, A. Y., Constantinescu, G. & Hogg, A. J. 2015 Lock-exchange gravity currents propagating in a channel containing an array of obstacles. J. Fluid Mech. 765, 544–575.Google Scholar
Plew, D. R., Cooper, G. C. & Callaghan, F. M. 2008 Turbulence-induced forces in a freshwater macrophyte canopy. Water Resour. Res. 44, W02414.Google Scholar
Righetti, M. & Armanini, A. 2002 Flow resistance in open channel flows with sparsely distributed bushes. J. Hydrol. 269, 55–64.Google Scholar
Rockwell, D. 2008 Vortex formation in shallow flows. Phys. Fluids 20, 031303.Google Scholar
Rodi, W., Constantinescu, G. & Stoesser, T. 2013 Large Eddy Simulation in Hydraulics. IAHR Monograph, p. 250. CRC Press, Taylor & Francis.Google Scholar
Rominger, J. T., Lightbody, A. F. & Nepf, H. M. 2010 Effects of added vegetation on sand bar stability and stream hydrodynamics. ASCE J. Hydraul. Engng 136 (12), 994–1002.Google Scholar
Sand-Jensen, K. & Pedersen, M. L. 2008 Streamlining of plant patches in streams. Freshwat. Biol. 53, 714–726.Google Scholar
Schultz, M., Kozerski, H.-P., Pluntke, T. & Rinke, K. 2003 The influence of macrophytes on sedimentation and nutrient retention in the lower river Spree. Water Resour. Res. 37, 569–578.Google Scholar
Sharpe, R. G. & James, C. S. 2006 Deposition of sediment from suspension in emergent vegetation. Water SA 32 (2), 211–218.Google Scholar
Simon, A., Bennett, S. J. & Neary, V. S. 2004 Riparian vegetation and fluvial geomorphology: problems and opportunities. In Riparian Vegetation and Fluvial Geomorphology (ed. Bennett, S. J. & Simon, A.), pp. 1–10. AGU.Google Scholar
Simpson, R. L. 2001 Junction flows. Annu. Rev. Fluid Mech. 33, 415–443.Google Scholar
Spalart, P. 2009 Detached eddy simulation. Annu. Rev. Fluid Mech. 41, 181–202.Google Scholar
Sukhodolov, A. & Sukhodolova, T. 2014 Shallow wake behind exposed wood-induced bar in a gravel-bed river. Environ. Fluid Mech. 14 (5), 1071–1083.CrossRefGoogle Scholar
Takemura, T. & Tanaka, N. 2007 Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 39, 694–710.Google Scholar
Tal, M. & Paola, C. 2007 Dynamic single-thread channels maintained by the interaction of flow and vegetation. Geol. Soc. Am. 35, 347–350.Google Scholar
Tanino, Y. & Nepf, H. M. 2008 Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. ASCE J. Hydraul. Engng 134 (1), 34–41.Google Scholar
Temmerman, S., Bouma, T. J., Van de Koppel, J., Van der Wal, D., de Vries, M. B. & Herman, P. M. J. 2007 Vegetation causes channel erosion in a tidal landscape. Geology 35 (7), 631–634.CrossRefGoogle Scholar
Tinoco, R. O. & Coco, G. 2016 A laboratory study on sediment resuspension within arrays of rigid cylinders. Adv. Water Resour. 92, 1–9.Google Scholar
Tinoco, R. O. & Cowen, E. A. 2013 The direct and indirect measurement of boundary stress and drag on individual and complex arrays of elements. Exp. Fluids 54 (4), 1509–1525.Google Scholar
Travin, A., Shur, M., Strelets, M. & Spalart, P. R. 2000 Detached-eddy simulations past a circular cylinder. Flow Turbul. Combust. 63, 293–313.Google Scholar
Tsujimoto, T., Kitamura, T. & Tsujikura, H.1998 Development of sand island with vegetation by repetition of flood and low-stage water. Proceedings of the 3rd International Conference on Hydro-Science and Engineering, Cottbus, Germany. University of Mississippi.Google Scholar
Vandenbruwaene, W., Temmerman, S., Bouma, T. J., Klaassen, P. C., de Vries, M. B., Callaghan, D. P., van Steeg, P., Dekker, F., van Duren, L. A., Martini, E. et al. 2011 Flow interaction with dynamic vegetation patches: implications for biogeomorphic evolution of a tidal landscape. J. Geophys. Res. 116, F01008.Google Scholar
Yang, J. Q., Chung, H. & Nepf, H. 2016 The onset of sediment transport in vegetated channels predicted by turbulent kinetic energy. Geophys. Res. Lett. 43 (11), 261–268.Google Scholar
Yuksel-Ozan, A., Constantinescu, G. & Nepf, H. 2016 Free surface gravity currents propagating in an open channel containing a porous layer at the free surface. J. Fluid Mech. 809, 601–627.Google Scholar
Zeng, J. & Constantinescu, G. 2017 Flow and coherent structures around circular cylinders in shallow water. Phys. Fluids 29 (6), 066601.Google Scholar
Zeng, J., Constantinescu, S. G. & Weber, L. 2008 A 3D non-hydrostatic model to predict flow and sediment transport in loose-bed channel bends. ASCE J. Hydraul. Res. 46 (3), 356–372.Google Scholar
Zong, L. & Nepf, H. 2011 Spatial distribution of deposition within a patch of vegetation. Water Resour. Res. 47, W03516.Google Scholar
Zong, L. & Nepf, H. 2012 Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 691, 368–391.Google Scholar