Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T18:02:49.654Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence and formation of multi-scale particle streaks in turbulent channel flows

Published online by Cambridge University Press:  26 January 2022

Yucheng Jie Open the ORCID record for Yucheng Jie [Opens in a new window] ,
Zhiwen Cui Open the ORCID record for Zhiwen Cui [Opens in a new window] ,
Chunxiao Xu Open the ORCID record for Chunxiao Xu [Opens in a new window]  and
Lihao Zhao Open the ORCID record for Lihao Zhao [Opens in a new window]
Yucheng Jie
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, 100084 Beijing, PR China
Zhiwen Cui
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, 100084 Beijing, PR China
Chunxiao Xu
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, 100084 Beijing, PR China
Lihao Zhao*
Affiliation:
AML, Department of Engineering Mechanics, Tsinghua University, 100084 Beijing, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

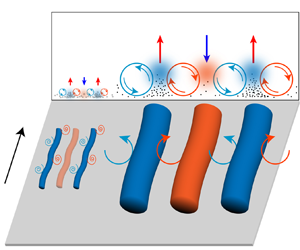
Direct numerical simulations of particle-laden turbulent channel flows at friction Reynolds number $Re_\tau$ from $600$ to $2000$ have been performed to examine the near-wall particle streaks. Different from the well-observed small-scale particle streaks in near-wall turbulence of low $Re_\tau$, the present results show large-scale particle streaks through the computational domain formed for relatively high-inertia particles at high $Re_\tau$. Transferred by large-scale sweep and ejection events ($Q^-$), these high-inertia particles preferentially accumulate in near-wall regions beneath the large-scale low-speed flow streaks observed in the logarithmic region. The corresponding Stokes numbers are associated with the lifetime of large-scale $Q^-$ structures, which increases as the Reynolds number grows. The small-scale particle streaks with a typical Stokes number $St_\nu \approx 30$ are mainly driven by the $Q^-$ structures in the buffer layer, whose lifetime is approximately $30$ in viscous time unit. Therefore, we propose a new structure-based Stokes number normalized by the lifetime of $Q^-$ structures of different scales. The relevant flow scales that control the formation of the large-scale particle streaks are parameterized by the structure-based Stokes number. The small-scale (large-scale) particle streaks are most prominent when the buffer-layer (large-scale) structure-based Stokes number approaches unity. The present findings reveal that formation of near-wall particle streaks is governed by the $Q^-$ structures of different scales, and the particles with different inertia respond efficiently to the $Q^-$ structures of corresponding scales with respect to the particle translational motion.

JFM classification

Complex Fluids: Suspensions Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 935 , 25 March 2022 , A18
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baker, L., Frankel, A., Mani, A. & Coletti, F. 2017 Coherent clusters of inertial particles in homogeneous turbulence. J. Fluid Mech. 833, 364–398.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J.K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133.CrossRefGoogle Scholar
Balakumar, B.J. & Adrian, R.J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Berk, T. & Coletti, F. 2020 Transport of inertial particles in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 903, A18.CrossRefGoogle Scholar
Bernardini, M. 2014 Reynolds number scaling of inertial particle statistics in turbulent channel flows. J. Fluid Mech. 758, R1.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2013 The effect of large-scale turbulent structures on particle dispersion in wall-bounded flows. Intl J. Multiphase Flow 51, 55–64.CrossRefGoogle Scholar
Bragg, A.D., Richter, D.H. & Wang, G. 2021 When is settling important for particle concentrations in wall-bounded turbulent flows? arXiv:2101.04607v2.Google Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32, 565–568.2.0.CO;2>CrossRefGoogle Scholar
Costa, P., Brandt, L. & Picano, F. 2020 Interface-resolved simulations of small inertial particles in turbulent channel flow. J. Fluid Mech. 883, A54.CrossRefGoogle Scholar
Eaton, J.K. & Fessler, J.R. 1994 Preferential concentration of particles by turbulence. Intl J. Multiphase Flow 20, 169–209.CrossRefGoogle Scholar
Fessler, J.R., Kulick, J.D. & Eaton, J.K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6, 3742–3749.CrossRefGoogle Scholar
Fong, K.O., Amili, O. & Coletti, F. 2019 Velocity and spatial distribution of inertial particles in a turbulent channel flow. J. Fluid Mech. 872, 367–406.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Jie, Y., Andersson, H.I. & Zhao, L. 2021 Effects of the quiescent core in turbulent channel flow on transport and clustering of inertial particles. Intl J. Multiphase Flow 140, 103627.CrossRefGoogle Scholar
Kim, K.C. & Adrian, R.J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Kline, S.J., Reynolds, W.C., Schraub, F.A. & Runstadler, P.W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
Lee, M. & Moser, R.D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_\tau \approx 5200$. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.CrossRefGoogle Scholar
Marchioli, C., Soldati, A., Kuerten, J.G.M., Arcen, B., Tanière, A., Goldensoph, G., Squires, K.D., Cargnelutti, M.F. & Portela, L.M. 2008 Statistics of particle dispersion in direct numerical simulations of wall-bounded turbulence: results of an international collaborative benchmark test. Intl J. Multiphase Flow 34, 879–893.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
McLaughlin, J.B. 1989 Aerosol particle deposition in numerically simulated channel flow. Phys. Fluids A 1, 1211–1224.CrossRefGoogle Scholar
Milici, B., Marchis, M.D., Sardina, G. & Napoli, E. 2014 Effects of roughness on particle dynamics in turbulent channel flows: a DNS analysis. J. Fluid Mech. 739, 465–478.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.CrossRefGoogle Scholar
Monty, J.P., Hutchins, N., Ng, H.C.H., Marusic, I. & Chong, M.S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Oujia, T., Matsuda, K. & Schneider, K. 2020 Divergence and convergence of inertial particles in high-Reynolds-number turbulence. J. Fluid Mech. 905, A14.CrossRefGoogle Scholar
Picano, F., Sardina, G. & Casciola, C.M. 2009 Spatial development of particle-laden turbulent pipe flow. Phys. Fluids 21, 093305.CrossRefGoogle Scholar
Reeks, M.W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 14 (6), 729–739.CrossRefGoogle Scholar
Rouson, D.W.I. & Eaton, J.K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428, 149–169.CrossRefGoogle Scholar
Sardina, G., Picano, F., Schlatter, P., Brandt, L. & Casciola, C.M. 2011 Large scale accumulation patterns of inertial particles in wall-bounded turbulent flow. Flow Turbul. Combust. 86, 519–532.CrossRefGoogle Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C.M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.CrossRefGoogle Scholar
Scherer, M., Uhlmann, M., Kidanemariam, A.G. & Krayer, M. 2022 On the role of turbulent large-scale streaks in generating sediment ridges. J. Fluid Mech. 930, A11.CrossRefGoogle Scholar
Schiller, L. & Naumann, A.Z. 1933 Ueber die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Z. Verein. Deutsch. Ing. 77, 318–320.Google Scholar
Smits, A.J., McKeon, B.J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.CrossRefGoogle Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35 (9), 827–839.CrossRefGoogle Scholar
Wang, G., Gu, H. & Zheng, X. 2020 Large scale structures of turbulent flows in the atmospheric surface layer with and without sand. Phys. Fluids 32, 106604.CrossRefGoogle Scholar
Wang, G. & Richter, D. 2020 Multiscale interaction of inertial particles with turbulent motions in open channel flow. Phys. Rev. Fluids 5, 044307.CrossRefGoogle Scholar
Wang, G. & Richter, D.H. 2019 Two mechanisms of modulation of very-large-scale motions by inertial particles in open channel flow. J. Fluid Mech. 868, 538–559.CrossRefGoogle Scholar