2.1. The FIK relation as a second moment of momentum equation

The most salient feature of the original FIK relation (Fukagata et al. Reference Fukagata, Iwamoto and Kasagi2002) is that the friction coefficient of steady, fully developed internal flows is cleanly split into a laminar friction coefficient plus the turbulent stress contribution. However, this is accomplished using a triple-integration procedure which does not immediately lend itself to intuitive interpretation (Renard & Deck Reference Renard and Deck2016). To set the stage for an angular momentum approach to external flows, a reinterpretation of the original FIK relation is presented in terms of an integral conservation law for the second moment of momentum.

The original FIK derivation is as follows. In the context of channel flow with half-height $h$, (2.2) for the mean streamwise momentum equation simplifies to

(2.3)\begin{equation} {-}\frac{1}{\rho}\frac{\partial\bar{p}}{\partial x} ={-} \nu\frac{\partial^{2} \bar{u}}{\partial y^{2}} + \frac{\partial \overline{u'v'}}{\partial y} + I^{*}_x, \end{equation}

where the streamwise inhomogeneous and transient terms are grouped together as

(2.4) \begin{equation} I^{*}_x \equiv \frac{\partial\bar{u}}{\partial t} + \frac{\partial \overline{u}^{2}}{\partial x}+\frac{\partial \bar{u}\bar{v}}{\partial y} +\frac{\partial \overline{u'^{2}}}{\partial x}-\nu\frac{\partial^{2} \bar{u}}{\partial x^{2}}. \end{equation}

Equation (2.3) is successively integrated three times, with the third integration carried across the channel. Thus, the viscous term is transformed from a second derivative of mean velocity into an integral of mean velocity across the channel, i.e. the bulk velocity

(2.5)\begin{equation} U_b = \frac{1}{h} \int_{0}^{h} \bar{u}(y) \,{{\rm d} y}. \end{equation}

The particular choice of three integrations is effective in the outcome of FIK because the bulk velocity (or flow rate) is crucial to engineering analysis of internal flows as reflected by the definition of the (Fanning) friction factor,

(2.6)\begin{equation} f_F \equiv \frac{\tau_w}{\frac{1}{2}\rho U_b^{2}}. \end{equation}

The result of triple integration, made dimensionless, is

(2.7)\begin{equation} \frac{f_F}{6} = \frac{1}{Re_b} + \int_0^{1}\left(1-\frac{y}{h}\right)\frac{-\overline{u'v'}}{U_b^{2}}d\left(\frac{y}{h}\right) - \frac{\mathcal{I}^{*}_x}{h^{2}U_b^{2}}, \end{equation}

where $Re_b \equiv U_b h / \nu$. The first term on the right-hand side is the laminar friction factor, the second is the friction enhancement due to turbulent stresses which is weighted by distance away from the wall, and $\mathcal {I}^{*}_x$ is the triple integral of the streamwise inhomogeneous and transient terms.

A vital feature of this result is that the first term is not altered when the flow becomes turbulent, but rather continues to represent the friction factor of an equivalent laminar channel flow at the same bulk Reynolds number. This property of the FIK relation allows the second term to be clearly interpreted as the added friction due to turbulence. In a way, the FIK relation may be viewed as a comparison of a laminar and turbulent channel flow, each having the same $Re_b$. The weight, $1-y/h$, quantifies how turbulent fluctuations at various distances contribute to the difference in the friction factor when $Re_b$ is held constant.

As pointed out by Bannier et al. (Reference Bannier, Garnier and Sagaut2015), an alternative derivation may be seen from Cauchy's formula for repeated integration,

(2.8)\begin{equation} \int_a^{b} {\rm d}\kern0.06em x_n \int_a^{x_n} {\rm d}\kern0.06em x_{n-1} \dots\int_a^{x_3} \int_a^{x_2} {\rm d}\kern0.06em x_1\, f(x_1) = \frac{1}{(n-1)!}\int_a^{b} {{\rm d}\kern0.06em x} (b-x)^{n-1}\, f(x). \end{equation}

Consequently, the integral conservation law for the second moment of momentum about $y=h$,

(2.9)\begin{equation} \frac{1}{2}\int_0^{h}\left(y-h\right)^{2}\left\{-\frac{1}{\rho}\frac{\partial\bar{p}}{\partial x} ={-} \nu\frac{\partial^{2} \bar{u}}{\partial y^{2}} + \frac{\partial \overline{u'v'}}{\partial y} + I^{*}_x\right\} {{\rm d} y}, \end{equation}

leads to the same result as (2.7). Therefore, the FIK relation may be equivalently derived from the integral equation for the second moment of momentum about $y=h$. In this view, the Reynolds stress redistributes streamwise momentum with respect to the wall-normal coordinate, altering the second moment of momentum balance leading to larger wall shear stress. This alternate derivation of FIK thus provides more intuition with regard to its physical meaning, as may become clearer later.

In principle, an integral conservation equation may be constructed for any order moment of momentum (Bannier et al. Reference Bannier, Garnier and Sagaut2015). For example, the zeroth-order moment of (2.3) yields the standard integral momentum relation for channel flows,

(2.10)\begin{equation} {-}\frac{{\rm d}\bar{p}}{{\rm d}\kern0.06em x} = \frac{\tau_w}{h}, \end{equation}

which has already been used in the derivation of (2.7). The particular choice of the second moment, as with the choice of triple integration, is motivated by the fact that the integral of the second moment of the viscous force,

(2.11)\begin{equation} \frac{1}{2} \int_{0}^{h} (y-h)^{2} \nu \frac{\partial^{2} \bar{u}}{\partial y^{2}} {{\rm d} y} = \nu U_b h - \frac{h^{2} \tau_w}{2 \rho} = U_b^{2} h^{2} \left( \frac{1}{Re_b} - \frac{f_F}{4} \right), \end{equation}

relates the bulk velocity (flow rate) to the wall shear stress, the two quantities used in defining the friction factor for internal flows, (2.6). This is the essential ingredient in isolating the laminar friction factor based on the bulk Reynolds number in the FIK relation. As such, the FIK relation represents a comparison of the friction factor in a turbulent channel flow to that in a laminar one at the same $Re_b$ (i.e. at the same flow rate), the difference being quantifiable by the integral of the Reynolds stress weighted by $1 - y/h$. A similar procedure may be applied to pipe flow using cylindrical coordinates (Fukagata et al. Reference Fukagata, Iwamoto and Kasagi2002).

To illustrate an important point, consider the first moment-of-momentum integral equation for a stationary, fully developed turbulent channel flow ($I_x = 0$),

(2.12)\begin{equation} \int_0^{h}\left(y-h\right)\left\{-\frac{1}{\rho}\frac{\partial\bar{p}}{\partial x} ={-} \nu\frac{\partial^{2} \bar{u}}{\partial y^{2}} + \frac{\partial \overline{u'v'}}{\partial y} \right\} {{\rm d}y}, \end{equation}

which leads to the following dimensionless relation:

(2.13)\begin{equation} \frac{f_c}{4} = \frac{1}{Re_c} + \int_{0}^{1} \frac{-\overline{ u^{\prime} v^{\prime}}}{U_c^{2}} d\left(\frac{y}{h}\right), \end{equation}

where $Re_c = U_c h / \nu$ and $f_c = \tau _w / (\tfrac {1}{2} \rho U_c^{2})$, with $U_c$ as the mean centreline velocity. In contrast to the FIK relation, (2.7), the laminar friction factor appears in (2.13) as a function of the centreline Reynolds number because the first moment of the viscous force is related to the centreline velocity rather than the flow rate,

(2.14)\begin{equation} \int_{0}^{h} (y-h) \nu \frac{\partial^{2} \bar{u}}{\partial y^{2}} {{\rm d} y} = \frac{h \tau_w}{\rho} - \nu U_c = U_c^{2} h \left( \frac{f_c}{2} - \frac{1}{Re_c} \right), \end{equation}

cf. (2.11). So the (unweighted) integral of the Reynolds stress in (2.13) quantifies the comparative difference between the friction factor of turbulent and laminar channel flows having the same $Re_c$. Thus, it is clear that the order of the moment used (equivalently, the number of successive integrations) determines the velocity scale that appears in the Reynolds number and friction factor definitions in the resulting dimensionless equations (i.e. the Reynolds number held fixed for the sake of comparison). The length scale in the Reynolds number is determined by the use of $h$ as the origin about which the moment is taken. Ultimately, the original FIK relation (second moment of momentum), (2.7), is preferred to the first moment of momentum, (2.13), in the context of internal flows, namely, determining the pressure drop associated with a given flow rate ($U_b$).

Fukagata et al. (Reference Fukagata, Iwamoto and Kasagi2002) also applied their triple-integration procedure to ZPG boundary layers, with the result,

(2.15)\begin{equation} C_f = \frac{4(1-\delta^{*}/\delta)}{Re_\delta}+4\int_0^{1}\frac{-\overline{u'v'}}{U_\infty^{2}}\left(1-\frac{y}{\delta}\right)d\left(\frac{y}{\delta}\right) - 2\int_0^{1}\left(1-\frac{y}{\delta}\right)^{2}\frac{I^{*}_x\delta}{U_\infty^{2}}d\left(\frac{y}{\delta}\right), \end{equation}

where $\delta$ is the $99\,\%$ boundary layer thickness, $\delta ^{*}$ is the displacement thickness, and the Reynolds number is $Re_\delta = U_\infty \delta / \nu$. The boundary layer skin friction coefficient $C_f$ is defined with respect to the free stream velocity:

(2.16)\begin{equation} C_f \equiv \frac{\tau_w}{\frac{1}{2}\rho U_\infty^{2}}. \end{equation}

An important difference between (2.15) for boundary layers and (2.7) for channel flows is that the first term on the right-hand side in (2.15) does not represent the friction coefficient of an undisturbed laminar boundary layer. Instead, it implicitly depends on the effects of turbulence which alter the ratio $\delta ^{*}/\delta$ by distorting the mean field due to the turbulent mixing of momentum. Thus, an important shortcoming of the original FIK relation is the failure to cleanly isolate the laminar boundary layer friction coefficient as done for the friction factor of internal flows.

Importantly, note that the definition of the skin friction coefficient for boundary layers, (2.16), is based on the free stream velocity rather than the flow rate. This difference inherently reflects the engineering context of these two flows. Internal flows are characterized by the pressure head required to produce a certain flow rate, but boundary layer drag is typically analysed relative to the velocity outside the boundary layer. It is important that the relevant engineering context informs the analysis of skin friction enhancement by turbulence. In fact, the essence of this discussion has already been pointed out by Xia et al. (Reference Xia, Huang, Xu and Cui2015), who developed a skin friction relation using a double-integration procedure based on this observation. Mathematically, the free stream velocity is analogous to the centreline velocity in the channel flow. For reasons apparent from the above discussion, an integral equation for the first moment of momentum is now developed for boundary layers rather than FIK (second moment of momentum).

2.2. A first-order moment of momentum equation for boundary layers

The starting point for constructing an integral conservation law for the first moment of momentum is the zeroth-order moment, i.e. the von Kármán integral momentum equation (von Kármán Reference von Kármán1921). This is the fundamental momentum balance relation for boundary layers, analogous to (2.10) for channel flows. This proceeds by subtracting the free stream momentum equation,

(2.17)\begin{equation} \frac{\partial U_\infty}{\partial t}+U_\infty\frac{\partial U_\infty}{\partial x} ={-}\frac{1}{\rho}\frac{\partial P_\infty}{\partial x}, \end{equation}

from (2.2) to form the streamwise momentum deficit equation,

(2.18)\begin{equation} \frac{\partial (U_\infty-\bar{u})\bar{u}}{\partial x}+\frac{\partial(U_\infty - \bar{u})\bar{v}}{\partial y}+(U_\infty-\bar{u})\frac{\partial U_\infty}{\partial x} ={-}\nu\frac{\partial^{2} \bar{u}}{\partial y^{2}} +\frac{\partial \overline{u'v'}}{\partial y} - I_x, \end{equation}

where

(2.19)\begin{equation} I_x \equiv \frac{\partial (U_\infty-\bar{u})}{\partial t}+\frac{1}{\rho}\frac{\partial (P_\infty-\bar{p})}{\partial x}+\nu\frac{\partial^{2} \bar{u}}{\partial x^{2}}-\frac{\partial \overline{u'^{2}}}{\partial x}, \end{equation}

contains all the terms typically negligible in standard high-Reynolds-number boundary layer theory. Integrating (2.18) in the wall-normal direction from zero to $\infty$ while neglecting $I_x$ leads to the von Kármán momentum integral equation,

(2.20)\begin{equation} \frac{\tau_w}{\rho} = U_\infty^{2} \frac{{\rm d}\theta}{{\rm d}\kern0.06em x}+(\delta^{*} + 2 \theta) U_\infty \frac{{\rm d} U_\infty}{{\rm d}\kern0.06em x}, \end{equation}

where

(2.21a,b)\begin{equation} \delta^{*} \equiv \int_0^{\infty}\left(1-\frac{\bar{u}(y)}{U_\infty}\right) {{\rm d} y}\quad \mathrm{and} \quad \theta \equiv \int_0^{\infty}\left(1-\frac{\bar{u}(y)}{U_\infty}\right)\frac{\bar{u}(y)}{U_\infty} {{\rm d} y} \end{equation}

are the displacement thickness and momentum thickness, respectively.

An important detail for an equation involving a moment of momentum in the boundary layer is what origin to take for this moment. Taking the moment about the wall ($y=0$) unfortunately removes the wall shear stress from the resulting relation. In the channel flow, the moment is taken about the centre of the channel, i.e. multiplication by $(y - h)^{2}$. No such geometrically imposed origin exists for the boundary layer. Instead, various boundary layer thicknesses could be used: $\delta$, $\delta ^{*}$, $\theta$, etc. This is an important distinction for boundary layers compared with internal flows. As a result, a to-be-determined length scale $\ell = \ell (x)$ must be introduced.

The moment-of-momentum integral equation is constructed by multiplying (2.18) by $y - \ell$ and integrating from $0$ to $\infty$. Dividing the result by $U_\infty ^{2} \ell$ leads to the following dimensionless relationship:

(2.22)\begin{equation} \frac{C_f}{2} = \frac{1}{Re_\ell} +\int_0^{\infty}\frac{-\overline{u'v'}}{U_\infty^{2} \ell}{{\rm d} y} +\frac{\partial \theta_\ell}{\partial x} -\frac{\theta-\theta_\ell}{\ell}\frac{{\rm d} \ell}{{\rm d}\kern0.06em x} +\frac{\theta_v}{\ell} +\frac{\delta_\ell^{*} +2\theta_\ell}{U_\infty}\frac{\partial U_\infty}{\partial x} +\mathcal{I}_{x,\ell}, \end{equation}

where $Re_\ell = U_\infty \ell / \nu$, and

(2.23)\begin{equation} \mathcal{I}_{x,\ell} \equiv \int_0^{\infty}\left(1-\frac{y}{\ell}\right)\frac{I_x}{U_\infty^{2}}{{\rm d} y} \end{equation}

is the term which contains everything negligible under boundary layer theory assumptions. The length scales introduced in (2.22) are generalizations of the displacement and momentum thicknesses,

(2.24)$$\begin{gather} \delta_\ell^{*} \equiv \int_0^{\infty}\left(1-\frac{y}{\ell}\right)\left(1-\frac{\bar{u}(y)}{U_\infty}\right) {{\rm d} y}, \end{gather}$$

(2.25)$$\begin{gather}\theta_\ell \equiv \int_0^{\infty}\left(1-\frac{y}{\ell}\right)\left(1-\frac{\bar{u}(y)}{U_\infty}\right)\frac{\bar{u}(y)}{U_\infty} {{\rm d} y} \end{gather}$$

and

(2.26)\begin{equation} \theta_v \equiv \int_0^{\infty}\left(1-\frac{\bar{u}(y)}{U_\infty}\right)\frac{\bar{v}(y)}{U_\infty} {{\rm d} y}. \end{equation}

Equation (2.22) encapsulates the main theoretical result of this paper. Note that (2.22) has been derived assuming a no-penetration condition at the wall, but it is straightforward to relax this assumption and include the effect of blowing and suction. Xia et al. (Reference Xia, Huang, Xu and Cui2015) introduced the idea of using a double-integration procedure for boundary layers, arriving at a relation that shares some similarities with (2.22) derived here. In fact, the first two terms on the right-hand side of (2.22) are precisely equal to those of Xia et al. (Reference Xia, Huang, Xu and Cui2015) with the choice of $\ell = \delta /2$ (half of the disturbance thickness), as well as truncating the integral at $y = \delta$. The key difference between (2.22) and the skin friction relation of Xia et al. (Reference Xia, Huang, Xu and Cui2015) is the introduction of the length scale $\ell$ in the former. This flexibility to choose $\ell$ crucially facilitates the interpretation of the AMI equation, as will be explained shortly. The length scale, $\ell$, can also be introduced using a modified double-integration procedure, as shown by Johnson (Reference Johnson2019). The resulting equation is equivalent to that of a single integration of the first moment of momentum, (2.22). Xia, Zhang & Yang (Reference Xia, Zhang and Yang2021) considered a similar double-integration procedure for predicting the wall shear stress from outer flow measurements. Double integral (or first moment) relations have also recently been introduced for high-speed boundary layers (Xu, Wang & Chen Reference Xu, Wang and Chen2021; Wenzel, Gibis & Kloker Reference Wenzel, Gibis and Kloker2022).

2.3. Interpretation as an integral conservation law for angular momentum

One important limitation of the original FIK relation is the difficulty of interpreting the meaning of triple integration, and hence understanding the $1 -y/h$ weighting of the Reynolds stress integral (Renard & Deck Reference Renard and Deck2016). In this subsection, each term of (2.22) is discussed and interpreted in an angular momentum framework. Though not pursued here, a similar reinterpretation of the original FIK could be done in terms of the second-order moment of momentum.

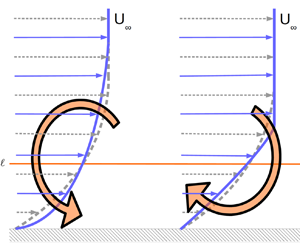
The concept of moment of momentum can be thought of as the angular momentum of a flow, with streamwise coordinate $x$ being a time-like variable. The origin about which the moment is taken, $\ell = \ell (x)$, is allowed to change as the analysis marches downstream. This provides an intuitive interpretation of (2.22) as an integral conservation equation for the angular momentum of a boundary layer mean velocity profile, where torques redistribute momentum in the wall-normal direction, see figure 1. The wall shear stress itself acts as a torque which must be balanced by the opposing torques and the streamwise growth of the boundary layer's angular momentum.

Figure 1. For a fixed $U_\infty$, a torque that (a) redistributes momentum towards the wall will act to increase the skin friction, or (b) redistributes momentum away from the wall will act to decrease the skin friction.

2.3.1. Viscous force and laminar friction coefficient

The friction coefficient on the left-hand side and the first term on the right-hand side of (2.22) originate from the first-order moment of the viscous force,

(2.27)\begin{equation} T_{\nu,\ell} = \int_0^{\infty}\nu(y-\ell)\frac{\partial^{2} \bar{u}}{\partial y^{2}} {{\rm d} y} = \frac{\ell \tau_w}{\rho}-\nu U_\infty = U_\infty^{2} \ell \left(\frac{C_f}{2} - \frac{1}{Re_\ell}\right), \end{equation}

which is like the viscous ‘torque’ about $y = \ell (x)$. The middle expression of (2.27) confirms that the first moment integral transforms the viscous term in (2.18) into the wall shear stress and the free stream velocity, precisely the two quantities used for forming the friction coefficient, as discussed in § 2.2. It is evident from the right-hand side of (2.27) that choosing $\ell$ such that

(2.28)\begin{equation} \frac{C_f}{2} = \frac{1}{Re_\ell} \end{equation}

selects $\ell$ to be the centre of action of the viscous force (the viscous torque about $\ell$ is zero). When (2.28) is satisfied for a ZPG laminar boundary layer,

(2.29)\begin{equation} \frac{C_f}{2} = \frac{1}{Re_\ell} = \frac{0.332}{\sqrt{Re_x}} = \frac{0.221}{Re_\theta} = \frac{0.571}{Re_{\delta^{*}}} = \frac{1.63}{Re_{\delta}}. \end{equation}

Such a choice is precisely what isolates the laminar friction factor in (2.22). That is, the other terms in (2.22) vanish for the ZPG laminar boundary layer when

(2.30)\begin{equation} \ell = 3.01\sqrt{\frac{\nu x}{U_\infty}} = 4.54\theta = 1.75\delta^{*} = 0.613\delta. \end{equation}

For boundary layers with turbulence or non-ZPGs, (2.30) represents four distinct choices for $\ell (x)$. The friction coefficient of the equivalent ZPG laminar boundary layer, $Re_{\ell }^{-1}$, depends on the choice of length scale to which $\ell (x)$ will be proportional.

There is a basic physical reason why such a choice must be made when isolating the ZPG laminar friction coefficient. The physical meaning of the ‘laminar contribution’ to the skin friction in (2.22) is that a turbulent boundary layer (or laminar boundary layer with non-zero free stream pressure gradient) is being compared with an equivalent ZPG laminar, i.e. Blasius boundary layer (Blasius Reference Blasius1907). However, there is no unique choice for such a comparison to be made. One may choose to compare a turbulent boundary layer with a laminar one at the same $Re_x$, equivalent to the choice of $\ell \sim \sqrt {\nu x / U_\infty }$. Alternatively, the choice may be made to compare a turbulent boundary layer with a laminar boundary layer having the same $Re_\theta$, i.e. $\ell \sim \theta$. Other choices have analogous interpretations. There is not one unique laminar boundary layer with which a turbulent boundary layer can be compared. One must choose what length scale to use in the definition of Reynolds number fixed for the sake of comparison. The velocity scale that appears in the Reynolds number is set by the choice of the first moment of momentum. Using the second moment of momentum, as done in FIK, results in a velocity scale related to the mass flow rate deficit, $U_{\dot {m}} \approx U_\infty ( 1 - {\delta ^{*}}/{\delta })$, see (2.15).

Of course, the same choice is theoretically available in the case of the second moment of momentum integral equations for the channel flow, (2.7). Instead of choosing the channel half-height as the origin for the moments, for example, one may choose a length scale defined similarly to the momentum thickness, $\theta$. The laminar friction factor in that case would be written in terms of $Re_\theta$ and the implicit comparison between a laminar and turbulent channel flow will be performed keeping $Re_\theta$ the same between the two flows. As it stands, it is natural to use the channel half-height for such a comparison, because $h$ is both the geometrically imposed length scale and the length scale indicative of the width of the viscous flow layer. In the boundary layer, by contrast, the geometric length scale is $x$, while the width of the viscous layer is quantified as $\theta$, $\delta ^{*}$ or $\delta$. Therefore, using the integral conservation law for angular momentum in boundary layers with different choices of $\ell$ can lead to different insights.

Note that the skin friction relation of Xia et al. (Reference Xia, Huang, Xu and Cui2015) can be reproduced from (2.22) with the choice $\ell = \delta /2$ (and somewhat arbitrarily truncating the integral at $y = \delta$). This choice of $\ell$ differs by a coefficient from the rightmost expression in (2.29) and (2.30). Indeed, (2.22) with $\ell = 0.613\delta$ and the relation from Xia et al. (Reference Xia, Huang, Xu and Cui2015) would yield qualitatively similar results for the first two terms when applied to the same dataset (for both terms, the latter would be roughly $20\,\%$ larger than the former). With the change in coefficient from $0.613$ to $0.5$, however, the laminar skin friction coefficient is no longer properly isolated in the first term. Thus, the fundamental interpretation of the first term as a laminar skin friction entirely breaks down, and the essential property that the FIK relation enjoys for the channel flow (i.e. the isolation of the laminar friction) cannot be recovered using the approach of Xia et al. (Reference Xia, Huang, Xu and Cui2015). As a result, the other terms cannot be interpreted as augmentations relative to the laminar case. A similar comment applies to the compressible flow relations of Xu et al. (Reference Xu, Wang and Chen2021) and Wenzel et al. (Reference Wenzel, Gibis and Kloker2022).

2.3.2. Reynolds stress and turbulent contribution

The second term on the right-hand side of (2.22) represents the torque of the Reynolds shear stress, $-\overline {u^{\prime } v^{\prime }}$, henceforth called simply the Reynolds stress because other components of the Reynolds stress tensor do not play a significant role for the dynamics discussed in this paper. The Reynolds stress derivative in (2.18) integrates to zero across the boundary layer when not weighted by $y - \ell$, and thus does not contribute to the von Kármán momentum integral equation. However, the first moment of this term is

(2.31)\begin{equation} T_{t,\ell} = \int_{0}^{\infty} (y-\ell) \frac{\partial \overline{ u^{\prime} v^{\prime}}}{\partial y} {{\rm d} y} ={-} \int_{0}^{\infty} \overline{u^{\prime} v^{\prime}} \,{{\rm d} y} \end{equation}

which has no explicit dependence on $\ell$. The Reynolds torque quantifies the direct contribution of turbulence to increasing the boundary layers' friction coefficient by redistributing momentum towards the wall.

In contrast to the channel flow, the integral of the Reynolds stress is unweighted. This fact emphasizes that the relative influence of turbulent fluxes on skin friction depends on the engineering context of the flow under consideration. That is, boundary layers are characterized by a free stream velocity and thus the turbulent enhancement of skin friction above that of an equivalent laminar flow proceeds from the first moment of momentum and leads to an unweighted integral of the Reynolds stress. In contrast, channel and pipe flows are characterized primarily by a mass flow rate (bulk velocity), so the turbulent enhancement of friction factor above that of an equivalent laminar flow uses the second moment of momentum to get a linearly weighted integral of the Reynolds stress.

2.3.3. Streamwise growth of the angular momentum

The first moment of the streamwise flux of momentum deficit is

(2.32)\begin{equation} \int_{0}^{\infty} (y-\ell) \frac{\partial \left[ \left(U_\infty - \bar{u}\right) \bar{u} \right]}{\partial x} {{\rm d} y} ={-} U_\infty^{2} \ell \left[ \frac{{\rm d}\theta_\ell}{{\rm d}\kern0.06em x} - \frac{\theta - \theta_\ell}{\ell} \frac{{\rm d}\ell}{{\rm d}\kern0.06em x} + \frac{2 \theta_\ell}{U_\infty} \frac{{\rm d}U_\infty}{{\rm d}\kern0.06em x} \right]. \end{equation}

Recall that $\theta$ is the momentum thickness, the flux deficit of streamwise momentum. Similarly, $\theta _\ell$ is the flux deficit of streamwise angular momentum about $\ell$ defined in (2.25). Note that $\theta - \theta _\ell$ is the angular momentum thickness about $y = 0$. The first two terms on the right-hand side of (2.32) represent the rate of streamwise growth of the angular momentum thickness relative to the growth rate of $\ell (x)$. Together, they capture the indirect impact of turbulence and free stream pressure gradients on wall shear stress via changes to the rate of boundary layer growth relative to the baseline laminar case. The last term on the right-hand side is due to the direct effect of pressure gradients, so will be discussed in § 2.3.5.

2.3.4. Mean wall-normal flow

The first moment of the wall-normal momentum flux is

(2.33)\begin{equation} \int_{0}^{\infty} (y-\ell) \frac{\partial \left[ \left(U_\infty - \bar{u}\right) \bar{v} \right]}{\partial y} {{\rm d} y} ={-} U_\infty^{2} \theta_v, \end{equation}

where $\theta _v$ is a generalization of the momentum thickness to the wall-normal flux, defined in (2.26). This term represents the redistribution of angular momentum via mean flow away from the wall. In turbulent boundary layers, the mean wall-normal flux is usually smaller than the flux generated by the Reynolds stress, but both enhance the flux of momentum across the boundary layer so as to increase the required wall shear stress in the AMI equation (provided that the mean velocity is away from the wall).

2.3.5. Non-zero free stream pressure gradients

The moment of the free stream acceleration term in (2.18) is

(2.34)\begin{equation} \int_{0}^{\infty} (y-\ell) (U_\infty - \bar{u}) \frac{{\rm d}U_\infty}{{\rm d}\kern0.06em x} {{\rm d} y} ={-} \ell U_\infty \frac{{\rm d}U_\infty}{{\rm d}\kern0.06em x} \delta_{\ell}^{*}, \end{equation}

where $\delta _\ell ^{*}$ is the displacement thickness of the angular momentum about $y = \ell$. The negative sign moves it from the left-hand side of (2.18) to the right-hand side of (2.22). Taken together with the final term of (2.32), the pressure gradient torque is

(2.35)\begin{equation} T_{\boldsymbol{\nabla} p, \ell} = \ell U_\infty \frac{{\rm d}U_\infty}{{\rm d}\kern0.06em x} (\delta_\ell^{*} + 2 \theta_\ell). \end{equation}

This represents the direct influence of the free stream pressure gradient on the wall shear stress. A favourable pressure gradient accelerates the free stream velocity, which works to increase the wall shear stress. Conversely, an adverse pressure gradient with decelerating free stream velocity leads to lower wall shear stress.

2.3.6. Summary

Equation (2.22) is interpreted as an integral conservation principle for angular momentum about $\ell (x)$, with streamwise distance, $x$, treated as a time-like variable. Interestingly, this approach hearkens back to efforts in the 1960s, prior to the widespread use of Reynolds-averaged Navier–Stokes models, to march moment-of-momentum integral equations together with the von Kármán momentum integral equation for turbulent boundary layers (Kline et al. Reference Kline, Morkovin, Sovran and Cockrell1968).

To summarize, the terms in (2.22) can be interpreted as follows:

(2.36)$$\begin{gather} \frac{1}{Re_\ell} \longrightarrow C_f\ \mathrm{of~Blasius~boundary~layer~at~same~}Re_\ell, \end{gather}$$

(2.37)$$\begin{gather}\int_0^{\infty}\frac{-\overline{u'v'}}{U_\infty^{2} \ell}{{\rm d} y} \longrightarrow \mathrm{torque~of~turbulent~momentum~flux}, \end{gather}$$

(2.38)$$\begin{gather}\frac{\partial \theta_\ell}{\partial x}-\frac{\theta-\theta_\ell}{\ell}\frac{{\rm d} \ell}{{\rm d}\kern0.06em x} \longrightarrow \mathrm{streamwise~growth~of~angular~momentum~about}~\ell, \end{gather}$$

(2.39)$$\begin{gather}\frac{\theta_v}{\ell} \longrightarrow \text{torque due to the mean wall-normal flux}, \end{gather}$$

(2.40)$$\begin{gather}\frac{\delta_\ell^{*}+2\theta_\ell}{U_\infty}\frac{\partial U_\infty}{\partial x} \longrightarrow \mathrm{torque~of~free stream~pressure~gradient} \end{gather}$$

and

(2.41)\begin{equation} \mathcal{I}_{x,\ell} \longrightarrow \mathrm{departure~from~boundary~layer~approximations}. \end{equation}

Importantly, the friction coefficient of the Blasius boundary layer is isolated in the first term. This laminar term is only a function of $Re_\ell$, so it is insensitive to changes in the shape of the mean velocity profile. As such, it does not change as the flow transitions to turbulence or experiences free stream pressure gradients. This fact enables the simple interpretation of the AMI equation, (2.22), as a comparison of a boundary layer with the equivalent Blasius boundary layer having the same $Re_\ell$. As discussed above, the FIK relation for boundary layers, (2.15), does not have this property. Furthermore, unlike the original FIK (a second moment equation) the Reynolds stress integral is unweighted. The difference in weighting may be traced to the difference in engineering context for internal and external flows.

2.4. Comparison with an integral conservation law for mean kinetic energy

Renard & Deck (Reference Renard and Deck2016) derived a relationship for skin friction based on an integral conservation law for mean kinetic energy equation in a reference frame moving with the free stream. One of the key results of this energetic approach was the weighting of the Reynolds stress integral with the mean velocity gradient. This approach also allows for an intuitive explanation of the turbulent contribution to skin friction in terms of turbulent kinetic energy production. For a ZPG boundary layer, the equation of Renard & Deck (Reference Renard and Deck2016) is

(2.42)\begin{align} \frac{C_f}{2} &= \frac{1}{U_\infty^{3}}\int_0^{\infty}\nu\left(\frac{\partial\bar{u}}{\partial y}\right)^{2} {{\rm d} y} + \frac{1}{U_\infty^{3}}\int_0^{\infty}-\overline{u'v'}\frac{\partial \bar{u}}{\partial y} {{\rm d} y} \nonumber\\ &\quad + \frac{1}{U_\infty^{3}}\int_0^{\infty}\left(\bar{u}-U_\infty\right)\left(\bar{u}\frac{\partial \bar{u}}{\partial x}+\bar{v}\frac{\partial\bar{u}}{\partial y}\right) {{\rm d} y}. \end{align}

The interpretation of skin friction contributions within an energetic framework is an attractive feature of this equation. However, the viscous term cannot be interpreted as the skin friction of an equivalent undisturbed laminar boundary layer, because it depends strongly on the shape of the mean velocity profile, which is severely distorted when the flow transitions to turbulence, regardless of whether one keeps a Reynolds number fixed. The RD relation is best interpreted not in terms of skin friction enhancement relative to an equivalent laminar boundary layer, but as an integral energy budget. That is, the RD relation quantifies how much of the mean kinetic energy introduced by a moving wall is directly dissipated by mean viscous forces or is converted to turbulent kinetic energy and dissipated through the energy cascade.

By using the AMI equation rather than energy conservation, our present approach for external flows forms a unified framework with the original FIK relation for internal flows. The most salient feature of both AMI for external flows and FIK for internal flows is the isolation of the equivalent laminar friction coefficient in a single term that depends only on the Reynolds number appropriate for their respective engineering contexts. The AMI equation introduced here is also a natural extension of classical momentum integral theory for boundary layers (von Kármán Reference von Kármán1921). Pressure gradient effects are seamlessly incorporated into the formulation, as are remaining terms that are negligible in standard boundary layer theory but may be important in boundary layers undergoing rapid change, which could be important in some applications. The integrals are formally carried out from $0$ to $\infty$, aiding interpretability by ensuring that the integrands vanish in the free stream.

There are, in theory, an uncountable number of skin friction relations which may be developed based on integral conservation laws, whether by taking any order moment of momentum or energy or another quantity altogether. The uniqueness of the AMI equation for boundary layers is the ability to isolate the skin friction of a Blasius boundary layer in a single term as a function only of $Re_\ell$ based on the free stream velocity $U_\infty$ and a user's choice of length scale $\ell$ to facilitate the desired interpretation. That is, the AMI equation uniquely establishes how flow features (such as the Reynolds stress) throughout the boundary layer flow contribute to changing the mean skin friction relative to a ZPG laminar boundary layer having the same $Re_\ell$. Further, the AMI equation lends itself to an intuitive physical interpretation in terms of torques acting on the mean velocity profile to alter its angular momentum.

In view of the above points, it is the authors’ opinion that the AMI equation introduced here should be viewed as complementary to the integral energy equation of Renard & Deck (Reference Renard and Deck2016) for analysing boundary layer physics. The integral second moment of momentum equation developed by Fukagata et al. (Reference Fukagata, Iwamoto and Kasagi2002) is more suitable for internal flows such as channels or pipes.

4.1. Simulation datasets

4.1.1. H-type natural transition

The first transition simulation is an H-type laminar-to-turbulent transition with minimal domain extent in the spanwise direction (Herbert Reference Herbert1988; Sayadi et al. Reference Sayadi, Hamman and Moin2013). The purpose of including this simulation in the analysis is to study the skin friction overshoot in a carefully cultivated natural transition scenario. The natural instability gives rise to hairpin-like coherent structures which breakdown rather abruptly at a fixed location.

This case is simulated by the authors using a similar set-up to the one presented by Lozano-Durán, Hack & Moin (Reference Lozano-Durán, Hack and Moin2018). Transition is triggered by imposing an inflow boundary condition that is the sum of the Blasius solution, a fundamental TS wave of non-dimensional frequency $2F = \omega \nu /U_\infty ^{2} = 1.2395 \times 10^{-4}$ and a subharmonic mode of frequency $F$. These modes are the solution to the local Orr–Sommerfeld–Squire problem at $Re_x = 1.8 \times 10^{5}$. The parabolized stability equations were used to march a small initial perturbation to the DNS inflow location. The DNS uses a staggered second-order central finite-difference method with a second-order Runge–Kutta scheme for time advancement combined with the fractional-step procedure (Kim & Moin Reference Kim and Moin1985). The simulation domain is spanwise periodic, similar to the work of Lozano-Durán et al. (Reference Lozano-Durán, Hack and Moin2018), but narrower in spanwise extent with a size equal to the oblique disturbance wavelength $2{\rm \pi} /\beta$ (Elnahhas et al. Reference Elnahhas, Johnson, Lozano-Durán and Moin2019). Here, $\beta$ is the oblique disturbance wavenumber associated with the subharmonic mode. Figure 4 shows a snapshot of the flow field's wall-normal velocity, illustrating the staggered arrangement of $\varLambda$-vortices associated with H-type transition. There exists only a single $\varLambda$-vortex at any streamwise location in the simulation domain. The $Re_\theta$ range of this simulation extends from approximately $415$ to $1105$ in the streamwise direction.

Figure 4. Wall-normal velocity at $y=0.02 \delta _{inlet}$ for the H-type transition.

4.2. Analysis of transitional boundary layers

At the beginning of the laminar-to-turbulent transition region, the skin friction coefficient departs from that of a Blasius profile. By the end of transition, the skin friction coefficients of the three cases approximately collapse with a turbulent boundary layer correlation (White Reference White2005). Figure 5 shows the skin friction coefficient, $C_f$, as a function of both $Re_\theta$ and $Re_x$ for the three transitional datasets. It can be seen that there is a better collapse in the skin friction coefficient when plotted versus $Re_\theta$ as opposed to $Re_x$, as also observed by Sayadi et al. (Reference Sayadi, Hamman and Moin2013). This indicates a low sensitivity of the skin friction in the fully turbulent boundary layer to the specific transition mechanism when characterized in terms of local boundary layer thickness ($\theta$), as opposed to absolute streamwise distance from the boundary layer origin ($x$). This observation motivates a focus on $\ell \sim \theta$ for analysis of the transitional boundary layer using the AMI equation, that is, compared with the Blasius solution having the same $Re_\theta$.

Figure 5. Skin friction coefficient, $C_f$, as a function of both $Re_\theta$ and $Re_x$ for the three transitional boundary layers considered: H-type simulation (, red); JHTDB BL (, green); Wu BL (, blue); laminar solution $C_f/2 = 0.332/\sqrt {Re_x} = 0.221/Re_\theta$ (- -); turbulent correlation $C_f/2 \approx 0.029/Re_x^{1/5} \approx 0.013/Re_\theta ^{1/4}$ (–).

Figure 6 shows the different contributions to the skin friction coefficient in the AMI equation for each of the three transitional datasets. The free stream pressure gradient and negligible terms, $\mathcal {I}_{x,\ell }$, are omitted due to being approximately zero. Figure 7 groups each of the contributions for all three datasets and normalizes them by the local skin friction value to identify the regions where the relative contributions are strongest. Using these two figures, several observations can be made regarding both the absolute and relative contributions of each of the terms in (2.22).

Figure 6. Terms in the AMI relation of the mean skin friction coefficient, $C_f$ during transition, as a function of $Re_\theta$ with $\ell \sim \theta$. Panel (a) corresponds to the H-type transition; (b) corresponds to the JHTDB bypass transition; (c) corresponds to the Wu bypass transition.

Figure 7. Terms in the AMI relation of the mean skin friction coefficient, $C_f$ during transition, as a function of $Re_\theta$ with $\ell \sim \theta$ normalized by the local skin friction coefficient $C_f/2$: H-type transition ($\Box$, red); JHTDB bypass transition ($\circ$, green); Wu bypass transition ($\triangle$, blue). The solid black line is the normalized local $C_f/2$ for comparison, and $(.)^{*}$ indicates the normalized quantities.

For all datasets, the direct impact of enhanced momentum flux (Reynolds stress integral) on skin friction,

(4.1)\begin{equation} \int_{0}^{\infty} \frac{-\overline{u^{\prime} v^{\prime}}}{U_\infty^{2} \ell} {{\rm d} y}, \end{equation}

is approximately negligible near the inflow when the perturbations are small, grows to a peak near the breakdown region, as observed in the H-type transition case, and then enters a slow decay in the fully turbulent region, as the skin friction itself slowly decays. The peak in the Reynolds stress integral contribution occurs at $Re_\theta \approx 475\text {--}525$, in excess of the local $C_f/2$ value for both bypass transition cases. For the H-type transition case, it peaks at $Re_\theta \approx 630$ with greater intensity due to the sharpness of transition. These values shift slightly when the relative contributions in figure 7 are considered. Regardless, the peak in the Reynolds stress integral contribution occurs during the laminar-to-turbulent transition and is upstream of the peak in the skin friction coefficient for all three datasets.

The peak in the Reynolds shear stress integral is substantially larger in the natural H-type transition than in the bypass cases. This is due to the relative degree of intermittency in either scenario, given the effect of averaging on intermittent turbulent spots in the bypass transition simulations. Using a dynamic mode decomposition of composite skin friction and vortical structure data, Sayadi et al. (Reference Sayadi, Schmid, Nichols and Moin2014) showed that a few low-order modes corresponding to the legs of the $\varLambda$-vortices are responsible for the bulk of the mean Reynolds shear stress during natural transition. In essence, around each $\varLambda$-vortex there are large local contributions to the Reynolds shear stress, and the consistent breakdown location due to the periodicity of the $\varLambda$-vortices in the H-type simulation allows these peaks to persist after spanwise and temporal averaging.

The observed peaks in the H-type transition could qualitatively be similar to what occurs locally near the onset of turbulent patches in the Wu boundary layer, as $\varLambda$-vortices were also observed at the onset of these patches (Wu et al. Reference Wu, Moin, Wallace, Skarda, Lozano-Durán and Hickey2017). However, the spatiotemporal intermittency of these patches in the bypass transition case smooths-out this behaviour when averaging is applied. Whether stark or subtle, the peak of the Reynolds stress integral is greater than the local $C_f/2$ value in all three transitional boundary layers, implying that other flow features are working against the Reynolds stress to mitigate its effect on the peak skin friction.

The normalized contribution of the streamwise growth of a laminar ZPG laminar boundary layer was shown in figure 2( f) to be around $-0.3$, indicating that streamwise growth of angular momentum thickness reduces the demand for skin friction torque at the wall. For the Blasius case, by construction, this is offset by the equal and opposite torque of the velocity away from the wall, $\theta _v$. Figure 6 shows that for the bypass transition cases, the contribution of the streamwise growth slowly decreases in magnitude in the early stages of transition before slightly increasing in magnitude as the Reynolds stress grows rapidly. It finally settles to a relative contribution of $-0.2$ after the transition to turbulence is complete, a value shared by the H-type transition case as well, as seen in figure 7. Thus, the variation of the angular momentum thickness growth rate during transition is one factor that opposes the Reynolds stress contribution to the skin friction, albeit weakly.

In the natural H-type transition, the streamwise growth term has an exaggerated form of the trends in the bypass case, due to the lack of spatiotemporal intermittency. During early transition, it not only decreases in magnitude but also changes sign, becoming a positive contributor towards the skin friction at the wall. As transition to turbulence intensifies, it plunges back negative, in opposition to the peak Reynolds stress integral. Examining the mean velocity profiles within this narrow region shows that the positive contribution of the streamwise growth of angular momentum is correlated with the existence of an internal inflection point in the mean velocity profile in the H-type simulation, which does not exist upstream or downstream of this region and is also not found in the bypass transition cases. This corroborates the finding by Hack & Moin (Reference Hack and Moin2018) of an inflection point in the streamwise velocity profile at the centre of individual $\varLambda$-vortices in the H-type transition of Sayadi et al. (Reference Sayadi, Hamman and Moin2013). It is plausible that inflection points occur locally in similar structural regions in the Wu bypass transition case prior to the inception of a turbulent spot, becoming obscured due to spanwise and temporal filtering of the spatiotemporally intermittent nature of these turbulent spots.

A boundary layer typically has a net positive wall-normal velocity due to mass conservation as the fluid in the boundary layer is decelerated. This flux carries streamwise momentum deficit away from the wall, affecting the AMI equation so as to require increased skin friction. In the Blasius case, this directly offsets the effect of streamwise growth. However, the opposite is observed during the region of transition corresponding to $265 \leqslant R_\theta \leqslant 550$ for the bypass cases, and $450 \leqslant Re_\theta \leqslant 700$ for the H-type transition. Here, an influential region of negative wall-normal velocity effectively reduces the skin friction required to balance the AMI equation. This effect is much more pronounced in the H-type transition primarily due to the lack of intermittency, causing the breakdown to turbulence to occur in a fixed spatial region. Figure 8 shows the integrand of $\theta _v$ for the H-type transition case, illustrating the negative wall-normal velocity for $450 \leqslant Re_\theta \leqslant 700$. In contrast, the negative mean wall-normal velocity in the bypass transition cases, while observed, is much more subtle due to spanwise and temporal averaging over intermittent turbulent spots.

Figure 8. Integrand of $\theta _v$, $(1-\bar {u}/U_\infty )\bar {v}/U_\infty$ showing net downward wall-normal flow around the rapid breakdown region of the flow for the H-type transition case. The wall-normal coordinate is normalized by the value of $\delta _{98}$ at the inlet which represents boundary layer thickness.

In all three simulations, the peak negative wall-normal flux occurs during the rapid growth of the Reynolds stress integral, helping to offset the impact of $-\overline {u^{\prime } v^{\prime }}$ on the skin friction. Finally, the Blasius skin friction, ${\sim }Re_\theta ^{-1}$, monotonically decreases through the transitional region, so that it is non-zero but relatively small compared with other terms in the AMI equation at the end of transition.

For each of these cases, the torque from the free stream pressure gradient is not exactly zero due to imperfect boundary conditions at the top of the finite simulation domain. It is quite small, however, as are the terms typically neglected in boundary layer theory, $\mathcal {I}_{x,\ell }$. Nonetheless, these contributions helped close the AMI equation, (2.22), within $2\,\%$ error on average for $\ell \sim \theta$. As such, departures from boundary layer theory and the nominally ZPG were small but detectable.

4.3. Fully turbulent boundary layers

Another salient feature of figure 7 is that each term in the AMI equation begins to collapse for the three different simulations as a function of $Re_\theta$ at the end of transition when normalized by the skin friction coefficient. Similar collapse had already been observed for the skin friction by Sayadi et al. (Reference Sayadi, Hamman and Moin2013) as well as in figure 5. Figure 9 shows the continuation of figure 7 into the fully turbulent regime. The three transitional datasets differ in their transition mechanism and in the streamwise extent of the simulation. Nonetheless, all three cases produce indistinguishable results for the AMI equation throughout the entirety of their fully turbulent regions. This is further evidence suggesting that the specific transition mechanism has been forgotten in the chaos of turbulence.

Figure 9. Terms in the AMI relation of the mean skin friction coefficient, $C_f$ in the fully developed turbulent region, as a function of $Re_\theta$ with $\ell \sim \theta$, normalized by the local value of $C_f/2$: H-type transition ($\Box$, red); JHTDB bypass transition ($\circ$, green); Wu bypass transition ($\triangle$, blue). The solid black line is the normalized local $C_f/2$ for comparison, and $(.)^{*}$ indicates the normalized quantities.

Aside from the collapse of the three datasets, the most striking feature of figure 9 is that the torque from the Reynolds stress integral is the dominant term. In fact, when normalized by the skin friction torque, the Reynolds stress integral is approximately unity throughout the fully turbulent regime. This means that the rest of the terms participating in the AMI equation approximately cancel, leaving the skin friction as equal to the integral of the Reynolds stresses alone. This occurs for $\ell \sim \theta$, but not other choices. This observation may be restated as

(4.2)\begin{equation} \int_{0}^{\infty} -\frac{\overline{u^{\prime} v^{\prime}}}{u_*^{2}} \frac{{\rm d} y}{\theta} = \text{const.} \approx 4.54 = \left(Re_\theta \frac{C_f}{2} \right)_{\text{Blasius}}^{{-}1}{,} \end{equation}

where $u_* = \sqrt {\tau _w/\rho }$ is the friction velocity, and the constant $4.54$ enters this expression through the skin friction of a Blasius boundary layer, (2.29) and (2.30). The approximate equality with the Blasius friction coefficient seems to be pure coincidence, seeing as that constant is determined from laminar boundary layer theory with no apparent connection to turbulent boundary layer dynamics. However, the fact that the integral of the Reynolds stress, $\int _0^{\infty } -\overline {u^{\prime } v^{\prime }} \,{{\rm d} y}$, apparently scales with $u_*^{2} \theta$ may have more significance. This behaviour is observed for all three transitional BL simulations considered, and so it appears to be independent of the type of transition scenario (natural versus bypass).

The AMI equation results for the turbulent boundary layer DNS of Sillero et al. (Reference Sillero, Jiménez and Moser2013) are shown in figure 10. This simulation used a recycling–rescaling procedure for the inlet rather than including the transitional region within the computational domain, enabling them to reach higher Reynolds numbers. Each term in the AMI equation with $\ell \sim \theta$, normalized by $C_f/2$, is qualitatively similar to the results of the transitional datasets. However, some small discrepancies are noticeable; for example, the normalized Reynolds stress integral slightly exceeds unity. Possible explanations for this observation are discussed in Appendix B, where more specific details regarding the calculations for this dataset are given. Note that to compute the AMI terms for the Sillero boundary layer, a reformulation of the streamwise growth term was necessary.

Figure 10. Terms in the AMI equation of the mean skin friction coefficient, $C_f$ in the fully turbulent recycled boundary layer of Sillero et al. (Reference Sillero, Jiménez and Moser2013), as a function of $Re_\theta$ with $\ell \sim \theta$ normalized by the local value of $C_f/2$.

One possible explanation for the scaling of the Reynolds stress integral with the friction velocity and momentum thickness is self-similarity of the Reynolds stress profile, $\overline {u^{\prime } v^{\prime }} = u_*^{2} f(y/\theta )$. However, figure 11 shows that this is only approximately true. Reynolds stress profiles from the fully turbulent region of the Wu transitional boundary layer dataset are plotted against $y / \ell$ with $\ell = 4.54 \theta$. As expected, the near-wall peak in Reynolds stress grows and approaches the wall as $Re_\theta$ is increased. This near-wall increase is counteracted by a reduction in the value of the integrand for larger $y/\ell (\theta )$ values such that the total integral remains approximately constant. This trend is found to some extent in the JHTDB bypass case, but is not as pronounced due to the shorter $Re_\theta$ extent. Thus, the Reynolds stress profiles are not self-similar, and the authors are not aware of any simple theoretical reasoning for why their integral remains a constant fraction of the skin friction coefficient, and why this constant is related to laminar boundary layer properties.

Figure 11. Integrand of the direct turbulent contribution to the local skin friction coefficient in the Wu bypass transition case. The Reynolds stresses are normalized by the local skin friction coefficient, $-\overline {u'v'}^{+} = (-\overline {u'v'}/U_\infty ^{2})/(C_f/2)$, where $C_f/2 = u_*^{2}/U_\infty ^{2}$. The wall-normal coordinate is normalized by $\ell \sim \theta$. The plotted lines extend from $Re_\theta \approx 900$ to $Re_\theta \approx 3000$. Lighter colours, and the arrows, indicate the direction of increasing of $Re_\theta$.

It is worth mentioning that similar observations about the terms in the FIK relation were made by Deck et al. (Reference Deck, Renard, Laraufie and Weiss2014). Zonal detached eddy simulations with $5200 \leqslant Re_\theta \leqslant 13\,000$ were used to show that the sum of the turbulent and laminar contributions to the skin friction coefficient as well as the streamwise growth term collapse as a function of $Re_\theta$ when normalized by the local value of $C_f$. Furthermore, the collapse of the streamwise growth term approximately matched its contribution in the Blasius boundary layer. This collapse was explained as a result of the approximate self-similarity of the total shear stress profile, which at high $Re_\tau$ is equivalent to the self-similarity of the Reynolds shear stress profile. Even though this is a possibility at asymptotically high Reynolds numbers, this does not explain why the AMI Reynolds stress integral collapses immediately after transition at our lower Reynolds numbers DNS.

Because of the empirical equality of the skin friction torque and the torque due to the Reynolds stress, it follows that the other terms in the AMI equation also cancel,

(4.3)\begin{equation} \left| \left(\frac{\partial \theta_\ell}{\partial x}-\frac{\theta-\theta_\ell}{\ell}\frac{{\rm d}\ell}{{\rm d}\kern0.06em x}\right)^{*}+\left(\frac{\theta_v}{\ell}\right)^{*}+\left(\frac{1}{Re_\ell}\right)^{*} \right| \ll 1. \end{equation}

Note that both the departure from boundary layer theory, $\mathcal {I}_{x,\ell }$, as well as the free stream pressure gradient are negligible. It is of interest to observe the apparent trends for these other three terms in order to speculate about the nature of the AMI equation in the infinite Reynolds number limit with $\ell \sim \theta$. Based on the analysis detailed in Appendix C, the laminar contribution decays to zero as $Re_\ell \rightarrow \infty$, while the mean wall-normal flux term goes to a constant. To satisfy (4.3) the streamwise growth term is negative, and decays in magnitude to a negative constant.

One of the salient features of the AMI analysis is its flexibility with respect to the choice of $\ell$, as demonstrated in § 3 for Falkner–Skan boundary layers. While $\ell \sim \theta$ proved to be the choice that collapses the direct effect of turbulence on the skin friction coefficient, another insightful choice is $\ell \sim \sqrt {x}$. This choice facilitates the comparison of a turbulent boundary layer with the Blasius boundary layer at the same $Re_x$, taking into account the fact that the turbulent history of the boundary layer makes it much thicker at a fixed $x$ location compared with the scenario in which transition and turbulence were somehow avoided. Figure 12 shows the terms in the AMI equation from the Wu transition case, normalized by the local skin friction coefficient, as a function of $Re_x$ for $\ell \sim \sqrt {x}$.

Figure 12. Terms in the AMI equation of the mean skin friction coefficient, $C_f$ in the fully developed turbulent region of the Wu transitional boundary layer, as a function of $Re_x$ with $\ell \sim \sqrt {x}$, normalized by the local value of $C_f/2$.

Using this normalization, it is evident that the torques produced by the Reynolds shear stresses and the streamwise growth of the boundary layer dominate the balance, with their difference representing the enhanced skin friction. This is due to the continual increase in the thickness of the turbulent boundary layer when compared with a laminar one due to its faster growth rate. Based on the trends observed, the Reynolds stress integral and the streamwise growth terms of the AMI equation would continue to diverge for this choice of $\ell$. Finally, for a skin friction that behaves as $C_f \sim x^{-1/5}$, the normalized laminar contribution decays as $x^{-1/3}$, and using a similar scaling analysis as that shown in Appendix C, it can be argued that the normalized contribution of the wall-normal flux of streamwise momentum deficit grows as $\sim x^{1/3}$. As such, all three non-laminar contributions are non-zero, do not disappear with increasing Reynolds numbers, and they balance intricately to match the observed wall shear stress, painting a different picture than the normalization utilizing $\ell \sim \theta$. Note that the error in closing the budget based on $\ell \sim \sqrt {x}$ was approximately $6.5\,\%$, somewhat higher than the relative error of $2\,\%$ for the $\ell \sim \theta$ analysis shown previously. This is due to the difficulty of converging the streamwise derivatives which have a larger magnitude using this choice of length scale $\ell \sim \sqrt {x}$ as opposed to when $\ell \sim \theta$ is chosen. As such, a similar relative error in the convergence of those derivatives becomes a larger error in closing the budget due to the difference in magnitudes.