Article contents
On the decay of dispersive motions in the outer region of rough-wall boundary layers
Published online by Cambridge University Press: 25 January 2019
Abstract
In rough-wall boundary layers, wall-parallel non-homogeneous mean-flow solutions exist that lead to so-called dispersive velocity components and dispersive stresses. They play a significant role in the mean-flow momentum balance near the wall, but typically disappear in the outer layer. A theoretical framework is presented to study the decay of dispersive motions in the outer layer. To this end, the problem is formulated in Fourier space, and a set of governing ordinary differential equations per mode in wavenumber space is derived by linearizing the Reynolds-averaged Navier–Stokes equations around a constant background velocity. With further simplifications, analytically tractable solutions are found consisting of linear combinations of 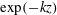 $\exp (-kz)$ and
$\exp (-kz)$ and 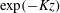 $\exp (-Kz)$, with
$\exp (-Kz)$, with  $z$ the wall distance,
$z$ the wall distance, 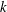 $k$ the magnitude of the horizontal wavevector
$k$ the magnitude of the horizontal wavevector 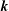 $\boldsymbol{k}$, and where
$\boldsymbol{k}$, and where 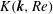 $K(\boldsymbol{k},Re)$ is a function of
$K(\boldsymbol{k},Re)$ is a function of 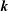 $\boldsymbol{k}$ and the Reynolds number
$\boldsymbol{k}$ and the Reynolds number 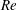 $Re$. Moreover, for
$Re$. Moreover, for 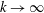 $k\rightarrow \infty$ or
$k\rightarrow \infty$ or 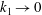 $k_{1}\rightarrow 0$ (with
$k_{1}\rightarrow 0$ (with 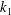 $k_{1}$ the stream-wise wavenumber),
$k_{1}$ the stream-wise wavenumber), 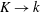 $K\rightarrow k$ is found, in which case solutions consist of a linear combination of
$K\rightarrow k$ is found, in which case solutions consist of a linear combination of 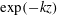 $\exp (-kz)$ and
$\exp (-kz)$ and 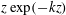 $z\exp (-kz)$, and are independent of the Reynolds number. These analytical relations are compared in the limit of
$z\exp (-kz)$, and are independent of the Reynolds number. These analytical relations are compared in the limit of 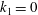 $k_{1}=0$ to the rough boundary layer experiments by Vanderwel & Ganapathisubramani (J. Fluid Mech., vol. 774, 2015, R2) and are in reasonable agreement for
$k_{1}=0$ to the rough boundary layer experiments by Vanderwel & Ganapathisubramani (J. Fluid Mech., vol. 774, 2015, R2) and are in reasonable agreement for 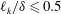 $\ell _{k}/\unicode[STIX]{x1D6FF}\leqslant 0.5$, with
$\ell _{k}/\unicode[STIX]{x1D6FF}\leqslant 0.5$, with 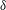 $\unicode[STIX]{x1D6FF}$ the boundary-layer thickness and
$\unicode[STIX]{x1D6FF}$ the boundary-layer thickness and 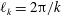 $\ell _{k}=2\unicode[STIX]{x03C0}/k$.
$\ell _{k}=2\unicode[STIX]{x03C0}/k$.
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 12
- Cited by


