Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T19:50:23.445Z Has data issue: false hasContentIssue false
  • English
  • Français

On the centrifugal effect in turbulent rotating thermal convection: onset and heat transport

Published online by Cambridge University Press:  21 March 2022

Yun-Bing Hu Open the ORCID record for Yun-Bing Hu [Opens in a new window] ,
Yi-Chao Xie Open the ORCID record for Yi-Chao Xie [Opens in a new window]  and
Ke-Qing Xia Open the ORCID record for Ke-Qing Xia [Opens in a new window]
Yun-Bing Hu
Affiliation:
Center for Complex Flows and Soft Matter Research, and Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, PR China
Yi-Chao Xie
Affiliation:
State Key Laboratory for Strength and Vibration of Mechanical Structures, and School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, PR China
Ke-Qing Xia*
Affiliation:
Center for Complex Flows and Soft Matter Research, and Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of centrifugal force in turbulent rotating Rayleigh–Bénard convection (RRBC) is studied experimentally in an aspect-ratio $\varGamma =1$ cylindrical convection cell and in the ranges of the Froude number $0.004\leq Fr \leq 0.363$ and the Rayleigh number $2.8\times 10^8 \leq Ra \leq 9.5\times 10^9$, and with the Prandtl number fixed at $Pr=4.34$. We use the bulk temperature anomaly to determine the onset Froude number $Fr_c$, beyond which the centrifugal effects cannot be regarded as insignificant. It is found that $Fr_c$ depends on $Ra$ as $Fr_c\sim Ra^{0.53}$, which may be understood qualitatively by the idea of local force balance. 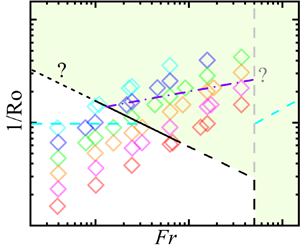For $Fr>Fr_c$, the centrifugal effect is more pronounced for smaller $Ra$, which is also found for larger constant $1/Ro$. This implies that the response of the system to the centrifugal force depends on the flow states, which, in RRBC, is mainly determined by the competition between the buoyancy and Coriolis forces. Detailed analysis of the sidewall temperature signal shows results consistent with those obtained from the bulk temperature. Based on the above results, we propose a different division of the $1/Ro$–$Fr$ phase space than previously suggested. For the heat transport, the results under fixed $1/Ro$ show well-defined $Nu$–$Ra$ scalings, which can provide a better prediction for the heat transport when extrapolating to the unexplored regions in the phase space.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 938 , 10 May 2022 , R1
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Brown, E., Araujo, F.F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006 Non-Oberbeck-Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.CrossRefGoogle Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Courier Corporation.Google Scholar
Cheng, J.S., Madonia, M., Aguirre Guzmán, A.J. & Kunnen, R.P.J. 2020 Laboratory exploration of heat transfer regimes in rapidly rotating turbulent convection. Phys. Rev. Fluids 5, 113501.CrossRefGoogle Scholar
Chong, K.-L., Shi, J.-Q., Ding, G.-Y., Ding, S.-S., Lu, H.-Y., Zhong, J.-Q. & Xia, K.-Q. 2020 Vortices as Brownian particles in turbulent flows. Sci. Adv. 6, eaaz1110.CrossRefGoogle ScholarPubMed
Curbelo, J., Lopez, J.M., Mancho, A.M. & Marques, F. 2014 Confined rotating convection with large Prandtl number: centrifugal effects on wall modes. Phys. Rev. E 89, 013019.CrossRefGoogle ScholarPubMed
Ding, S.-S., Chong, K.-L., Shi, J.-Q., Ding, G.-Y., Lu, H.-Y., Xia, K.-Q. & Zhong, J.-Q. 2021 Inverse centrifugal effect induced by collective motion of vortices in rotating thermal convection. Nat. Commun. 12, 5585.CrossRefGoogle ScholarPubMed
Favier, B. & Knobloch, E. 2020 Robust wall states in rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 895, R1.CrossRefGoogle Scholar
Horn, S. & Aurnou, J.M. 2018 Regimes of coriolis-centrifugal convection. Phys. Rev. Lett. 120, 204502.CrossRefGoogle ScholarPubMed
Horn, S. & Aurnou, J.M. 2019 Rotating convection with centrifugal buoyancy: numerical predictions for laboratory experiments. Phys. Rev. Fluids 4, 073501.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck-Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26, 055111.CrossRefGoogle Scholar
Hu, Y.-B., Huang, S.-D., Xie, Y.-C. & Xia, K.-Q. 2021 Centrifugal-force-induced flow bifurcations in turbulent thermal convection. Phys. Rev. Lett. 127, 244501.CrossRefGoogle ScholarPubMed
Hughes, D.W. 2003 Planetary spin. Planet. Space Sci. 51, 517–523.CrossRefGoogle Scholar
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.CrossRefGoogle Scholar
Kaspi, Y., et al. 2018 Jupiter's atmospheric jet streams extend thousands of kilometres deep. Nature 555, 223.CrossRefGoogle ScholarPubMed
Kunnen, R.P.J. 2021 The geostrophic regime of rapidly rotating turbulent convection. J. Turbul. 22, 267–296.CrossRefGoogle Scholar
Kunnen, R.P.J., Geurts, B.J. & Clercx, H.J.H. 2009 Turbulence statistics and energy budget in rotating Rayleigh–Bénard convection. Eur. J. Mech. B/Fluids 28, 578–589.CrossRefGoogle Scholar
Kunnen, R.P.J., Stevens, R.J.A.M., Overkamp, J., Sun, C., van Heijst, G.F. & Clercx, H.J.H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.CrossRefGoogle Scholar
Liu, Y. & Ecke, R.E. 1997 Heat transport scaling in turbulent Rayleigh–Bénard convection: effects of rotation and Prandtl number. Phys. Rev. Lett. 79, 2257–2260.CrossRefGoogle Scholar
Liu, Y. & Ecke, R.E. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80, 036314.CrossRefGoogle ScholarPubMed
Lopez, J.M., Rubio, A. & Marques, F. 2006 Travelling circular waves in axisymmetric rotating convection. J. Fluid Mech. 569, 331–348.CrossRefGoogle Scholar
Marques, F., Mercader, I., Batiste, O. & Lopez, J.M. 2007 Centrifugal effects in rotating convection: axisymmetric states and three-dimensional instabilities. J. Fluid Mech. 580, 303–318.CrossRefGoogle Scholar
Nieves, D., Rubio, A.M. & Julien, K. 2014 Statistical classification of flow morphology in rapidly rotating Rayleigh–Bénard convection. Phys. Fluids 26, 086602.CrossRefGoogle Scholar
Noto, D., Tasaka, Y., Yanagisawa, T. & Murai, Y. 2019 Horizontal diffusive motion of columnar vortices in rotating Rayleigh-Bénard convection. J. Fluid Mech. 871, 401–426.CrossRefGoogle Scholar
Snellen, I.A.G., Brandl, B.R., de Kok, R.J., Brogi, M., Birkby, J. & Schwarz, H. 2014 Fast spin of the young extrasolar planet $\beta$ Pictoris b. Nature 509, 63–65.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.CrossRefGoogle Scholar
Stevens, R.J.A.M., Clercx, H.J.H. & Lohse, D. 2013 Heat transport and flow structure in rotating Rayleigh–Bénard convection. Eur. J. Mech. B/Fluids 40, 41–49.CrossRefGoogle Scholar
Weiss, S. & Ahlers, G. 2011 The large-scale flow structure in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 461–492.CrossRefGoogle Scholar
Weiss, S., Wei, P. & Ahlers, G. 2016 Heat-transport enhancement in rotating turbulent Rayleigh–Bénard convection. Phys. Rev. E 93, 043102.CrossRefGoogle ScholarPubMed
de Wit, X.M., Guzmán, A.J.A., Madonia, M., Cheng, J.S., Clercx, H.J.H. & Kunnen, R.P.J. 2020 Turbulent rotating convection confined in a slender cylinder: the sidewall circulation. Phys. Rev. Fluids 5, 023502.CrossRefGoogle Scholar
Zhang, X., van Gils, D.P.M., Horn, S., Wedi, M., Zwirner, L., Ahlers, G., Ecke, R.E., Weiss, S., Bodenschatz, E. & Shishkina, O. 2020 Boundary zonal flow in rotating turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 124, 084505.CrossRefGoogle ScholarPubMed
Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.CrossRefGoogle Scholar
Zhong, J.-Q., Stevens, R.J.A.M., Clercx, H.J.H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.CrossRefGoogle ScholarPubMed