Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T23:14:29.688Z Has data issue: false hasContentIssue false
  • English
  • Français

On the bubble shape in a magnetically compensated gravity environment

Published online by Cambridge University Press:  29 January 2013

Jérôme Duplat  and
Alain Mailfert
Jérôme Duplat*
Affiliation:
SBT, UMR-E 9004 CEA / UJF-Grenoble 1, INAC, Grenoble, F-38054, France
Alain Mailfert
Affiliation:
Labo Géoressources, Lorraine University – CNRS, ENSG Vandoeuvre-lès-Nancy, F-54500, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the shape of bubbles in liquid oxygen under magnetic levitation conditions: a magnetic field is applied that polarizes bulk oxygen, and its spatial variation induces a body force opposed to its weight. In these conditions, bubbles appear to have a smooth ellipsoidal shape, which may be prolate (elongated in the vertical direction), oblate (elongated in the horizontal plane) or perfectly spherical. 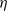The dependence of the elongation ratio $\eta $ on the volume and levitation position is explored. It is found that the bubble shape is prescribed by the minimization of the sum of surface tension, demagnetization and magnetic–gravitational potential energies.

JFM classification

Drops and Bubbles: Drops and Bubbles Drops and Bubbles: Electrohydrodynamic effects MHD and Electrohydrodynamics: Magnetic fluids
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , R11
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Archipenko, V. I., Barkov, Yu. D. & Bashtovoi, V. G. 1979 Shape of a drop of magnetized fluid in homogeneous magnetic field. Magnetohydrodynamics 14 (3), 373–375.Google Scholar
Bacri, J. C. & Salin, D. 1982 Instability of ferrofluid magnetic drops under magnetic field. J. Phys. Lett. 43, L649–L654.CrossRefGoogle Scholar
Banerjee, S., Fasnacht, M., Garoff, S. & Widom, M. 1999 Elongation of confined ferrofluid droplets under applied fields. Phys. Rev. E 60, 4272–4279.CrossRefGoogle ScholarPubMed
Braunbek, W. 1939 Freies Schweben diamagnetischer Körper im Magnetfeld. Z. Phys. A: Hadrons Nuclei 112 (11), 764–769.CrossRefGoogle Scholar
Cowley, M. D. & Rosensweig, R. E. 1967 The interfacial stability of a ferromagnetic fluid. J. Fluid Mech. 30 (4), 671–688.CrossRefGoogle Scholar
Flament, C., Lacis, S., Bacri, J.-C., Cebers, A., Neveu, S. & Perzynski, R. 1996 Measurements of ferrofluids surface tension in confined geometry. Phys. Rev. E 53, 4801–4806.CrossRefGoogle ScholarPubMed
Fournet, G. 1979 Électromagnétisme. Masson.Google Scholar
de Gennes, P. G., Brochard-Wyart, F., Quéré, D., Fermigier, M. & Clanet, C. 2002 Gouttes, Bulles, Perles et Ondes. Belin.Google Scholar
Kirichenko, Y. A. & Verkin, B. I. 1968 Simulation of zero and reduced gravity fields for heat transfer investigations under boiling. Dopov. Akad. Nauk Ukr. SSR, Ser. A 7, 637–640.Google Scholar
Lide, D. R. (Ed.) 2005 Handbook of Chemistry and Physics, 86th edn. CRC, Taylor & Francis.Google Scholar
Lorin, C. & Mailfert, A. 2009 Magnetic compensation of gravity and centrifugal forces. Microgravity Sci. Technol. 21 (1–2), 123–127.CrossRefGoogle Scholar
Lorin, C., Mailfert, A., Chatain, D., Félice, H. & Beysens, D. 2009 Magnetogravitational potential revealed near a liquid-vapour critical point. J. Appl. Phys. 106 (3)033905.CrossRefGoogle Scholar
Lyon, D. N., Jones, M. C., Ritter, G. L., Chiladakis, C. I. & Kosky, P. G. 1965 Peak nucleate boiling fluxes for liquid oxygen on a flat horizontal platinum surface at buoyancies corresponding to accelerations between $- 0. 03$ and 1 ${g}_{E} $ . AIChE J. 11 (5), 773–780.CrossRefGoogle Scholar
Nikolayev, V. S., Chatain, D., Beysens, D. & Pichavant, G. 2011 Magnetic gravity compensation. Microgravity Sci. Technol. 23 (2), 113–122.CrossRefGoogle Scholar
Osborn, J. A. 1945 Demagnetizing factors of the general ellipsoid. Phys. Rev. 67 (11–12), 351–357.CrossRefGoogle Scholar
Pichavant, G., Cariteau, B., Chatain, D., Nikolayev, V. & Beysens, D. 2009 Magnetic compensation of gravity: experiments with oxygen. Microgravity Sci. Technol. 21 (1), 129–133.CrossRefGoogle Scholar
Piroird, K., Darbois Texier, B., Clanet, C. & Quéré, D. 2012 Shaping and capturing leidenfrost drops with a magnetic field. Phys. Fluids, arXiv:1210.5718v1.Google Scholar
Quettier, L., Félice, H., Mailfert, A., Chatain, D. & Beysens, D. 2005 Magnetic compensation of gravity forces in liquid/gas mixtures: surpassing intrinsic limitations of a superconducting magnet by using ferromagnetic inserts. Eur. Phys. J. Appl. Phys. 32, 167–175.CrossRefGoogle Scholar
Rosensweig, R. E. 1985 Ferrohydrodynamics. Dover.Google Scholar
Stone, H. A., Lister, J. R. & Brenner, M. P. 1999 Drops with conical ends in electric and magnetic fields. Proc. R. Soc. Lond. A 455 (1981), 329–347.CrossRefGoogle Scholar
Weilert, M. A., Whitaker, D. L., Maris, H. J. & Seidel, G. M. 1996 Magnetic levitation and noncoalescence of liquid helium. Phys. Rev. Lett. 77 (23), 4840–4843.CrossRefGoogle ScholarPubMed