Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Murugan, Sugan Durai
Frisch, Uriel
Nazarenko, Sergey
Besse, Nicolas
and
Ray, Samriddhi Sankar
2020.
Suppressing thermalization and constructing weak solutions in truncated inviscid equations of hydrodynamics: Lessons from the Burgers equation.
Physical Review Research,
Vol. 2,
Issue. 3,
Yao, Jie
and
Hussain, Fazle
2020.
Separation scaling for viscous vortex reconnection.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Mishra, Aakash
Pumir, Alain
and
Ostilla-Mónico, Rodolfo
2021.
Instability and disintegration of vortex rings during head-on collisions and wall interactions.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Moffatt, H.K.
2021.
Some topological aspects of fluid dynamics.
Journal of Fluid Mechanics,
Vol. 914,
Issue. ,
Tao, Rui
Ren, Hongxiang
Tong, Yunjin
and
Xiong, Shiying
2021.
Construction and evolution of knotted vortex tubes in incompressible Schrödinger flow.
Physics of Fluids,
Vol. 33,
Issue. 7,
Yao, Jie
and
Hussain, Fazle
2021.
Polarized vortex reconnection.
Journal of Fluid Mechanics,
Vol. 922,
Issue. ,
Zhao, Xinran
Yu, Zongxin
Chapelier, Jean-Baptiste
and
Scalo, Carlo
2021.
Direct numerical and large-eddy simulation of trefoil knotted vortices.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Ostilla-Mónico, Rodolfo
McKeown, Ryan
Brenner, Michael P.
Rubinstein, Shmuel M.
and
Pumir, Alain
2021.
Cascades and reconnection in interacting vortex filaments.
Physical Review Fluids,
Vol. 6,
Issue. 7,
Yao, Jie
Yang, Yue
and
Hussain, Fazle
2021.
Dynamics of a trefoil knotted vortex.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Hu, J.
and
Peterson, S. D.
2021.
The influence of collision angle for viscous vortex reconnection.
Physics of Fluids,
Vol. 33,
Issue. 9,
Yao, Jie
and
Hussain, Fazle
2022.
Vortex Reconnection and Turbulence Cascade.
Annual Review of Fluid Mechanics,
Vol. 54,
Issue. 1,
p.
317.
Dou, Hua-Shu
2022.
Origin of Turbulence.
p.
105.
Shen, Weiyu
Yao, Jie
Hussain, Fazle
and
Yang, Yue
2022.
Topological transition and helicity conversion of vortex knots and links.
Journal of Fluid Mechanics,
Vol. 943,
Issue. ,
Cheminet, Adam
Geneste, Damien
Barlet, Antoine
Ostovan, Yasar
Chaabo, Tarek
Valori, Valentina
Debue, Paul
Cuvier, Christophe
Daviaud, François
Foucaut, Jean-Marc
Laval, Jean-Philippe
Padilla, Vincent
Wiertel-Gasquet, Cécile
and
Dubrulle, Bérengère
2022.
Eulerian vs Lagrangian Irreversibility in an Experimental Turbulent Swirling Flow.
Physical Review Letters,
Vol. 129,
Issue. 12,
Van Gorder, Robert A.
2022.
Finite time blowup of incompressible flows surrounding compressible bubbles evolving under soft equations of state.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 478,
Issue. 2262,
Faller, Hugues
Fery, Lucas
Geneste, Damien
and
Dubrulle, Bérengère
2022.
A Model of Interacting Navier–Stokes Singularities.
Entropy,
Vol. 24,
Issue. 7,
p.
897.
Dou, Hua-Shu
2022.
No Existence and Smoothness of Solution of the Navier-Stokes Equation.
Entropy,
Vol. 24,
Issue. 3,
p.
339.
Yao, Jie
Shen, Weiyu
Yang, Yue
and
Hussain, Fazle
2022.
Helicity dynamics in viscous vortex links.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Harikrishnan, Abhishek
Rodal, Marie
Klein, Rupert
Margerit, Daniel
and
Vercauteren, Nikki
2023.
On the motion of hairpin filaments in the atmospheric boundary layer.
Physics of Fluids,
Vol. 35,
Issue. 7,
Hu, JiaCheng
and
Peterson, Sean D.
2023.
Inviscid evolution of a uniform vortex dipole in a strain field.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
 $R$. The separation between the two tipping points
$R$. The separation between the two tipping points  $2s_{0}$ and the scale of the core cross-section
$2s_{0}$ and the scale of the core cross-section  $\unicode[STIX]{x1D6FF}_{0}$ are chosen as
$\unicode[STIX]{x1D6FF}_{0}$ are chosen as  $\unicode[STIX]{x1D6FF}_{0}=0.1s_{0}=0.01R$; the vortex Reynolds number (
$\unicode[STIX]{x1D6FF}_{0}=0.1s_{0}=0.01R$; the vortex Reynolds number ( $Re=\text{circulation/viscosity}$) ranges from 1000 to 4000. In contrast to the claim that the core remains compact and circular, there is notable core flattening and stripping, which further increases with
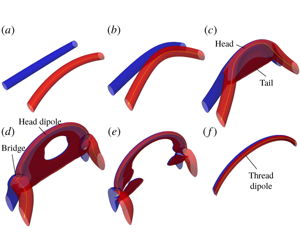
$Re=\text{circulation/viscosity}$) ranges from 1000 to 4000. In contrast to the claim that the core remains compact and circular, there is notable core flattening and stripping, which further increases with  $Re$ – akin to our previous finding in the standard anti-parallel vortex reconnection. Furthermore, the induced motion of bridges arrests the curvature growth and vortex stretching at the tipping points; consequently, the maximum vorticity grows with
$Re$ – akin to our previous finding in the standard anti-parallel vortex reconnection. Furthermore, the induced motion of bridges arrests the curvature growth and vortex stretching at the tipping points; consequently, the maximum vorticity grows with  $Re$ substantially slower than the exponential scaling predicted by the model – implying that, for this configuration, even physical singularity is unlikely. Our simulations not only shed light on the longstanding question of finite-time singularities, but also further delineate the detailed mechanisms of reconnection. In particular, we show for the first time that the separation distance
$Re$ substantially slower than the exponential scaling predicted by the model – implying that, for this configuration, even physical singularity is unlikely. Our simulations not only shed light on the longstanding question of finite-time singularities, but also further delineate the detailed mechanisms of reconnection. In particular, we show for the first time that the separation distance  $s(\unicode[STIX]{x1D70F})$ before reconnection follows 1/2 scaling exactly – a significant DNS result.
$s(\unicode[STIX]{x1D70F})$ before reconnection follows 1/2 scaling exactly – a significant DNS result.