Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T10:44:23.942Z Has data issue: false hasContentIssue false
  • English
  • Français

On shock-induced heavy-fluid-layer evolution

Published online by Cambridge University Press:  08 June 2021

Yu Liang Open the ORCID record for Yu Liang [Opens in a new window]  and
Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window]
Yu Liang*
Affiliation:
NYUAD Research Institute, New York University Abu Dhabi, Abu Dhabi129188, UAE Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, PR China
Xisheng Luo*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

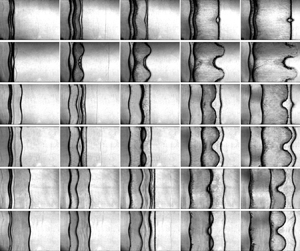
Investigation on the shock-induced finite-thickness fluid-layer evolution is very desirable but remains a challenge because it not only involves both the Richtmyer–Meshkov instability (RMI) and the Rayleigh–Taylor instability (RTI), but also strongly depends on the waves reverberated inside the layer. We experimentally and theoretically examined the evolution of a shocked $\textrm {SF}_6$ gas layer with a finite thickness surrounded by air. Specifically, three kinds of quasi-one-dimensional $\textrm {SF}_6$ gas layers with different layer thicknesses are generated to study the wave patterns and interface motions, and six types of quasi-two-dimensional $\textrm {SF}_6$ gas layers with diverse layer thicknesses and amplitude combinations are created to explore the interfacial instabilities of the layer. When the initial fluid layer is thin, the two interfaces of the layer coalesce at a late time. The present study is the first to report that except for the RMI induced by a shock wave on the two interfaces, the rarefaction waves (RW) inside the fluid layer induce the additional RTI and decompression effect on the first interface, and the compression waves (CW) inside the fluid layer cause the additional Rayleigh–Taylor stabilisation (RTS) and compression effect on the second interface. A general one-dimensional theory is established to describe the motions of the two interfaces. Linear and nonlinear models are successfully established by considering the interface-coupling effect on the RMI and the additional interfacial instabilities induced by these waves inside the heavy fluid layer. The established models predict well the perturbation growths on the two interfaces at all regimes.

JFM classification

Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A13
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Banerjee, A. 2020 Rayleigh–Taylor instability: a status review of experimental designs and measurement diagnostics. Trans. ASME J. Fluids Engng 142 (12), 120801.CrossRefGoogle Scholar
Bell, G.I. 1951 Taylor instability on cylinders and spheres in the small amplitude approximation. Rep. No. LA-1321, LANL 1321.Google Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Budzinski, J.M., Benjamin, R.F. & Jacobs, J.W. 1994 Influence of initial conditions on the flow patters of a shock-accelerated thin fluid layer. Phys. Fluids 6, 3510–3512.CrossRefGoogle Scholar
Dimonte, G. & Ramaprabhu, P. 2010 Simulations and model of the nonlinear Richtmyer–Meshkov instability. Phys. Fluids 22, 014104.CrossRefGoogle Scholar
Ding, J., Li, J., Sun, R., Zhai, Z. & Luo, X. 2019 Convergent Richtmyer–Meshkov instability of a heavy gas layer with perturbed outer interface. J. Fluid Mech. 878, 277–291.CrossRefGoogle Scholar
Drake, R.P. 2018 High-Energy-Density Physics: Foundation of Inertial Fusion and Experimental Astrophysics. Springer.CrossRefGoogle Scholar
de Frahan, M.T.H., Movahed, P. & Johnsen, E. 2015 Numerical simulations of a shock interacting with successive interfaces using the discontinuous galerkin method: the multilayered Richtmyer–Meshkov and Rayleigh–Taylor instabilities. Shock Waves 25 (4), 329–345.CrossRefGoogle Scholar
Han, Z. & Yin, X. 1993 Shock Dynamics. Kluwer Academic Publishers and Science Press.CrossRefGoogle Scholar
Jacobs, J.W., Jenkins, D.G., Klein, D.L. & Benjamin, R.F. 1995 Nonlinear growth of the shock-accelerated instability of a thin fluid layer. J. Fluid Mech. 295, 23–42.CrossRefGoogle Scholar
Jacobs, J.W., Klein, D.L., Jenkins, D.G. & Benjamin, R.F. 1993 Instability growth patterns of a shock-accelerated thin fluid layer. Phys. Rev. Lett. 70, 583–586.CrossRefGoogle ScholarPubMed
Kuranz, C.C., et al. , 2018 How high energy fluxes may affect Rayleigh–Taylor instability growth in young supernova remnants. Nat. Commun. 9, 1564.CrossRefGoogle ScholarPubMed
Li, J., Ding, J., Si, T. & Luo, X. 2020 Convergent Richtmyer–Meshkov instability of light gas layer with perturbed outer surface. J. Fluid Mech. 884, R2.CrossRefGoogle Scholar
Liang, Y., Liu, L., Zhai, Z., Si, T. & Wen, C.-Y. 2020 a Evolution of shock-accelerated heavy gas layer. J. Fluid Mech. 886, A7.CrossRefGoogle Scholar
Liang, Y., Zhai, Z., Ding, J. & Luo, X. 2019 Richtmyer–Meshkov instability on a quasi-single-mode interface. J. Fluid Mech. 872, 729–751.CrossRefGoogle Scholar
Liang, Y., Zhai, Z., Luo, X. & Wen, C. 2020 b Interfacial instability at a heavy/light interface induced by rarefaction waves. J. Fluid Mech. 885, A42.CrossRefGoogle Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.CrossRefGoogle Scholar
Liu, L., Liang, Y., Ding, J., Liu, N. & Luo, X. 2018 a An elaborate experiment on the single-mode Richtmyer–Meshkov instability. J. Fluid Mech. 853, R2.CrossRefGoogle Scholar
Liu, W., Li, X., Yu, C., Fu, Y., Wang, P., Wang, L. & Ye, W. 2018 b Theoretical study on finite-thickness effect on harmonics in Richtmyer–Meshkov instability for arbitrary Atwood numbers. Phys. Plasmas 25 (12), 122103.CrossRefGoogle Scholar
Luo, X., Liang, Y., Si, T. & Zhai, Z. 2019 Effects of non-periodic portions of interface on Richtmyer–Meshkov instability. J. Fluid Mech. 861, 309–327.CrossRefGoogle Scholar
Luo, X., Zhang, F., Ding, J., Si, T., Yang, J., Zhai, Z. & Wen, C. 2018 Long-term effect of Rayleigh–Taylor stabilization on converging Richtmyer–Meshkov instability. J. Fluid Mech. 849, 231–244.CrossRefGoogle Scholar
Meshkov, E.E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.CrossRefGoogle Scholar
Meyer, K.A. & Blewett, P.J. 1972 Numerical investigation of the stability of a shock-accelerated interface between two fluids. Phys. Fluids 15, 753–759.CrossRefGoogle Scholar
Mikaelian, K.O. 1982 Normal modes and symmetries of the Rayleigh–Taylor instability in stratified fluids. Phys. Rev. Lett. 48 (19), 1365.CrossRefGoogle Scholar
Mikaelian, K.O. 1985 Richtmyer–Meshkov instabilities in stratified fluids. Phys. Rev. A 31, 410–419.CrossRefGoogle ScholarPubMed
Mikaelian, K.O. 1990 Rayleigh–Taylor and Richtmyer–Meshkov instabilities in multilayer fluids with surface tension. Phys. Rev. A 42 (12), 7211.CrossRefGoogle ScholarPubMed
Mikaelian, K.O. 1995 Rayleigh–Taylor and Richtmyer–Meshkov instabilities in finite-thickness fluid layers. Phys. Fluids 7 (4), 888–890.CrossRefGoogle Scholar
Mikaelian, K.O. 1996 Numerical simulations of Richtmyer–Meshkov instabilities in finite-thickness fluid layers. Phys. Fluids 8 (5), 1269–1292.CrossRefGoogle Scholar
Morgan, R.V., Cabot, W.H., Greenough, J.A. & Jacobs, J.W. 2018 Rarefaction-driven Rayleigh–Taylor instability. Part 2. Experiments and simulations in the nonlinear regime. J. Fluid Mech. 838, 320–355.CrossRefGoogle Scholar
Morgan, R.V., Likhachev, O.A. & Jacobs, J.W. 2016 Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory. J. Fluid Mech. 791, 34–60.CrossRefGoogle Scholar
Olmstead, D., Wayne, P., Yoo, J.-H., Kumar, S., Truman, C.R. & Vorobieff, P. 2017 Experimental study of shock-accelerated inclined heavy gas cylinder. Exp. Fluids 58 (6), 71.CrossRefGoogle Scholar
Ott, E. 1972 Nonlinear evolution of the Rayleigh–Taylor instability of a thin layer. Phys. Rev. Lett. 29 (21), 1429.CrossRefGoogle Scholar
Plesset, M.S. 1954 On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.CrossRefGoogle Scholar
Prestridge, K., Vorobieff, P., Rightley, P.M. & Benjamin, R.F. 2000 Validation of an instability growth model using particle image velocimtery measurement. Phys. Rev. Lett. 84, 4353–4356.CrossRefGoogle Scholar
Rayleigh, L. 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Richtmyer, R.D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.CrossRefGoogle Scholar
Romero, B.E., Poroseva, S., Vorobieff, P. & Reisner, J. 2021 Shock driven Kelvin–Helmholtz instability. In AIAA Scitech 2021 Forum, p. 0051. AIAA.CrossRefGoogle Scholar
Sharp, D.H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12 (1), 3–18.CrossRefGoogle Scholar
Sun, R., Ding, J., Zhai, Z., Si, T. & Luo, X. 2020 Convergent Richtmyer–Meshkov instability of heavy gas layer with perturbed inner surface. J. Fluid Mech. 902, A3.CrossRefGoogle Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Velikovich, A. & Phillips, L. 1996 Instability of a plane centered rarefaction wave. Phys. Fluids 8 (4), 1107–1118.CrossRefGoogle Scholar
Wang, L., Guo, H., Wu, J., Ye, W., Liu, J., Zhang, W. & He, X. 2014 Weakly nonlinear Rayleigh–Taylor instability of a finite-thickness fluid layer. Phys. Plasmas 21 (12), 122710.Google Scholar
Zhai, Z., Zou, L., Wu, Q. & Luo, X. 2018 Review of experimental Richtmyer–Meshkov instability in shock tube: from simple to complex. Proc. Inst. Mech. Engrs 232, 2830–2849.Google Scholar
Zhang, Q. & Guo, W. 2016 Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios. J. Fluid Mech. 786, 47–61.CrossRefGoogle Scholar
Zhou, Y. 2017 a Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar
Zhou, Y. 2017 b Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 723–725, 1–160.Google Scholar