Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T09:14:19.898Z Has data issue: false hasContentIssue false
  • English
  • Français

On new scaling laws in a temporally evolving turbulent plane jet using Lie symmetry analysis and direct numerical simulation

Published online by Cambridge University Press:  06 September 2018

H. Sadeghi Open the ORCID record for H. Sadeghi [Opens in a new window] ,
M. Oberlack  and
M. Gauding
H. Sadeghi*
Affiliation:
Chair of Fluid Dynamics, Department of Mechanical Engineering, TU Darmstadt, Germany
M. Oberlack
Affiliation:
Chair of Fluid Dynamics, Department of Mechanical Engineering, TU Darmstadt, Germany Centre for Computational Engineering, TU Darmstadt, Germany
M. Gauding
Affiliation:
CORIA, CNRS UMR 6614, Saint Etienne du Rouvray, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A temporally evolving turbulent plane jet is studied both by direct numerical simulation (DNS) and Lie symmetry analysis. The DNS is based on a high-order scheme to solve the Navier–Stokes equations for an incompressible fluid. Computations were conducted at Reynolds number 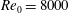$\mathit{Re}_{0}=8000$, where 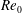$\mathit{Re}_{0}$ is defined based on the initial jet thickness, 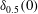$\unicode[STIX]{x1D6FF}_{0.5}(0)$, and the initial centreline velocity, 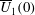$\overline{U}_{1}(0)$. A symmetry approach, known as the Lie group, is used to find symmetry transformations, and, in turn, group invariant solutions, which are also denoted as scaling laws in turbulence. This approach, which has been extensively developed to create analytical solutions of differential equations, is presently applied to the mean momentum and two-point correlation equations in a temporally evolving turbulent plane jet. The symmetry analysis of these equations allows us to derive new invariant (self-similar) solutions for the mean flow and higher moments of the velocities in the jet flow. The current DNS validates the consequence of Lie symmetry analysis and therefore confirms the establishment of novel scaling laws in turbulence. It is shown that the classical scaling law for the mean velocity is a specific form of the current scaling (which has a more general form); however, the scaling for the second and higher moments (such as Reynolds stresses) has a completely different structure compared to the classical scaling. While the failure of the classical scaling for the second moments of the fluctuating velocities has been noted from the jet data for many years, the DNS results nicely match with the present self-similar relations derived from Lie symmetry analysis. Key ingredients for the present results, in particular for the scaling laws of the higher moments, are symmetries, which are of a purely statistical nature. i.e. these symmetries are admitted by the moment equations, however, they are not observed by the original Navier–Stokes equations.

JFM classification

Wakes/Jets: Jets Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 233 - 260
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonio, A. & Fabrizio, B. 2012 Statistics and scaling of turbulence in a spatially developing mixing layer at Re𝜆 = 250. Phys. Fluids 24, 035109.Google Scholar
Antonia, R. A., Satyaprakash, B. A. & Hussain, A. K. F. M. 1980 Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets. Phys. Fluids 23, 695–700.Google Scholar
Avsarkisov, V., Oberlack, M. & Hoyas, S. 2014 New scaling laws for turbulent Poiseuille flow with wall transpiration. J. Fluid Mech. 746, 99–122.Google Scholar
Bluman, G. W. 1990 Simplifying the form of lie groups admitted by a given differential equation. J. Math. Anal. Appl. 145, 52–62.Google Scholar
Bluman, G. W., Cheviakov, A. F. & Anco, S. C. 2010 Applications of Symmetry Methods to Partial Differential Equations. Springer.Google Scholar
Bradbury, L. J. S. 1965 The structure of a self-preserving turbulent plane jet. J. Fluid Mech. 23, 31–64.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005 Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.Google Scholar
Cheviakov, A. F. 2007 Gem software package for computation of symmetries and conservation laws of differential equations. Comput. Phys. Commun. 176, 48–61.Google Scholar
Djenidi, L. & Antonia, R. A. 2015 A general self-preservation analysis for decaying homogeneous isotropic turbulence. J. Fluid Mech. 773, 345–365.Google Scholar
Ewing, D., Frohnapfel, B., Pedersen, W. K., George, J. M. & Westerweel, J. 2007 Two-point similarity in the round jet. J. Fluid Mech. 577, 309–330.Google Scholar
Gampert, M., Boschung, J., Hennig, F., Gauding, M. & Peters, N. 2014 The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface. J. Fluid Mech. 750, 578–596.Google Scholar
Gauding, M., Goebbert, J. H., Hasse, C. & Peters, N. 2015 Line segments in homogeneous scalar turbulence. Phys. Fluids 27 (9), 095102.Google Scholar
George, W. K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. In Advances in Turbulence (ed. George, W. K. & Arndt, R.). Springer.Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids 4 (7), 1492–1509.Google Scholar
George, W. K. 2012 Asymptotic effect of initial and upstream conditions on turbulence. Trans. ASME J. Fluids Engng 134, 061203.Google Scholar
George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.Google Scholar
George, W. K. & Davidson, L. 2004 Role of initial conditions in establishing asymptotic flow behavior. AIAA J. 42, 438–446.Google Scholar
George, W. K. & Wang, H. 2009 The exponential decay of homogeneous turbulence. Phys. Fluids 21, 025108.Google Scholar
Ghosal, S. & Rogers, M. M. 1997 A numerical study of self-similarity in a turbulent plane wake using large eddy simulation. Phys. Fluids 9, 1729–1739.Google Scholar
Gutmark, E. & Wygnanski, I. 1976 The planar turbulent jet. J. Fluid Mech. 73, 465–495.Google Scholar
Heskestad, G. 1965 Hot-wire measurements in a plane turbulent jet. Trans. ASME J. Appl. Mech. 32, 721–734.Google Scholar
Hinze, O. J. 1959 Turbulence, An Introduction to its Mechanism and Theory. McGraw-Hill.Google Scholar
Hunger, F., Gauding, M. & Hasse, C. 2016 On the impact of the turbulent/non-turbulent interface on differential diffusion in a turbulent jet flow. J. Fluid Mech. 802, R5.Google Scholar
Hydon, P. E. 2000 Symmetry Methods for Differential Equations: A Beginner’s Guide. Cambridge University Press.Google Scholar
Keller, L. & Friedmann, A. 1924 Differentialgleichungen für die turbulente Bewegung einer kompressiblen Flüssigkeit. In First. Intl Congr. Appl. Mech. (ed. Biezeno, C. B. & Burgers, J. M.), pp. 395–405. Delft.Google Scholar
Khabirov, S. V. & Unal, G. 2002a Group analysis of the von Karman and Howarth equation. Part I. Submodels. Commun. Nonlinear Sci. Numer. Simul. 7, 3–18.Google Scholar
Khabirov, S. V. & Unal, G. 2002b Group analysis of the von Karman and Howarth equation. Part II. Physical invariant solutions. Commun. Nonlinear Sci. Numer. Simul. 7, 19–30.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.Google Scholar
Moser, R. D., Roger, M. M. & Ewing, D. W. 1998 Self-similarity of time-evolving plane wakes. J. Fluid Mech. 367, 255–289.Google Scholar
Oberlack, M.2000 Symmetrie, invarianz und selbstähnlichkeit in der turbulenz. PhD thesis, Habilitation thesis.Google Scholar
Oberlack, M. 2001 A unified approach for symmetries in plane parallel turbulent shear flows. J. Fluid Mech. 427, 299–328.Google Scholar
Oberlack, M. 2002 Symmetries and invariant solutions of turbulent flows and their implications for turbulence modelling. In Theories of Turbulence. Springer.Google Scholar
Oberlack, M. & Guenther, S. 2003 Shear-free turbulent dffiusion-classical and new scaling laws. Fluid Dyn. Res. 33, 453–476.Google Scholar
Oberlack, M. & Rosteck, A. 2010 New statistical symmetries of the multi-point equations and its importance for turbulent scaling laws. Discrete Contin. Dyn. Syst. 3, 451–471.Google Scholar
Oberlack, M. & Rosteck, A. 2011 Applications of the new symmetries of the multi-point correlation equations. J. Phys. 318, 042011.Google Scholar
Oberlack, M., Waclawczyk, M., Rosteck, A. & Avsarkisov, V. 2015 Symmetries and their importance for statistical turbulence theory. Mech. Engng Rev. 2, 1–72.Google Scholar
Oberlack, M. & Zieleniewicz, M. 2013 Statistical symmetries and its impact on new decay modes and integral invariants of decaying turbulence. J. Turbul. 14, 4–22.Google Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.Google Scholar
Sadeghi, H., Lavoie, P. & Pollard, A. 2014 The effect of Reynolds number on the scaling range along the centreline of a round turbulent jet. J. Turbul. 15, 335–349.Google Scholar
Sadeghi, H., Lavoie, P. & Pollard, A. 2015 Equilibrium similarity solution of the turbulent transport equation along the centreline of a round jet. J. Fluid Mech. 772, 740–755.Google Scholar
Sadeghi, H., Lavoie, P. & Pollard, A. 2016 Scale-by-scale budget equation and its self-preservation in the shear layer of a free round jet. Intl J. Heat Fluid Flow 61, 85–95.Google Scholar
Sadeghi, H., Lavoie, P. & Pollard, A. 2018 Effects of finite hot-wire spatial resolution on turbulence statistics and velocity spectra in a round turbulent free jet. Exp. Fluids 59, 40.Google Scholar
Sadeghi, H. & Pollard, A. 2012 Effects of passive control rings positioned in the shear layer and potential core of a turbulent round jet. Phys. Fluids 24, 115103.Google Scholar
Talluru, K. M., Djenidi, L., Kamruzzaman, Md. & Antonia, R. A. 2016 Self-preservation in a zero pressure gradient rough-wall turbulent boundary layer. J. Fluid Mech. 788, 57–69.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent shear Flows, 1st edn. Cambridge University Press.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flows, 2nd edn. Cambridge University Press.Google Scholar
Vu, T. K., Gefferson, G. F. & Carminati, J. 2012 Finding higher symmetries of differential equations using the maple package desolvii. Comput. Phys. Commun. 183, 1044–1054.Google Scholar
Waclawczyk, M., Staffolani, N., Oberlack, M., Rosteck, A., Wilczek, M. & Friedrich, R. 2014 Statistical symmetries of the Lundgren–Monin–Novikov hierarchy. Phys. Rev. E 90, 013022.Google Scholar
Xu, G. & Antonia, R. A. 2002 Effect of different initial conditions on a turbulent round free jet. Exp. Fluids 33, 677–683.Google Scholar