Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-10T05:50:21.758Z Has data issue: false hasContentIssue false
  • English
  • Français

On mixing a density interface by a bubble plume

Published online by Cambridge University Press:  03 August 2016

Iran E. Lima Neto ,
Silvana S. S. Cardoso  and
Andrew W. Woods
Iran E. Lima Neto
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Chemical Engineering and Biotechnology, University of Cambridge, Pembroke Street, Cambridge CB2 3RA, UK
Silvana S. S. Cardoso
Affiliation:
Department of Chemical Engineering and Biotechnology, University of Cambridge, Pembroke Street, Cambridge CB2 3RA, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Chemical Engineering and Biotechnology, University of Cambridge, Pembroke Street, Cambridge CB2 3RA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe new experiments in which a bubble plume, produced from a point source of bubbles, rises through an ambient fluid composed of two layers of fluid of different density. In the lower layer, the speed of the plume exceeds the bubble rise speed and the motion is well described using classical theory of turbulent buoyant plumes. As the mixture enters the upper layer, it is either buoyant and rises to the top of the layer, or is negatively buoyant and forms a fountain. In our experiments, in which a fountain forms in the upper layer, the bubble rise speed exceeds the characteristic speed of this fountain, and a separated flow develops. The bubbles rise to the top of the system, while the lower layer fluid in the fountain rises a finite distance into the upper layer, entrains some of the upper layer fluid, and then collapses. This mixture of fluids then feeds a growing layer of density which is intermediate between the upper and lower layer. The height of rise of the fountain scales with the square of the Froude number of the fountain and the rate of entrainment of upper layer fluid into the fountain is directly proportional to the height of the fountain. 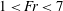This is analogous to the scaling for single-phase fountains with Froude numbers in the same range, $1<Fr<7$, but the constants of proportionality are smaller. We illustrate the relevance of the work for the design of mixing and aeration systems in freshwater reservoirs.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Gas/liquid flow Convection: Plumes/thermals
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , R3
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansong, J. K., Kyba, P. J. & Sutherland, B. R. 2008 Fountains impinging on a density interface. J. Fluid Mech. 595, 115–139.Google Scholar
Asaeda, T. & Imberger, J. 1993 Structure of bubble plumes in linearly stratified environments. J. Fluid Mech. 249, 35–57.Google Scholar
Baines, W., Corriveau, A. F. & Reedman, T. J. 1993 Turbulent fountains in a closed chamber. J. Fluid Mech. 255, 621–646.CrossRefGoogle Scholar
Baines, W. & Leitch, A. 1992 Destruction of stratification by a bubble plume. J. Hydraul. Engng 118 (4), 559–577.Google Scholar
Baines, W. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Baines, W. D. 1975 Entrainment by a jet or plume at a density interface. J. Fluid Mech. 68, 309–320.Google Scholar
Bloomfield, L. J. & Kerr, R. C. 1998 Turbulent fountains in a stratified fluid. J. Fluid Mech. 358, 335–356.Google Scholar
Camassa, R., Lin, Z., Mclaughlin, R. M., Mertins, K., Tzou, C., Walsh, J. & White, B. 2016 Optimal mixing of buoyant jets and plumes in stratified fluids: theory and experiments. J. Fluid Mech. 790, 790–805.CrossRefGoogle Scholar
Cardoso, S. S. S. & Woods, A. W. 1993 Mixing by a turbulent plume in a confined stratified region. J. Fluid Mech. 250, 277–305.Google Scholar
Chen, M. H. & Cardoso, S. S. S. 2000 The mixing of liquids by low Reynolds number plumes. Chem. Engng Sci. 55 (14), 2585–2594.Google Scholar
Clift, R., Grace, J. & Weber, M. E. 1978 Bubbles, Drops and Particles. pp. 1–693. Academic.Google Scholar
Friedman, P. & Katz, J. 2000 Rise height for negatively buoyant fountains and depth of penetration for negatively buoyant jets impinging an interface. Trans. ASME: J. Fluid. Engng 122, 779–782.Google Scholar
Hunt, G. & Burridge, H. 2015 Fountains in industry and nature. Annu. Rev. Fluid Mech. 47, 195–220.Google Scholar
Kim, S., Kim, J., Park, H. & Park, N. 2010 Effects of bubble size and diffusing area on destratification efficiency in bubble plumes of two layer stratification. J. Hydraul. Engng 136 (2), 106–115.Google Scholar
Kumagai, M. 1984 Turbulent buoyant convection from a source in a confined two layered region. J. Fluid Mech. 147, 105–131.Google Scholar
Lin, Y. & Linden, P. 2005 The entrainment due to a turbulent fountain at a density interface. J. Fluid Mech. 252, 25–52.Google Scholar
Mcdougall, T. J. 1978 Bubble plumes in stratified environments. J. Fluid Mech. 85, 655–672.CrossRefGoogle Scholar
McGinnis, D., Lorke, A., Wuest, A., Stockli, A. & Little, J. 2004 Interaction of a bubble plume and the near field in a stratified lake. Water Resour. Res. 40, W10206.CrossRefGoogle Scholar
Milgram, H. 1983 Mean flow in round bubble plumes. J. Fluid Mech. 133, 345–376.CrossRefGoogle Scholar
Morton, B., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection production by instantaneous and maintained point sources of buoyancy. Proc. R. Soc. Lond. A 231, 1–21.Google Scholar
Mott, R. & Woods, A. W. 2009 On the mixing in a confined stratified fluid by a turbulent buoyant plume. J. Fluid Mech. 623, 149–165.Google Scholar
Socolofsky, S. & Adams, E. 2003 Liquid volume fluxes in stratified multiphase plumes. J. Hydraul. Engng 129 (11), 905–914.Google Scholar
Socolofsky, S. & Adams, E. 2005 Role of slip velocity in the behaviour of stratified multiphase plumes. J. Hydraul. Engng 131 (4), 273–282.Google Scholar
Turner, J. S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26, 779–792.CrossRefGoogle Scholar
Wuest, A., Brooks, N. & Imboden, D. 1992 Bubble plume modelling for lake restoration. Water Resour. Res. 28, 3235–3250.Google Scholar