Published online by Cambridge University Press: 06 October 2015
The numerical simulation of gravity-driven flow of smooth inelastic hard disks through a channel, dubbed ‘granular’ Poiseuille flow, is conducted using event-driven techniques. We find that the variation of the mass-flow rate (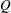 $Q$) with Knudsen number (
$Q$) with Knudsen number (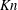 $Kn$) can be non-monotonic in the elastic limit (i.e. the restitution coefficient
$Kn$) can be non-monotonic in the elastic limit (i.e. the restitution coefficient 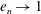 $e_{n}\rightarrow 1$) in channels with very smooth walls. The Knudsen-minimum effect (i.e. the minimum flow rate occurring at
$e_{n}\rightarrow 1$) in channels with very smooth walls. The Knudsen-minimum effect (i.e. the minimum flow rate occurring at 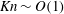 $Kn\sim O(1)$ for the Poiseuille flow of a molecular gas) is found to be absent in a granular gas with
$Kn\sim O(1)$ for the Poiseuille flow of a molecular gas) is found to be absent in a granular gas with 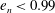 $e_{n}<0.99$, irrespective of the value of the wall roughness. Another rarefaction phenomenon, the bimodality of the temperature profile, with a local minimum (
$e_{n}<0.99$, irrespective of the value of the wall roughness. Another rarefaction phenomenon, the bimodality of the temperature profile, with a local minimum (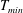 $T_{\mathit{min}}$) at the channel centerline and two symmetric maxima (
$T_{\mathit{min}}$) at the channel centerline and two symmetric maxima (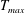 $T_{\mathit{max}}$) away from the centerline, is also studied. We show that the inelastic dissipation is responsible for the onset of temperature bimodality (i.e. the ‘excess’ temperature,
$T_{\mathit{max}}$) away from the centerline, is also studied. We show that the inelastic dissipation is responsible for the onset of temperature bimodality (i.e. the ‘excess’ temperature, 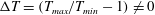 ${\rm\Delta}T=(T_{\mathit{max}}/T_{\mathit{min}}-1)\neq 0$) near the continuum limit (
${\rm\Delta}T=(T_{\mathit{max}}/T_{\mathit{min}}-1)\neq 0$) near the continuum limit (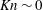 $Kn\sim 0$), but the rarefaction being its origin (as in the molecular gas) holds beyond
$Kn\sim 0$), but the rarefaction being its origin (as in the molecular gas) holds beyond 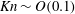 $Kn\sim O(0.1)$. The dependence of the excess temperature
$Kn\sim O(0.1)$. The dependence of the excess temperature 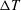 ${\rm\Delta}T$ on the restitution coefficient is compared with the predictions of a kinetic model, with reasonable agreement in the appropriate limit. The competition between dissipation and rarefaction seems to be responsible for the observed dependence of both the mass-flow rate and the temperature bimodality on
${\rm\Delta}T$ on the restitution coefficient is compared with the predictions of a kinetic model, with reasonable agreement in the appropriate limit. The competition between dissipation and rarefaction seems to be responsible for the observed dependence of both the mass-flow rate and the temperature bimodality on 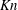 $Kn$ and
$Kn$ and 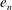 $e_{n}$ in this flow. The validity of the Navier–Stokes-order hydrodynamics for granular Poiseuille flow is discussed with reference to the prediction of bimodal temperature profiles and related surrogates.
$e_{n}$ in this flow. The validity of the Navier–Stokes-order hydrodynamics for granular Poiseuille flow is discussed with reference to the prediction of bimodal temperature profiles and related surrogates.