Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T14:34:48.407Z Has data issue: false hasContentIssue false
  • English
  • Français

On cumulative nonlinear acoustic waveform distortions from high-speed jets

Published online by Cambridge University Press:  19 May 2014

W. J. Baars ,
C. E. Tinney ,
M. S. Wochner  and
M. F. Hamilton
W. J. Baars*
Affiliation:
Department of Aerospace Engineering & Engineering Mechanics, University of Texas at Austin, Austin, TX 78712, USA
C. E. Tinney
Affiliation:
Department of Aerospace Engineering & Engineering Mechanics, University of Texas at Austin, Austin, TX 78712, USA
M. S. Wochner*
Affiliation:
Applied Research Laboratories, University of Texas at Austin, Austin, TX 78713, USA
M. F. Hamilton
Affiliation:
Applied Research Laboratories, University of Texas at Austin, Austin, TX 78713, USA
*
†Present address: The University of Melbourne, Parkville VIC 3010, Australia. Email address for correspondence: [email protected]
‡Present address: AdBm Technologies, Austin, TX 78702, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

A model is proposed for predicting the presence of cumulative nonlinear distortions in the acoustic waveforms produced by high-speed jet flows. The model relies on the conventional definition of the acoustic shock formation distance and employs an effective Gol’dberg number 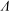$\Lambda $ for diverging acoustic waves. The latter properly accounts for spherical spreading, whereas the classical Gol’dberg number 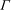$\Gamma $ is restricted to plane wave applications. Scaling laws are then derived to account for the effects imposed by jet exit conditions of practical interest and includes Mach number, temperature ratio, Strouhal number and an absolute observer distance relative to a broadband Gaussian source. Surveys of the acoustic pressure produced by a laboratory-scale, shock-free and unheated Mach 3 jet are used to support findings of the model. Acoustic waveforms are acquired on a two-dimensional grid extending out to 145 nozzle diameters from the jet exit plane. Various statistical metrics are employed to examine the degree of local and cumulative nonlinearity in the measured waveforms and their temporal derivatives. This includes a wave steepening factor (WSF), skewness, kurtosis and the normalized quadrature spectral density. The analysed data are shown to collapse reasonably well along rays emanating from the post-potential-core region of the jet. An application of the generalized Burgers equation is used to demonstrate the effect of cumulative nonlinear distortion on an arbitrary acoustic waveform produced by a high-convective-Mach-number supersonic jet. It is advocated that cumulative nonlinear distortion effects during far-field sound propagation are too subtle in this range-restricted environment and over the region covered, which may be true for other laboratory-scale jet noise facilities.

JFM classification

Acoustics: Acoustics Acoustics: Aeroacoustics Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 749 , 25 June 2014 , pp. 331 - 366
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baars, W. J.2013 Acoustics from high-speed jets with crackle. PhD thesis, The University of Texas at Austin, Austin, TX.Google Scholar
Baars, W. J. & Tinney, C. E. 2013 Transient wall pressures in an overexpanded and large area ratio nozzle. Exp. Fluids 54 (2), 1–17.CrossRefGoogle Scholar
Baars, W. J. & Tinney, C. E. 2014 Shock-structures in the acoustic field of a Mach 3 jet with crackle. J. Sound Vib. 333 (12), 2539–2553.CrossRefGoogle Scholar
Baars, W. J., Tinney, C. E., Murray, N. E., Jansen, B. J. & Panickar, P.2011 The effect of heat on turbulent mixing noise in supersonic jets. AIAA Paper 2011-1029.Google Scholar
Bendat, J. S. & Piersol, A. G. 1980 Engineering Applications of Correlation and Spectral Analysis. Wiley.Google Scholar
Blackstock, D. T. 2000 Fundamentals of Physical Acoustics. John Wiley & Sons.Google Scholar
Crighton, D. G. 1986 Nonlinear Acoustic Propagation of Broadband Noise (ed. Krothapalli, A.  & Smith, C. A.), pp. 411–454. Springer.Google Scholar
Crighton, D. G. & Bashforth, S. 1980 Nonlinear propagation of broadband jet noise. AIAA Paper 1980-1039.Google Scholar
Ffowcs Williams, J. E. 1963 The noise from turbulence convected at high speed. Phil. Trans. R. Soc. Lond. A 255, 469–503.Google Scholar
Ffowcs Williams, J. E. & Maidanik, G. 1965 The Mach wave field radiated by supersonic turbulent shear flows. J. Fluid Mech. 21, 641–657.Google Scholar
Ffowcs Williams, J. E., Simson, J. & Virchis, V. J. 1975 ‘Crackle’: an annoying component of jet noise. J. Fluid Mech. 71, 251–271.Google Scholar
Fiévet, R., Baars, W. J., Silva, D. & Tinney, C. E. 2013 High fidelity measurements in the far-field of a Mach 3 jet. Bull. Am. Phys. Soc. 58 (18), D24.00007.Google Scholar
Gallagher, J. A. & McLaughlin, D. K.1981 Experiments on the nonlinear characteristics of noise propagation from low and moderate Reynolds number supersonic jets. AIAA Paper 1981-2041.CrossRefGoogle Scholar
Gee, K. L.2005 Prediction of nonlinear jet noise propagation. PhD thesis, The Pennsylvania State University, State College, PA.Google Scholar
Gee, K. L., Downing, J. M., James, M. M., McKinley, R. C., McKinley, R. L., Neilsen, T. B. & Wall, A. T.2012 Nonlinear evolution of noise from a military jet aircraft during ground run-up. AIAA Paper 2012-2258.Google Scholar
Gee, K. L., Sparrow, V. W., James, M. M., Downing, J. M., Hobbs, C. M., Gabrielson, T. B. & Atchley, A. A. 2008 The role of nonlinear effects in the propagation of noise from high-power jet aircraft. J. Acoust. Soc. Am. 123 (6), 4082–4092.Google Scholar
Greska, B., Krothapalli, A., Horne, W. C. & Burnside, N.2008 A near-field study of high temperature supersonic jets. AIAA Paper 2008-3026.Google Scholar
Hall, J. W., Hall, A. M., Pinier, J. T. & Glauser, M. N. 2009 Cross-spectral analysis of the pressure in a Mach 0.85 turbulent jet. AIAA J. 47 (1), 54–59.CrossRefGoogle Scholar
Hamilton, M. F. 2013 Effective Gol’dberg number for diverging waves. J. Acoust. Soc. Am. 134, 4099.Google Scholar
Hamilton, M. F. & Blackstock, D. T.(Eds) 2008 Nonlinear Acoustics. Acoustical Society of America.Google Scholar
Hammerton, P. W. & Crighton, D. G. 1993 Overturning of nonlinear acoustic waves. Part 1. A general method. J. Fluid Mech. 252, 585–599.Google Scholar
Howell, G. P. & Morfey, C. L. 1987 Nonlinear propagation of broadband noise signals. J. Sound Vib. 114 (2), 189–201.Google Scholar
Kerhervé, F., Fitzpatrick, J. & Jordan, P. 2006 The frequency dependence of jet turbulence for noise source modelling. J. Sound Vib. 296, 209–225.CrossRefGoogle Scholar
Kuo, C. W., Veltin, J. & McLaughlin, D. K.2010 Effects of jet noise source distribution on acoustic far-field measurements. AIAA Paper 2010-474.Google Scholar
Kuo, C.-W., Veltin, J. & McLaughlin, D. K. 2012 Effects of jet noise source distribution on acoustic far-field measurements. Intl J. Aeroacoust. 11 (7–8), 885–915.CrossRefGoogle Scholar
Laufer, J., Schlinker, R. & Kaplan, R. E. 1976 Experiments on supersonic jet noise. AIAA J. 14 (4), 489–497.Google Scholar
Lighthill, M. J. 1954 On sound generated aerodynamically. II. turbulence as a source of sound. Proc. R. Soc. Lond. A 222 (1148), 1–32.Google Scholar
McInerny, S. A. 1996 Launch vehicle acoustics part 2: statistics of the time domain data. J. Aircraft 33 (3), 518–523.Google Scholar
McInerny, S. A. & Ölçmen, S. M. 2005 High-intensity rocket noise: Nonlinear propagation, atmospheric absorption, and characterization. J. Acoust. Soc. Am. 117 (2), 578–591.Google Scholar
McLaughlin, D. K., Bridges, J. E. & Kuo, C. W.2010 On the scaling of small, heat simulated jet noise measurements to moderate size exhaust jets. AIAA Paper 2010-3956.Google Scholar
McLaughlin, D. K., Morrison, G. L. & Troutt, T. R. 1975 Experiments on the instability waves in a supersonic jet and their acoustic radiation. J. Fluid Mech. 69, 73–95.Google Scholar
Morfey, C. L. & Howell, G. P. 1981 Nonlinear propagation of aircraft noise in the atmosphere. AIAA J. 19 (8), 986–992.CrossRefGoogle Scholar
Morris, P. J. 1977 Flow characteristics of the large scale wave-like structure of a supersonic round jet. J. Sound Vib. 53 (2), 223–244.Google Scholar
Nagamatsu, H. T. & Horvay, G. 1970 Supersonic jet noise. In 8th Aerospace Sciences Meeting, AIAA.Google Scholar
Naugol’nykh, K. A., Soluyan, S. I. & Khokhlov, R. V. 1963 Spherical waves of finite amplitude in a viscous thermally conducting medium. Sov. Phys. Acoust. 9 (1), 42–46.Google Scholar
Norum, T. D. & Seiner, J. M. 1982 Broadband shock noise from supersonic jets. AIAA J. 20 (5), 68–73.Google Scholar
Papamoschou, D. & Debiasi, M. 1999 Noise measurements in supersonic jets treated with the Mach wave elimination method. AIAA J. 37 (2), 154–160.CrossRefGoogle Scholar
Papamoschou, D., Morris, P. J. & McLaughlin, D. K. 2010 Beamformed flow-acoustic correlations in a supersonic jet. AIAA J. 48 (10), 2445–2453.Google Scholar
Pestorius, F. M. & Blackstock, D. T. 1974 Propagation of finite-amplitude noise. In Finite-Amplitude Wave Effects in Fluids, Proceedings of the 1973 Symposium, pp. 24–29. IPC Science and Technology Press.Google Scholar
Petitjean, B. P., Viswanathan, K. & McLaughlin, D. K. 2006 Acoustic pressure waveforms measured in high speed jet noise experiencing nonlinear propagation. Intl J. Aeroacoust. 5 (2), 193–215.CrossRefGoogle Scholar
Phillips, O. M. 1960 On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 9, 1–28.Google Scholar
Potter, R. C.1968 An investigation to locate the acoustic sources in a high speed jet exhaust stream. TR-68-4. Wyle Laboratories.Google Scholar
Potter, R. C. & Crocker, M. J.1966 Acoustic prediction methods for rocket engines, including the effects of clustered engines and deflected exhaust flow. Contractor Rep. 566. NASA.Google Scholar
Saxena, S., Morris, P. J. & Viswanathan, K. 2009 Algorithm for the nonlinear propagation of broadband jet noise. AIAA J. 47 (1), 186–194.Google Scholar
Seiner, J. M., Bhat, T. R. S. & Ponton, M. K. 1994 Mach wave emission from a high-temperature supersonic jet. AIAA J. 32 (12), 2345–2350.CrossRefGoogle Scholar
Tam, C. K. W. 1995 Supersonic jet noise. Annu. Rev. Fluid Mech. 27, 17–43.Google Scholar
Tam, C. K. W. 2009 Mach wave radiation from high-speed jets. AIAA J. 47 (10), 2440–2448.CrossRefGoogle Scholar
Tam, C. K. W. & Chen, P. 1994 Turbulent mixing noise from supersonic jets. AIAA J. 32 (9), 1774–1780.Google Scholar
Tam, C. K. W., Golebiowski, M. & Seiner, J. M.1996 On the two components of turbulent mixing noise from supersonic jets. AIAA Paper 1996-1716.Google Scholar
Tam, C. K. W. & Hu, F. Q. 1989 On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.Google Scholar
Tam, C. K. W., Viswanathan, K., Ahuja, K. K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–292.Google Scholar
Tanna, H. K. & Dean, P. D. 1975 The influence of temperature on shock-free supersonic jet noise. J. Sound Vib. 39 (4), 429–460.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. The MIT Press.Google Scholar
Tinney, C. E., Ukeiley, L. S. & Glauser, M. N. 2008 Low-dimensional characteristics of a transonic jet. Part 2. Estimate and far-field prediction. J. Fluid Mech. 615, 53–92.CrossRefGoogle Scholar
Troutt, T. R. & McLaughlin, D. K. 1982 Experiments on the flow and acoustic properties of a moderate-Reynolds-number supersonic jet. J. Fluid Mech. 116, 123–156.Google Scholar
Varnier, J. 2001 Experimental study and simulation of rocket engine freejet noise. AIAA J. 39 (10), 1851–1859.Google Scholar
Veltin, J., Day, B. J. & McLaughlin, D. K. 2011 Correlation of flowfield and acoustic field measurements in high-speed jets. AIAA J. 49 (1), 150–163.Google Scholar
Viswanathan, K. 2004 Aeroacoustics of hot jets. J. Fluid Mech. 516, 39–82.Google Scholar
Viswanathan, K. 2006 Instrumentation considerations for accurate jet noise measurements. AIAA J. 44 (6), 1137–1149.Google Scholar
Viswanathan, K. 2008 Does a model-scale nozzle emit the same jet noise as a jet engine? AIAA J. 46 (2), 336–355.Google Scholar
Webster, D. A. & Blackstock, D. T.1978 Experimental investigation of outdoor propagation of finite-amplitude noise. Contractor Rep. 2992. NASA.Google Scholar
Witze, P. O. 1974 Centerline velocity decay of compressible free jets. AIAA J. 12 (4), 417–418.Google Scholar