While studying the problem of predicting freak waves it was realized that it would be advantageous to introduce a simple measure for such extreme events. Although it is customary to characterize extremes in terms of wave height or its maximum it is argued in this paper that wave height is an ill-defined quantity in contrast to, for example, the envelope of a wave train. Also, the last measure has physical relevance, because the square of the envelope is the potential energy of the wave train. 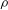The well-known representation of a narrow-band wave train is given in terms of a slowly varying envelope function ${\it\rho}$ and a slowly varying frequency 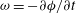${\it\omega}=-\partial {\it\phi}/\partial t$ where 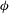${\it\phi}$ is the phase of the wave train. The key point is now that the notion of a local frequency and envelope is generalized by also applying the same definitions for a wave train with a broad-banded spectrum. It turns out that this reduction of a complicated signal to only two parameters, namely envelope and frequency, still provides useful information on how to characterize extreme events in a time series. As an example, for a linear wave train the joint probability distribution of envelope height and period is obtained and is validated against results from a Monte Carlo simulation. The extension to the nonlinear regime is, as will be seen, fairly straightforward.