Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zaripov, Dinar
Ivashchenko, Vladislav
Mullyadzhanov, Rustam
Li, Renfu
Markovich, Dmitriy
and
Kähler, Christian J.
2021.
Reverse flow phenomenon in duct corners at a low Reynolds number.
Physics of Fluids,
Vol. 33,
Issue. 8,
Ivashchenko, V A
Zaripov, D I
and
Mullyadzhanov, R I
2021.
The effect of Reynolds number on near-wall reverse flow in a turbulent duct flow.
Journal of Physics: Conference Series,
Vol. 2119,
Issue. 1,
p.
012032.
Agrawal, Rishav
Mishra, Debi Prasad
and
Poole, Robert J.
2022.
Numerical study of wall shear stress fluctuations and near-wall structures in a square duct at low Reynolds numbers.
Computers & Fluids,
Vol. 249,
Issue. ,
p.
105688.
Lopez-Doriga, Barbara
Dawson, Scott T.
and
Vinuesa, Ricardo
2022.
Resolvent analysis of laminar and turbulent rectangular duct flows.
Ivashchenko, V. A.
Lobanov, P. D.
Yavorsky, N. I.
Tokarev, M. P.
and
Mullyadzhanov, R. I.
2023.
Direct Numerical Simulation of the Peripheral and Internal Configurations of a Model Assembly of Fuel Elements.
Journal of Applied and Industrial Mathematics,
Vol. 17,
Issue. 2,
p.
320.
Reznik, A. L.
and
Soloviev, A. A.
2023.
Solving Fundamental and Applied Problems of Digital Image Processing at the Institute of Automation and Electrometry and Other Scientific Schools of the Siberian Branch of the Russian Academy of Sciences.
Pattern Recognition and Image Analysis,
Vol. 33,
Issue. 4,
p.
1260.
Gluzdov, D. S.
and
Gatapova, E. Ya.
2023.
Microchannel Surface Structures for Drag Reduction.
Journal of Engineering Thermophysics,
Vol. 32,
Issue. 2,
p.
214.
Zaripov, Dinar
Li, Renfu
Lukyanov, Alexey
Skrypnik, Artem
Ivashchenko, Elizaveta
Mullyadzhanov, Rustam
and
Markovich, Dmitriy
2023.
Backflow phenomenon in converging and diverging channels.
Experiments in Fluids,
Vol. 64,
Issue. 1,
Zaripov, D. I.
Ivashchenko, V. A.
Panteleev, S. A.
Luk’yanov, A. A.
and
Mullyadzhanov, R. I.
2023.
Direct Numerical Simulation of the Turbulent Flow Laminarization in a Pipe at Re = 5000.
Russian Aeronautics,
Vol. 66,
Issue. 4,
p.
723.
Chen, Xue
Chung, Yongmann M.
and
Wan, Minping
2023.
Backflow structures in turbulent pipe flows at low to moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Zaripov, D. I.
Lukyanov, A. A.
and
Markovich, D. M.
2023.
Experimental investigation of instantaneous local flow separation in a turbulent boundary layer at various Reynolds numbers.
Thermophysics and Aeromechanics,
Vol. 29,
Issue. 5,
p.
647.
Chuprov, I. V.
Ivashchenko, V. A.
Mullyadzhanov, R. I.
and
Zaripov, D. I.
2024.
EFFECT OF WALL HEATING ON THE CHARACTERISTICS OF NEAR-WALL REVERSE FLOW EVENTS OCCURRING IN A TURBULENT DUCT.
Journal of Applied Mechanics and Technical Physics,
Vol. 65,
Issue. 1,
p.
112.
Chen, Xue
Chung, Yongmann M.
and
Wan, Minping
2024.
The statistical characteristics and auto-regeneration of backflow in non-Newtonian turbulent pipe flow.
Physics of Fluids,
Vol. 36,
Issue. 2,
Chen, Xue
Chung, Yongmann M.
and
Wan, Minping
2025.
Proceedings of the Cambridge Unsteady Flow Symposium 2024.
p.
231.
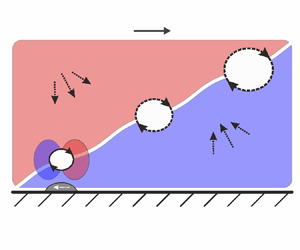
 $Re_\tau \simeq 200$. The analysis demonstrates the existence of a large-scale high-momentum flow structure originating upstream of a NWRF region. We propose a conceptual model of the NWRF formation and suggest that they are caused by intensive hairpin vortices incipient at the interface between large-scale high- and low-momentum flow regions identified using a conditional averaging procedure. The similarity of a flow topology associated with the NWRF region for
$Re_\tau \simeq 200$. The analysis demonstrates the existence of a large-scale high-momentum flow structure originating upstream of a NWRF region. We propose a conceptual model of the NWRF formation and suggest that they are caused by intensive hairpin vortices incipient at the interface between large-scale high- and low-momentum flow regions identified using a conditional averaging procedure. The similarity of a flow topology associated with the NWRF region for  $Re_\tau \simeq 200$ with those for
$Re_\tau \simeq 200$ with those for  $Re_\tau \simeq 1000$ (Chin et al., Phys. Rev. Fluids, vol. 3, issue 11, 2018, p. 114607) and
$Re_\tau \simeq 1000$ (Chin et al., Phys. Rev. Fluids, vol. 3, issue 11, 2018, p. 114607) and  $550 \leqslant Re_\tau \leqslant 2000$ (Cardesa et al., J. Fluid Mech., vol. 880, 2019) indicates the generality of the proposed mechanism.
$550 \leqslant Re_\tau \leqslant 2000$ (Cardesa et al., J. Fluid Mech., vol. 880, 2019) indicates the generality of the proposed mechanism.


