Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T13:19:14.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Off-plane motion of a prolate capsule in shear flow

Published online by Cambridge University Press:  13 March 2013

C. Dupont ,
A.-V. Salsac  and
D. Barthès-Biesel
C. Dupont
Affiliation:
Laboratoire de Biomécanique et Bioingénierie (UMR CNRS 7338), Université de Technologie de Compiègne, BP 20529, 60205 Compiègne, France Laboratoire de Mécanique des Solides (UMR CNRS 7649), Ecole Polytechnique, 91128 Palaiseau CEDEX, France
A.-V. Salsac*
Affiliation:
Laboratoire de Biomécanique et Bioingénierie (UMR CNRS 7338), Université de Technologie de Compiègne, BP 20529, 60205 Compiègne, France
D. Barthès-Biesel
Affiliation:
Laboratoire de Biomécanique et Bioingénierie (UMR CNRS 7338), Université de Technologie de Compiègne, BP 20529, 60205 Compiègne, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The objective of this study is to investigate the motion of an ellipsoidal capsule in a simple shear flow when its revolution axis is initially placed off the shear plane. We consider prolate capsules with an aspect ratio of two or three enclosed by a membrane, which is either strain-hardening or strain-softening. We seek the equilibrium motion of the capsule as we increase the capillary number 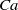$\mathit{Ca}$, which measures the ratio between the viscous and elastic forces. The three-dimensional fluid–structure interaction problem is solved numerically by coupling a boundary integral method (for the internal and external flows) with a finite element method (for the wall deformation). For any initial inclination with the flow vorticity axis, a given capsule converges towards a unique equilibrium configuration which depends on 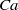$\mathit{Ca}$. At low capillary number, the stable equilibrium motion is the rolling regime: the capsule aligns its long axis with the vorticity axis, while the membrane tank-treads. As 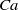$\mathit{Ca}$ increases, the capsule takes a complex wobbling motion at equilibrium, precessing around the vorticity axis. As 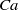$\mathit{Ca}$ is further increased, the capsule long axis oscillates about the shear plane, while the membrane rotates around a capsule cross-section that also oscillates over time (oscillating–swinging regime). The amplitude of the oscillations about the shear plane decreases as 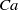$\mathit{Ca}$ increases and the capsule finally takes a swinging motion in the shear plane. It is found that the transitions from rolling to wobbling and from wobbling to oscillating–swinging depend on the mean energy stored in the membrane.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Capsule/cell dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 180 - 198
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abkarian, M., Faivre, M. & Viallat, A. 2007 Swinging of red blood cells under shear flow. Phys. Rev. Lett. 98, 188302.Google Scholar
Abkarian, M., Lartigue, C. & Viallat, A. 2001 Motion of phospholipidic vesicles along an inclined plane: sliding and rolling. Phys. Rev. E 63, 041906.Google Scholar
Abkarian, M. & Viallat, A. 2008 Vesicles and red blood cells in shear flow. Soft Matt. 4, 653–657.Google Scholar
Andry, M.-C., Edwards-Lévy, F. & Lévy, M.-C. 1996 Free amino group content of serum albumin microcapsules. III. A study at low pH values. Intl J. Pharmaceut. 128 (1), 197–202.CrossRefGoogle Scholar
Barthès-Biesel, D. 2011 Modelling the motion of capsules in flow. Curr. Opin. Colloid Interface Sci. 16, 3–12.Google Scholar
Barthès-Biesel, D., Diaz, A. & Dhenin, E. 2002 Effect of constitutive laws for two-dimensional membranes on flow-induced capsule deformation. J. Fluid Mech. 460, 211–222.Google Scholar
Barthès-Biesel, D. & Rallison, J. M. 1981 The time-dependent deformation of a capsule freely suspended in a linear shear flow. J. Fluid Mech. 113, 251–267.CrossRefGoogle Scholar
Barthès-Biesel, D., Walter, J. & Salsac, A.-V. 2010 Flow-induced deformation of artificial capsules. In Computational Hydrodynamics of Capsules and Biological Cells, pp. 35–70. Taylor & Francis.Google Scholar
Carin, M., Barthès-Biesel, D., Edwards-Lévy, F., Postel, C. & Andrei, D. C. 2003 Compression of biocompatible liquid-filled HSA-alginate capsules: determination of the membrane mechanical properties. Biotechnol. Bioengng 82 (2), 207–212.CrossRefGoogle ScholarPubMed
Chang, K. S. & Olbricht, W. L. 1993 Experimental studies of the deformation and breakup of a synthetic capsule in steady and unsteady simple shear flow. J. Fluid Mech. 250, 609–633.Google Scholar
Chang, T. M. S., Macintosh, F. C. & Mason, S. G. 1966 Semipermeable aqueous microcapsules: I. Preparation and properties. Can. J. Physiol. Pharmacol. 44, 115–128.Google Scholar
Chu, T. X., Salsac, A.-V., Leclerc, E., Barthès-Biesel, D., Wurtz, H. & Edwards-Lévy, F. 2011 Comparison between measurements of elasticity and free amino group content of ovalbumin microcapsule membranes: discrimination of the cross-linking degree. J. Colloid Interface Sci. 355 (1), 81–88.CrossRefGoogle ScholarPubMed
Dupire, J., Socol, M. & Viallat, A. 2012 Full dynamics of a red blood cell in shear flow. Proc. Natl Acad. Sci. U.S.A. 109 (51), 20808–20813.CrossRefGoogle ScholarPubMed
Edwards-Lévy, F., Andry, M.-C. & Lévy, M.-C. 1993 Determination of free amino group content of serum albumin microcapsules using trinitrobenzenesulfonic acid: effect of variations in polycondensation pH. Intl J. Pharmaceut. 96 (13), 85–90.Google Scholar
Edwards-Lévy, F., Andry, M.-C. & Lévy, M.-C. 1994 Determination of free amino group content of serum albumin microcapsules: II. Effect of variations in reaction time and in terephthaloyl chloride concentration. Intl J. Pharmaceut. 103 (3), 253–257.Google Scholar
Foessel, E., Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Influence of internal viscosity on the large deformation and buckling of a spherical capsule in a simple shear flow. J. Fluid Mech. 672, 477–486.Google Scholar
Hay, K. L. & Bull, B. S. 2009 Statistical clues to postoperative blood loss: Moving averages applied to medical data. Blood Cells Mol. Dis. 43 (3), 250–255.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. A 102, 161–179.Google Scholar
Koleva, I. & Rehage, H. 2012 Deformation and orientation dynamics of polysiloxane microcapsules in linear shear flow. Soft Matt. 8, 3681–3693.Google Scholar
Lac, E., Barthès-Biesel, D., Pelakasis, A. & Tsamopoulos, J. 2004 Spherical capsules in three-dimensional unbounded Stokes flows: effect of the membrane constitutive law and onset of buckling. J. Fluid Mech. 516, 303–334.Google Scholar
Lévy, M.-C., Andry, M.-C., Lefebvre, S. & Manfait, M. 1995 Fourier transform infrared spectroscopic studies of cross-linked human serum albumin microcapsules. 3. Influence of terephthaloyl chloride concentration on spectra and correlation with microcapsule morphology and size. J. Pharmaceut. Sci. 84 (2), 161–165.Google Scholar
Lévy, M.-C., Lefebvre, S., Andry, M.-C., Rahmouni, M. & Manfait, M. 1994 Fourier-transform infrared spectroscopic studies of cross-linked human serum albumin microcapsules. 2. Influence of reaction time on spectra and correlation with microcapsule morphology and size. J. Pharmaceut. Sci. 83 (3), 419–422.Google Scholar
Lévy, M.-C., Lefebvre, S., Rahmouni, M., Andry, M.-C. & Manfait, M. 1991 Fourier transform infrared spectroscopic studies of human serum albumin microcapsules prepared by interfacial cross-linking with terephthaloylchloride: influence of polycondensation pH on spectra and relation with microcapsule morphology and size. J. Pharmaceut. Sci. 80 (6), 578–585.Google Scholar
Li, X. & Sarkar, K. 2008 Front tracking simulation of deformation and buckling instability of a liquid capsule enclosed by an elastic membrane. J. Comput. Phys. 227, 4998–5018.Google Scholar
Liu, L., Yang, J.-P, Ju, X.-J., Xie, R., Yang, L., Liang, B. & Chu, L.-Y. 2009 Microfluidic preparation of monodisperse ethyl cellulose hollow microcapsules with non-toxic solvent. J. Colloid Interface Sci. 336 (1), 100–106.Google Scholar
Ramanujan, S. & Pozrikidis, C. 1998 Deformation of liquid capsules enclosed by elastic membranes in simple shear flow: large deformations and the effect of capsule viscosity. J. Fluid Mech. 361, 117–143.Google Scholar
Schneeweiss, I. & Rehage, H. 2005 Non-spherical capsules for the food industry. Chemie Ingenieur Technik 77 (3), 236–239.Google Scholar
Skalak, R., Tozeren, A., Zarda, R. P. & Chien, S. 1973 Strain energy function of red blood cell membranes. Biophys. J. 13, 245–264.Google Scholar
Sui, Y., Low, H. T., Chew, Y. T. & Roy, P. 2008 Tank-treading, swinging, and tumbling of liquid-filled elastic capsules in shear flow. Phys. Rev. E 77, 016310.Google Scholar
Walter, A., Rehage, H. & Leonhard, H. 2001 Shear induced deformation of microcapsules: shape oscillations and membrane folding. Colloids Surf. A: Physicochem Engng Aspects 183–185, 123–132.Google Scholar
Walter, J., Salsac, A.-V. & Barthès-Biesel, D. 2011 Ellipsoidal capsules in simple shear flow: prolate versus oblate initial shapes. J. Fluid Mech. 676, 318–347.Google Scholar
Walter, J., Salsac, A.-V., Barthès-Biesel, D. & Le Tallec, P. 2010 Coupling of finite element and boundary integral methods for a capsule in a Stokes flow. Intl J. Numer. Meth. Engng 83, 829–850.Google Scholar
Xiang, Z. Y., Lu, Y. C., Zou, Y., Gong, X. C. & Luo, G. S. 2008 Preparation of microcapsules containing ionic liquids with a new solvent extraction system. React. Funct. Polym. 68 (8), 1260–1265.Google Scholar
Zhang, L. & Salsac, A.-V. 2012 Can sonication enhance release from liquid-core capsules with a hydrogel membrane? J. Colloid Interface Sci. 368, 648–654.Google Scholar

Dupont et al. supplementary movie

Rolling motion of a prolate capsule with an aspect ratio of 2 and a strain-hardening Skalak membrane (C2SK). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 85°; the capillary number is Ca = 0.1. The points M and N are the membrane points initially located on the short and long axis respectively. Point P is at the tip of the long axis at time t.

Download Dupont et al. supplementary movie(Video)
Video 4.3 MB

Dupont et al. supplementary movie

Wobbling motion of a prolate capsule with an aspect ratio of 2 and a strain-hardening Skalak membrane (C2SK). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 15°; the capillary number is Ca = 0.9. The points M and N are the membrane points initially located on the short and long axis respectively. Point P is at the tip of the long axis at time t.

Download Dupont et al. supplementary movie(Video)
Video 1.4 MB

Dupont et al. supplementary movie

Oscillating-swinging of a prolate capsule with an aspect ratio of 2 and a strain-hardening Skalak membrane (C2SK). The initial inclination ζ0 of the revolution axis with the vorticity axis of the shear flow is 60°; the capillary number is Ca = 1.5. The points M and N are the membrane points initially located on the short and long axis respectively. Point P is at the tip of the long axis at time t.

Download Dupont et al. supplementary movie(Video)
Video 866.2 KB