Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T21:37:17.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Observations of gravity–capillary lump interactions

Published online by Cambridge University Press:  08 February 2017

Naeem Masnadi Open the ORCID record for Naeem Masnadi [Opens in a new window]  and
James H. Duncan Open the ORCID record for James H. Duncan [Opens in a new window]
Naeem Masnadi*
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
James H. Duncan
Affiliation:
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this experimental study, we investigate the interaction of gravity–capillary solitary waves generated by two surface pressure sources moving side by side at constant speed. The nonlinear response of a water surface to a single source moving at a speed just below the minimum phase speed of linear gravity–capillary waves in deep water (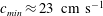$c_{min}\approx 23~\text{cm}~\text{s}^{-1}$) consists of periodic generation of pairs of three-dimensional solitary waves (or lumps) in a V-shaped pattern downstream of the source. In the reference frame of the laboratory, these unsteady lumps propagate in a direction oblique to the motion of the source. In the present experiments, the strengths of the two sources are adjusted to produce nearly identical responses and the free-surface deformations are visualized using photography-based techniques. The first lumps generated by the two sources move in intersecting directions that make a half-angle of approximately 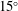$15^{\circ }$ and collide in the centreplane between the sources. A steep depression is formed during the collision, but this depression quickly decreases in amplitude while radiating small-amplitude radial waves. After the collision, a quasi-stable pattern is formed with several rows of localized depressions that are qualitatively similar to lumps but exhibit periodic amplitude oscillations, similar to a breather. The shape of the wave pattern and the period of oscillations depend strongly on the distance between the sources.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Waves/Free-surface Flows: Solitary waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 814 , 10 March 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akers, B. & Milewski, P. A. 2009 A model equation for wavepacket solitary waves arising from capillary–gravity flows. Stud. Appl. Maths 122 (3), 249–274.CrossRefGoogle Scholar
Akers, B. & Milewski, P. A. 2010 Dynamics of three-dimensional gravity–capillary solitary waves in deep water. SIAM J. Appl. Maths 70 (7), 2390–2408.Google Scholar
Chen, Y. & Yeh, H. 2014 Laboratory experiments on counter-propagating collisions of solitary waves. Part 1. Wave interactions. J. Fluid Mech. 749, 577–596.Google Scholar
Cho, Y., Diorio, J. D., Akylas, T. R. & Duncan, J. H. 2011 Resonantly forced gravity–capillary lumps on deep water. Part 2. Theoretical model. J. Fluid Mech. 672, 288–306.Google Scholar
Craig, W., Guyenne, P., Hammack, J., Henderson, D. & Sulem, C. 2006 Solitary water wave interactions. Phys. Fluids 18 (5), 057106.Google Scholar
Diorio, J., Cho, Y., Duncan, J. H. & Akylas, T. R. 2009 Gravity–capillary lumps generated by a moving pressure source. Phys. Rev. Lett. 103, 214502.Google Scholar
Diorio, J. D., Cho, Y., Duncan, J. H. & Akylas, T. R. 2011 Resonantly forced gravity–capillary lumps on deep water. Part 1. Experiments. J. Fluid Mech. 672, 268–287.Google Scholar
Kim, B. & Akylas, T. R. 2005 On gravity–capillary lumps. J. Fluid Mech. 540, 337–351.Google Scholar
Longuet-Higgins, M. S. 1989 Capillary–gravity waves of solitary type on deep water. J. Fluid Mech. 200, 451–470.Google Scholar
Masnadi, N.2016 Dynamics of nonlinear gravity–capillary waves in deep water near resonance. PhD thesis, University of Maryland College Park.Google Scholar
Masnadi, N. & Duncan, J. H. 2017 The generation of gravity–capillary solitary waves by a pressure source moving at a trans-critical speed. J. Fluid Mech. 810, 448–474.Google Scholar
Milewski, P. A. 2005 Three-dimensional localized solitary gravity–capillary waves. Commun. Math. Sci. 3 (1), 89–99.CrossRefGoogle Scholar
Milewski, P. A., Vanden-Broeck, J-M & Wang, Z. 2010 Dynamics of steep two-dimensional gravity–capillary solitary waves. J. Fluid Mech. 664, 466–477.Google Scholar
Părău, E. I. & Vanden-Broeck, J.-M. 2011 Three-dimensional waves beneath an ice sheet due to a steadily moving pressure. Phil. Trans. R. Soc. Lond. A 369 (1947), 2973–2988.Google Scholar
Părău, E. I., Vanden-Broeck, J.-M. & Cooker, M. J. 2005 Nonlinear three-dimensional gravity–capillary solitary waves. J. Fluid Mech. 536, 99–105.Google Scholar
Wang, Z. & Milewski, P. A. 2012 Dynamics of gravity–capillary solitary waves in deep water. J. Fluid Mech. 708, 480–501.CrossRefGoogle Scholar

Masnadi et al. supplementary movie

Refraction movie with 1 active air-jet located on the top-left of the images (corresponding to figure 2).

Download Masnadi et al. supplementary movie(Video)
Video 9.6 MB

Masnadi et al. supplementary movie

Refraction movie with 2 air-jets separated by 8 cm (corresponding to figure 3).

Download Masnadi et al. supplementary movie(Video)
Video 9.7 MB

Masnadi et al. supplementary movie

Refraction movie with 2 air-jets separated by 12 cm (corresponding to figure 4).

Download Masnadi et al. supplementary movie(Video)
Video 9.7 MB

Masnadi et al. supplementary movie

Refraction movies with 2 air-jets separated by 12 cm (reference frame of the lab, before the first collision)

Download Masnadi et al. supplementary movie(Video)
Video 4.4 MB

Masnadi et al. supplementary movie

Refraction movies with 2 air-jets separated by 12 cm (reference frame of the lab, before the first collision)

Download Masnadi et al. supplementary movie(Video)
Video 4.4 MB

Masnadi et al. supplementary movie

LIF movies in the center-plane of the tubes (corresponding to figures 9 and 10). From the top: one air jet tube active (light sheet 4 cm from air-jet), 2 air-jets with 4 cm separation, 2 air-jets with 8 cm separation, and 2 air-jets with 12 cm separation.

Download Masnadi et al. supplementary movie(Video)
Video 9 MB