Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T00:45:15.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Oblique internal-wave chain resonance over seabed corrugations

Published online by Cambridge University Press:  07 November 2017

Louis-Alexandre Couston Open the ORCID record for Louis-Alexandre Couston [Opens in a new window] ,
Yong Liang  and
Mohammad-Reza Alam Open the ORCID record for Mohammad-Reza Alam [Opens in a new window]
Louis-Alexandre Couston
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA CNRS, Aix Marseille Univ, Centrale Marseille, IRPHE, Marseille, France
Yong Liang
Affiliation:
Applied Science and Technology, University of California, Berkeley, CA 94720, USA
Mohammad-Reza Alam
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA Applied Science and Technology, University of California, Berkeley, CA 94720, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Here we show that monochromatic long-crested corrugations on an otherwise flat seafloor can coherently scatter the energy of an oblique incident internal wave to multiple multi-directional higher-mode internal waves via a series of resonant interactions. We demonstrate that a resonance between seabed corrugations and a normally or slightly oblique incident internal wave results in a series of follow-up resonant interactions, which take place between the same corrugations and successively resonated shorter waves. A chain resonance of internal waves that carries energy to small scales is thus obtained, and we find that the Richardson number decreases by several orders of magnitude over the corrugated patch. If the incidence angle is large, and the incident wave perfectly satisfies a resonance condition with the topography, it turns out that not many higher-mode resonance or near-resonance conditions can be satisfied, such that energy stays confined within the first few modes. Nevertheless, if the incident waves are sufficiently detuned from satisfying a perfect resonance condition with the seabed corrugations, then we show that this frequency detuning may balance off the large detuning due to oblique incidence, leading to a chain resonance that again carries energy to small scales. The evolution of the incident and resonated wave amplitudes is predicted from the envelope equation for internal waves over resonant seabed topography in a three-dimensional rotating fluid, which we derive considering the Boussinesq and 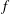$f$-plane approximations with 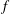$f$ the Coriolis frequency, linear density stratification and small-amplitude corrugations. Our results suggest that topographic features on the ocean floor with a well-defined dominant wavenumber vector, through the chain resonance mechanism elucidated here, may play a more important role than previously thought in the enhancement of diapycnal mixing and energy dissipation.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Topographic effects Waves/Free-surface Flows: Wave scattering
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 538 - 562
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M.-R. 2012 A new triad resonance between co-propagating surface and interfacial waves. J. Fluid Mech. 691, 267–278.CrossRefGoogle Scholar
Alam, M.-R., Liu, Y. & Yue, D. K. P. 2009 Bragg resonance of waves in a two-layer fluid propagating over bottom ripples. Part I. Perturbation analysis. J. Fluid Mech. 624, 191–224.CrossRefGoogle Scholar
Alam, M.-R. & Mei, C. C. 2007 Attenuation of long interfacial waves over a randomly rough seabed. J. Fluid Mech. 587, 73–96.CrossRefGoogle Scholar
Alford, M. H., MacKinnon, J. A., Zhao, Z., Pinkel, R., Klymak, J. & Peacock, T. 2007 Internal waves across the Pacific. Geophys. Res. Lett. 34 (24), 2–7.CrossRefGoogle Scholar
Alford, M. H. & Zhao, Z. 2007 Global patterns of low-mode internal-wave propagation. Part I: energy and energy flux. J. Phys. Oceanogr. 37, 1829–1848.CrossRefGoogle Scholar
Balmforth, N. J., Ierley, G. R. & Young, W. R. 2002 Tidal conversion by subcritical topography. J. Phys. Oceanogr. 32 (10), 2900–2914.2.0.CO;2>CrossRefGoogle Scholar
Becker, J. J., Sandwell, D. T., Smith, W. H. F., Braud, J., Binder, B., Depner, J., Fabre, D., Factor, J., Ingalls, S., Kim, S-H. et al. 2009 Global bathymetry and elevation data at 30 arc seconds resolution: SRTM30_PLUS. Mar. Geod. 32 (4), 355–371.CrossRefGoogle Scholar
Bell, T. H. 1975a Lee waves in stratified flows with simple harmonic time dependence. J. Fluid Mech. 67 (4), 705–722.CrossRefGoogle Scholar
Bell, T. H. 1975b Topographically generated internal waves in the open ocean. J. Geophys. Res. 80 (3), 320–327.CrossRefGoogle Scholar
Bühler, O. & Holmes-Cerfon, M. 2011 Decay of an internal tide due to random topography in the ocean. J. Fluid Mech. 678, 271–293.CrossRefGoogle Scholar
Bühler, O. & Muller, C. J. 2007 Instability and focusing of internal tides in the deep ocean. J. Fluid Mech. 588, 1–28.CrossRefGoogle Scholar
Chen, E.2009 Degradation of the internal tide over long bumpy topography. Woods Hole GFDL Annual Proceedings 2009, pp. 248–268.Google Scholar
Couston, L.-A., Jalali, M. A. & Alam, M.-R. 2017 Shore protection by oblique seabed bars. J. Fluid Mech. 815, 481–510.CrossRefGoogle Scholar
Elandt, R. B., Shakeri, M. & Alam, M.-R. 2014 Surface gravity-wave lensing. Phys. Rev. E 89, 1–6.CrossRefGoogle ScholarPubMed
Exarchou, E., Von Storch, J. S. & Jungclaus, J. H. 2012 Impact of tidal mixing with different scales of bottom roughness on the general circulation. Ocean Dyn. 62 (10–12), 1545–1563.CrossRefGoogle Scholar
Fredholm, I. 1903 Sur une classe d’équations fonctionnelles. Acta Mathematica 27 (1), 365–390.CrossRefGoogle Scholar
Galperin, B., Sukoriansky, S. & Anderson, P. S. 2007 On the critical Richardson number in stably stratified turbulence. Atmos. Sci. Lett. 8 (3), 65–69.CrossRefGoogle Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39 (1), 57–87.CrossRefGoogle Scholar
Goff, J. A. & Arbic, B. K. 2010 Global prediction of abyssal hill roughness statistics for use in ocean models from digital maps of paleo-spreading rate, paleo-ridge orientation, and sediment thickness. Ocean Model. 32, 36–43.CrossRefGoogle Scholar
Goff, J. A. & Jordan, T. H. 1988 Stochastic modeling of seafloor morphology: inversion of sea beam data for second-order statistics. J. Geophys. Res. 93 (B11), 13589.CrossRefGoogle Scholar
Guo, Y. & Holmes-Cerfon, M. 2016 Internal wave attractors over random, small-amplitude topography. J. Fluid Mech. 787, 148–174.CrossRefGoogle Scholar
Khatiwala, S. 2003 Generation of internal tides in an ocean of finite depth: analytical and numerical calculations. Deep-Sea Res. I 50, 3–21.CrossRefGoogle Scholar
Ledwell, J. R., Montgomery, E. T., Polzin, K. L., St Laurent, L. C., Schmitt, R. W. & Toole, J. M. 2000 Evidence for enhanced mixing over rough topography in the abyssal ocean. Nature 403, 179–182.CrossRefGoogle ScholarPubMed
Lefauve, A., Muller, C. & Melet, A. 2015 A three-dimensional map of tidal dissipation over abyssal hills. J. Geophys. Res. 120 (7), 4760–4777.CrossRefGoogle Scholar
Legg, S. 2014 Scattering of low-mode internal waves at finite isolated topography. J. Phys. Oceanogr. 44, 359–383.CrossRefGoogle Scholar
Li, Y. & Mei, C. C. 2014 Scattering of internal tides by irregular bathymetry of large extent. J. Fluid Mech. 747, 481–505.CrossRefGoogle Scholar
Liu, Y. & Yue, D. K. P. 1998 On generalized Bragg scattering of surface waves by bottom ripples. J. Fluid Mech. 356, 297–326.CrossRefGoogle Scholar
Llewellyn Smith, S. G. & Young, W. R. 2002 Conversion of the barotropic tide. J. Phys. Oceanogr. 32 (5), 1554–1566.2.0.CO;2>CrossRefGoogle Scholar
Mack, S. A. & Schoeberlein, H. C. 2004 Richardson number and ocean mixing: towed chain observations. J. Phys. Oceanogr. 34 (4), 736–754.2.0.CO;2>CrossRefGoogle Scholar
Mathur, M., Carter, G. S. & Peacock, T. 2014 Topographic scattering of the low-mode internal tide in the deep ocean. J. Geophys. Res. 119 (4), 2165–2182.CrossRefGoogle Scholar
Mei, C. C. 1985 Resonant reflection of surface water waves by periodic sandbars. J. Fluid Mech. 152, 315–335.CrossRefGoogle Scholar
Müller, P. & Xu, N. 1992 Scattering of oceanic internal gravity waves off random bottom topography. J. Phys. Oceanogr. 22 (5), 474–488.2.0.CO;2>CrossRefGoogle Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes II: energetics of tidal and wind mixing. Deep-Sea Res. I 45 (12), 1977–2010.CrossRefGoogle Scholar
Nash, J. D., Alford, M. H., Kunze, E., Martini, K. & Kelly, S. 2007 Hotspots of deep ocean mixing on the Oregon continental slope. Geophys. Res. Lett. 34 (L01605), 1–6.CrossRefGoogle Scholar
Nikurashin, M. & Ferrari, R. 2010 Radiation and dissipation of internal waves generated by geostrophic motions impinging on small-scale topography: application to the southern ocean. J. Phys. Oceanogr. 40 (9), 2025–2042.CrossRefGoogle Scholar
Polzin, K. L., Toole, J. M., Ledwell, J. R. & Schmitt, R. W. 1997 Spatial variability of turbulent mixing in the abyssal ocean. Science 276 (5309), 93–96.CrossRefGoogle ScholarPubMed
Sarkar, S. & Scotti, A. 2017 From topographic internal gravity waves to turbulence. Annu. Rev. Fluid Mech. 49, 195–220.CrossRefGoogle Scholar
Smith, W. H. F. & Sandwell, D. T. 1997 Global sea floor topography from satellite altimetry and ship depth soundings. Science 277 (5334), 1956–1962.CrossRefGoogle Scholar
St Laurent, L. & Garrett, C. 2002 The role of internal tides in mixing the deep ocean. J. Phys. Oceanogr. 32, 2882–2899.2.0.CO;2>CrossRefGoogle Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34, 559–593.CrossRefGoogle Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.CrossRefGoogle Scholar
Thurnherr, A. M., St Laurent, L. C., Speer, K. G., Toole, J. M. & Ledwell, J. R. 2005 Mixing associated with sills in a canyon on the midocean ridge flank. J. Phys. Oceanogr. 35, 1370–1381.CrossRefGoogle Scholar
Timko, P. G., Arbic, B. K., Goff, J. A., Ansong, J. K., Smith, W. H. F., Melet, A. & Wallcraft, A. J. 2017 Impact of synthetic abyssal hill roughness on resolved motions in numerical global ocean tide models. Ocean Model. 112, 1–16.CrossRefGoogle Scholar
Tobisch, E. 2016 New Approaches to Nonlinear Waves. Springer, Heidelberg, lecture no edn.CrossRefGoogle Scholar
Waterhouse, A. F., MacKinnon, J. A., Nash, J. D., Alford, M. H., Kunze, E., Simmons, H. L., Polzin, K. L., St Laurent, L. C., Sun, O. M., Pinkel, R. et al. 2014 Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate. J. Phys. Oceanogr. 44 (7), 1854–1872.CrossRefGoogle Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36 (1), 281–314.CrossRefGoogle Scholar
Yu, J. & Howard, L. N. 2012 Exact floquet theory for waves over arbitrary periodic topographies. J. Fluid Mech. 712, 1–20.CrossRefGoogle Scholar
Yu, J. & Mei, C. C. 2000a Do longshore bars shelter the shore? J. Fluid Mech. 404, 251–268.CrossRefGoogle Scholar
Yu, J. & Mei, C. C. 2000b Formation of sand bars under surface waves. J. Fluid Mech. 416, 315–348.CrossRefGoogle Scholar
Zhao, Z., Alford, M. H., Girton, J. B., Rainville, L. & Simmons, H. L. 2016 Global observations of open-ocean Mode-1 M2 internal tides. J. Phys. Oceanogr. 46 (6), 1657–1684.CrossRefGoogle Scholar
Zhao, Z., Alford, M. H., MacKinnon, J. A. & Pinkel, R. 2010 Long-range propagation of the semidiurnal internal tide from the hawaiian ridge. J. Phys. Oceanogr. 40, 713–736.CrossRefGoogle Scholar