Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T13:56:48.034Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study on unstable surfaces of oblique detonations

Published online by Cambridge University Press:  10 March 2014

Hong Hui Teng ,
Zong Lin Jiang  and
Hoi Dick Ng
Hong Hui Teng*
Affiliation:
State Key Lab of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing, 100190, China
Zong Lin Jiang
Affiliation:
State Key Lab of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing, 100190, China
Hoi Dick Ng
Affiliation:
Department of Mechanical and Industrial Engineering, Concordia University, Montreal, QC, Canada H3G 1M8
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, the onset of cellular structure on oblique detonation surfaces is investigated numerically using a one-step irreversible Arrhenius reaction kinetic model. Two types of oblique detonations are observed from the simulations. One is weakly unstable characterized by the existence of a planar surface, and the other is strongly unstable characterized by the immediate formation of the cellular structure. It is found that a high degree of overdrive suppresses the formation of cellular structures as confirmed by the results of many previous studies. 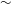However, the present investigation demonstrates that cellular structures also appear with degree of overdrive of 2.06 and 2.37, values much higher than ${\sim }$1.8 suggested previously in the literature for the critical value defining the instability boundary of oblique detonations. This contradiction could be explained by the use of differently shaped walls, a straight wall used in this study and a custom-designed curved wedge system so as to induce straight oblique detonations in previous studies. Another possible reason could be due to the low and possibly insufficient resolution used in previously published studies. Hence, simulations with different grid sizes are also performed to examine the effect of resolution on the numerical solutions. Using the present results, analysis also shows that although the characteristic lengths of unstable surfaces are different when the incident Mach number changes, these length scales are proportional to tangential velocities. Hence, the interior time determined by the overdrive degree is identified, and its limitation as the instability parameter is discussed.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Detonation waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 111 - 128
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourlioux, A. & Majda, A. J. 1992 Theoretical and numerical structure for unstable two-dimensional detonations. Combust. Flame 90, 211–229.Google Scholar
Bourlioux, A., Majda, A. J. & Roytburd, V. 1991 Theoretical and numerical structure for unstable one-dimensional detonations. SIAM J. Appl. Math. 51, 303–343.Google Scholar
Carpenter, M. H. & Casper, J. H. 1999 Accuracy of shock capturing in two spatial dimensions. AIAA J. 37, 1072–1079.Google Scholar
Choi, J. Y., Kim, D. W., Jeung, I. S., Ma, F. & Yang, V. 2007 Cell-like structure of unstable oblique detonation wave from high-resolution numerical simulation. Proc. Combust. Inst. 31, 2473–2480.Google Scholar
Choi, J. Y., Ma, F. H. & Yang, V. 2008 Some numerical issues on simulation of detonation cell structures. Combust. Explos. Shock Waves 44, 560–578.Google Scholar
Choi, J. Y., Shin, E. J. & Jeung, I. S. 2009 Unstable combustion induced by oblique shock waves at the non-attaching condition of the oblique detonation wave. Proc. Combust. Inst. 32, 2387–2396.CrossRefGoogle Scholar
Figueira da Silva, L. & Deshaies, B. 2000 Stabilization of an oblique detonation wave by a wedge: a parametric numerical study. Combust. Flame 121, 152–166.CrossRefGoogle Scholar
Fusina, G., Sislian, J. P. & Parent, B. 2005 Formation and stability of near chapman-jouguet standing oblique detonation waves. AIAA J. 43, 1591–1604.CrossRefGoogle Scholar
Grismer, M. J. & Powers, J. M. 1996 Numerical predictions of oblique detonation stability boundaries. Shock Waves 6, 147–156.Google Scholar
Gui, M. Y., Fan, B. C. & Dong, G. 2011 Periodic oscillation and fine structure of wedge-induced oblique detonation waves. Acta Mechanica Sin. 27, 922–928.Google Scholar
He, L. & Lee, J. H. S. 1995 The dynamical limit of one-dimensional detonation. Phys. Fluids 7, 1151–1158.CrossRefGoogle Scholar
Henrick, A. K., Aslam, T. D. & Powers, J. M. 2005 Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. J. Comput. Phys. 207, 542–567.Google Scholar
Henrick, A. K., Aslam, T. D. & Powers, J. M. 2006 Simulations of pulsating one-dimensional detonations with true fifth order accuracy. J. Comput. Phys. 213, 311–329.Google Scholar
Hwang, P., Fedkiw, R. P., Merriman, B., Aslam, T. D., Karagozian, A. R. & Osher, S. J. 1995 Numerical resolution of pulsating detonation waves. Combust. Theor. Model. 4, 217–240.Google Scholar
Kailasanath, K. 2003 Recent developments in the research on pulse detonation engines. AIAA J. 41, 154–159.Google Scholar
Lee, H. I. & Stewart, D. S. 1990 Calculation of linear detonation instability: one-dimensional instability of planar detonations. J. Fluid Mech. 216, 103–132.CrossRefGoogle Scholar
Li, C., Kailasanath, K. & Oran, E. S.1993 Effects of boundary layers on oblique-detonation structures AIAA Paper 1993-0450.CrossRefGoogle Scholar
Li, C., Kailasanath, K. & Oran, E. S. 1994 Detonation structures behind oblique shocks. Phys. Fluids 6, 1600–1611.Google Scholar
Mazaheri, K., Mahmoudi, Y. & Radulescu, M. I. 2012 Diffusion and hydrodynamic instabilities in gaseous detonations. Combust. Flame 159, 2138–2154.Google Scholar
Nettleton, M. A. 2000 The applications of unsteady, multi-dimensional studies of detonation waves to ram accelerators. Shock Waves 10, 9–22.Google Scholar
Ng, H. D. & Zhang, F. 2012 Detonation instability. In Shock Wave Science and Technology Reference Library (ed. Zhang, F.), vol. 6, pp. 107–212. Springer.Google Scholar
Papalexandris, M. V. 2000 Numerical study of wedge-induced detonations. Combust. Flame 120, 526–538.Google Scholar
Powers, J. M. 2006 Review of multiscale modeling of detonation. J. Propul. Power 22, 1217–1229.Google Scholar
Powers, J. M. & Aslam, T. D. 2006 Exact solution for multidimensional compressible reactive flow for verifying numerical algorithms. AIAA J. 44, 337–344.Google Scholar
et al. Quirk, J. J. 1994 Godunov-type schemes applied to detonation flows. In Combustion in High-Speed Flows (ed. Buckmaster, J.), pp. 575–596. Kluwer.Google Scholar
Rawat, P. S. & Zhong, X. 2010 On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions. J. Comput. Phys. 229, 6744–6780.Google Scholar
Romick, C. M., Aslam, T. D. & Powers, J. W. 2012 The effect of diffusion on the dynamics of unsteady detonations. J. Fluid Mech. 699, 453–464.Google Scholar
Roy, G. D., Frolov, S. M., Borisov, A. A. & Netzer, D. W. 2004 Pulse detonation propulsion: challenges, current status, and future perspective. Prog. Energy Combust. Sci. 30, 545–672.Google Scholar
Sharpe, G. J. 1997 Linear stability of idealized detonations. Proc. R. Soc. Lond. A 453, 2603–2625.CrossRefGoogle Scholar
Sharpe, G. J. & Falle, S. A. E. G. 1999 One-dimensional numerical simulations of idealized detonations. Proc. R. Soc. Lond. A 455, 1203–1214.Google Scholar
Sharpe, G. J. & Falle, S. A. E. G. 2000a Numerical simulations of pulsating detonations: I. Nonlinear stability of steady detonations. Combust. Theor. Model. 4, 557–574.Google Scholar
Sharpe, G. J. & Falle, S. A. E. G. 2000b Two-dimensional numerical simulations of idealized detonations. Proc. R. Soc. Lond. A 456, 2081–2100.CrossRefGoogle Scholar
Sharpe, G. J. & Quirk, J. J. 2008 Nonlinear cellular dynamics of the idealized detonation model: regular cells. Combust. Theor. Model. 12, 1–21.Google Scholar
Short, M. & Quirk, J. J. 1997 On the nonlinear stability and detonability limit of a detonation wave for a model three-step chain-branching reaction. J. Fluid Mech. 339, 89–119.CrossRefGoogle Scholar
Short, M. & Stewart, D. S. 1998 Cellular detonation instability. Part 1. A normal-mode linear analysis. J. Fluid Mech. 368, 229–262.Google Scholar
Taylor, B. D., Kasimov, A. R. & Stewart, D. S. 2009 Mode selection in weakly unstable two-dimensional detonations. Combust. Theor. Model. 13, 973–992.Google Scholar
Teng, H. H. & Jiang, Z. L. 2012 On the transition pattern of the oblique detonation structure. J. Fluid Mech. 713, 659–669.Google Scholar
Toro, E. F. 1999 Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer.Google Scholar
Verreault, J., Higgins, A. J. & Stowe, R. A. 2012 Formation and structure of steady oblique and conical detonation waves. AIAA J. 50, 1766–1772.Google Scholar
Verreault, J., Higgins, A. J. & Stowe, R. A. 2013 Formation of transverse waves in oblique detonations. Proc. Combust. Inst. 34, 1913–1920.Google Scholar
Viguier, C., Figueira da Silva, L., Desbordes, D. & Deshaies, B. 1997 Onset of oblique detonation waves: comparison between experimental and numerical results for hydrogen–air mixtures. Proc. Combust. Inst. 26, 3023–3031.CrossRefGoogle Scholar
Viguier, C., Gourara, A., Desbordes, D. & Deshaies, B. 1999 Three-dimensional structure of stabilization of oblique detonation wave in hypersonic flow. Proc. Combust. Inst. 26, 3023–3031.CrossRefGoogle Scholar
Vlasenko, V. V. & Sabelnikov, V. A. 1995 Numerical simulation of inviscid flows with hydrogen combustion behind shock waves and in detonation waves. Combust. Explos. Shock Waves 31, 376–389.Google Scholar
Yamaleev, N. K. & Carpenter, M. H. 2002 On accuracy of adaptive grid methods for captured shocks. J. Comput. Phys. 181, 280–316.Google Scholar