Published online by Cambridge University Press: 12 December 2014
Interaction between surface and interfacial waves with continuous energy spectra in a two-layer density stratified fluid system is investigated numerically. For an initial wave field which consists only of the surface waves all propagating in the same direction, it is confirmed that the spectra 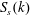 $S_{s}(k)$ of the surface waves and
$S_{s}(k)$ of the surface waves and 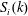 $S_{i}(k)$ of the interfacial waves change significantly due to the recently found class 3 triad resonance. When the bulk of the surface wave spectrum
$S_{i}(k)$ of the interfacial waves change significantly due to the recently found class 3 triad resonance. When the bulk of the surface wave spectrum 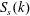 $S_{s}(k)$ is initially located well above the critical wavenumber
$S_{s}(k)$ is initially located well above the critical wavenumber 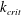 $k_{crit}$, below which the class 3 triad resonance is prohibited,
$k_{crit}$, below which the class 3 triad resonance is prohibited, 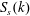 $S_{s}(k)$ downshifts gradually toward the lower wavenumber during the initial stage of evolution. However, this downshift halts when the peak of
$S_{s}(k)$ downshifts gradually toward the lower wavenumber during the initial stage of evolution. However, this downshift halts when the peak of 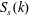 $S_{s}(k)$ reaches around
$S_{s}(k)$ reaches around 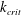 $k_{crit}$, and after that a steep peak forms in
$k_{crit}$, and after that a steep peak forms in 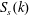 $S_{s}(k)$ around
$S_{s}(k)$ around 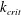 $k_{crit}$. It is confirmed that the timescale of the spectral evolution is of
$k_{crit}$. It is confirmed that the timescale of the spectral evolution is of 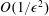 $O(1/{\it\epsilon}^{2})$ (
$O(1/{\it\epsilon}^{2})$ ( ${\it\epsilon}$ is a characteristic non-dimensional wave amplitude) in most of the
${\it\epsilon}$ is a characteristic non-dimensional wave amplitude) in most of the 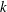 $k$ space, consistent with the prediction of the wave turbulence theory for a system with a decay-type dispersion relation. However, it is also found that the timescale of the formation and growth of the sharp peak in
$k$ space, consistent with the prediction of the wave turbulence theory for a system with a decay-type dispersion relation. However, it is also found that the timescale of the formation and growth of the sharp peak in 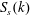 $S_{s}(k)$ around
$S_{s}(k)$ around 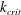 $k_{crit}$ is of
$k_{crit}$ is of 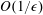 $O(1/{\it\epsilon})$, i.e. the timescale of the deterministic three-wave resonance.
$O(1/{\it\epsilon})$, i.e. the timescale of the deterministic three-wave resonance.