Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T07:22:04.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of wedge-induced oblique detonations in unsteady flow

Published online by Cambridge University Press:  01 August 2019

Pengfei Yang ,
Hoi Dick Ng  and
Honghui Teng Open the ORCID record for Honghui Teng [Opens in a new window]
Pengfei Yang
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, PR China State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, PR China
Hoi Dick Ng
Affiliation:
Department of Mechanical, Industrial and Aerospace Engineering, Concordia University, Montreal, QC, H3G 1M8, Canada
Honghui Teng*
Affiliation:
School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Oblique detonation waves (ODWs) have been studied widely to facilitate their employment in hypersonic propulsion, but the effects of continuous unsteady inflow have never been addressed so far. Thus, the present study investigates wedge-induced oblique detonations in unsteady flow via numerical simulations based on the reactive Euler equations with a two-step induction–reaction kinetic model. As a first step, the chemical and flow parameters are chosen for the simplest structure such that the ODW initiation occurs under a smooth transition with a curved shock. After a steady ODW with smooth initiation transition is established, the inflow is then subject to a continuous sinusoidal density/temperature disturbance. Cases with single-pulse inflow variation are also simulated to clarify whether the observed phenomena are derived solely from the continuous disturbance. Two aspects are analysed to investigate the features of ODWs in unsteady flow, namely, the formation of triple points on the surface, and the movement of the reactive front position. On the formation of triple points, the continuous disturbance generates at most one pair of triple points, less than or equal to the number of triple points in single-pulse cases. This indicates that the effects of continuous disturbance weaken the ability to generate the triple points, although there appear more triple points convected downstream on the surface at any given instant. On the movement of the reactive front, oscillatory behaviours are induced in either single-pulse or continuous disturbance cases. However, more complicated dynamic displacements and noticeable effects of unsteadiness are observed in the cases of continuous disturbance, and are found to be sensitive to the disturbance wavenumber, 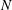$N$. Increasing 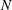$N$ results in three regimes with distinct behaviours, which are quasi-steady, overshooting oscillation and unstable ODW. For the quasi-steady case with low $N$, the reactive front oscillates coherently with the inflow disturbance with slightly higher amplitude around the initiation region. The overshooting oscillation generates the most significant variation of downstream surface in the case of modest 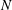$N$, reflecting a resonance-like behaviour of unsteady ODW. In the case of high 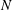$N$, the disturbed ODW surface readjusts itself with local unstable features. It becomes more robust and the reactive front of the final unstable ODW structure is less susceptible to flow disturbance.

JFM classification

Reacting Flows: Detonations
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 264 - 287
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashford, S. A. & Emanuel, G. 1994 Wave angle for oblique detonation waves. Shock Waves 3, 327–329.Google Scholar
Choi, J. Y., Kim, D. W., Jeung, I. S., Ma, F. & Yang, V. 2007 Cell-like structure of unstable oblique detonation wave from high-resolution numerical simulation. Proc. Combust. Inst. 31, 2473–2480.Google Scholar
Choi, J. Y., Shin, E. J. R. & Jeung, I. S. 2009 Unstable combustion induced by oblique shock waves at the non-attaching condition of the oblique detonation wave. Proc. Combust. Inst. 32, 2387–2396.Google Scholar
Emanuel, G. & Tuckness, D. G. 2004 Steady, oblique, detonation waves. Shock Waves 13, 445–451.Google Scholar
Fang, Y., Hu, Z. & Teng, H. 2018 Numerical investigation of oblique detonations induced by a finite wedge in a stoichiometric hydrogen-air mixture. Fuel 234, 502–507.Google Scholar
Fang, Y., Hu, Z., Teng, H., Jiang, Z. & Ng, H. D. 2017 Numerical study of inflow equivalence ratio inhomogeneity on oblique detonation formation in hydrogen-air mixtures. Aerosp. Sci. Technol. 24, 256–263.Google Scholar
Fickett, W. 1985 Introduction to Detonation Theory. University of California Press.Google Scholar
Fusina, G., Sislian, J. P. & Parent, B. 2005 Formation and stability of near Chapman–Jouguet standing oblique detonation waves. AIAA J. 43, 1591–1604.Google Scholar
Gamezo, V. N., Desbordes, D. & Oran, E. S. 1999 Formation and evolution of two-dimensional cellular detonations. Combust. Flame 116, 154–165.Google Scholar
Grismer, M. J. & Powers, J. M. 1996 Numerical predictions of oblique detonation stability boundaries. Shock Waves 6, 147–156.Google Scholar
Gross, R. A. 1963 Oblique detonation waves. AIAA J. 1, 1225–1227.Google Scholar
Gui, M. Y., Fan, B. C. & Dong, G. 2011 Periodic oscillation and fine structure of wedge induced oblique detonation waves. Acta Mechanica Sin. 6, 922–928.Google Scholar
Iwata, K., Nakaya, S. & Tsue, M. 2016 Numerical investigation of the effects of nonuniform premixing on shock-induced combustion. AIAA J. 54, 1682–1692.Google Scholar
Iwata, K., Nakaya, S. & Tsue, M. 2017 Wedge-stabilized oblique detonation in an inhomogeneous hydrogen–air mixture. Proc. Combust. Inst. 36, 2761–2769.Google Scholar
Jiang, Z. L. 2004 On dispersion-controlled principles for non-oscillatory shock-capturing schemes. Acta Mechanica Sin. 20, 1–15.Google Scholar
Ju, Y., Masuya, G. & Sasoh, A. 1998 Numerical and theoretical studies on detonation initiation by a supersonic projectile. Symp. (Int.) Combust 27, 2225–2231.Google Scholar
Kailasanath, K. 2003 Recent developments in the research on pulse detonation engines. AIAA J. 41, 145–159.Google Scholar
Lee, J. H. S. 2008 The Detonation Phenomenon, 2nd edn. Cambridge University Press.Google Scholar
Li, C., Kailasanath, K. & Oran, E. S. 1994 Detonation structures behind oblique shocks. Phys. Fluids 6, 1600–1611.Google Scholar
Liu, Y., Liu, Y. S., Wu, D. & Wang, J. P. 2016 Structure of an oblique detonation wave induced by a wedge. Shock Waves 26, 161–168.Google Scholar
Liu, Y., Wang, L., Xiao, B., Yan, Z. & Wang, C. 2018 Hysteresis phenomenon of the oblique detonation wave. Combust. Flame 192, 170–179.Google Scholar
Liu, Y., Wu, D., Yao, S. & Wang, J. P. 2015 Analytical and numerical investigations of wedge-induced oblique detonation waves at low inflow Mach number. Combust. Sci. Technol. 187, 843–856.Google Scholar
Maeda, S., Kasahara, J. & Matsuo, A. 2012 Oblique detonation wave stability around a spherical projectile by a high time resolution optical observation. Combust. Flame 159, 887–896.Google Scholar
Maeda, S., Sumiya, S., Kasahara, J. & Matsuo, A. 2013 Initiation and sustaining mechanisms of stabilized oblique detonation waves around projectiles. Proc. Combust. Inst. 34, 1973–1980.Google Scholar
Ng, H. D., Radulescu, M. I., Higgins, A. J., Nikiforakis, N. & Lee, J. H. S. 2005 Numerical investigation of the instability for one-dimensional Chapman–Jouguet detonations with chain-branching kinetics. Combust. Theor. Model. 9, 385–401.Google Scholar
Papalexandris, M. V. 2000 A numerical study of wedge-induced detonations. Combust. Flame 120, 526–538.Google Scholar
Pratt, D. T., Humphrey, J. W. & Glenn, D. E. 1991 Morphology of standing oblique detonation waves. J. Propul. Power 7, 837–845.Google Scholar
Qin, Q. & Zhang, X. 2018 A novel method for trigger location control of the oblique detonation wave by a modified wedge. Combust. Flame 197, 65–77.Google Scholar
Teng, H., Ng, H. D. & Jiang, Z. 2017 Initiation characteristics of wedge-induced oblique detonation waves in a stoichiometric hydrogen-air mixture. Proc. Combust. Inst. 36, 2735–2742.Google Scholar
Teng, H., Ng, H. D., Li, K., Luo, C. & Jiang, Z. 2015 Evolution of cellular structures on oblique detonation surfaces. Combust. Flame 162, 470–477.Google Scholar
Teng, H. H. & Jiang, Z. L. 2012 On the transition pattern of the oblique detonation structure. J. Fluid Mech. 713, 659–669.Google Scholar
Teng, H. H., Jiang, Z. L. & Ng, H. D. 2014 Numerical study on unstable surfaces of oblique detonations. J. Fluid Mech. 744, 111–128.Google Scholar
Teng, H. H., Zhao, W. & Jiang, Z. L. 2007 A novel oblique detonation structure and its stability. Chin. Phys. Lett. 24, 1985–1988.Google Scholar
Verreault, J., Higgins, A. J. & Stowe, R. A. 2013 Formation of transverse waves in oblique detonations. Proc. Combust. Inst. 34, 1913–1920.Google Scholar
Viguier, C., Gourara, A. & Desbordes, D. 1998 Three-dimensional structure of stabilization of oblique detonation wave in hypersonic flow. Symp. (Int.) Combust. 27, 2207–2214.Google Scholar
Wolanski, P. 2013 Detonative propulsion. Proc. Combust. Inst. 34, 125–158.Google Scholar
Yang, P., Teng, H., Jiang, Z. & Ng, H. D. 2018 Effects of inflow Mach number on oblique detonation initiation with a two-step induction-reaction kinetic model. Combust. Flame 193, 246–256.Google Scholar
Yang, P., Teng, H., Ng, H. D. & Jiang, Z. 2019 A numerical study on the instability of oblique detonation waves with a two-step inductionreaction kinetic model. Proc. Combust. Inst. 37, 3537–3544.Google Scholar
Zhang, Y., Yang, P., Teng, H., Ng, H. D. & Wen, C. 2018 Transition between different initiation structures of wedge-induced oblique detonations. AIAA J. 56, 4016–4023.Google Scholar