Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T11:45:16.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects

Published online by Cambridge University Press:  20 February 2015

Bo Wang ,
Neil D. Sandham ,
Zhiwei Hu  and
Weidong Liu
Bo Wang
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK College of Aerospace Science and Engineering, National University of Defence Technology, Changsha 410073, China
Neil D. Sandham*
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Zhiwei Hu
Affiliation:
Faculty of Engineering and the Environment, University of Southampton, Southampton SO17 1BJ, UK
Weidong Liu
Affiliation:
College of Aerospace Science and Engineering, National University of Defence Technology, Changsha 410073, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Large-eddy simulations are conducted to uncover physical aspects of sidewall-induced three-dimensionality for a moderately separated oblique shock-wave/boundary-layer interaction (SWBLI) at 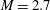$M=2.7$. Simulations are run for three different aspect ratios of the interaction zone. The swept SWBLI on the sidewalls and the corner flow behaviour are investigated, along with the main oblique SWBLI on the bottom wall. As the aspect ratio decreases to unity, the separation and reattachment points on the central plane are observed to move upstream simultaneously, while the bubble length initially increases and then stabilizes to a length 30 % larger than for the infinite-span quasi-two-dimensional case. A distorted incident shock and a three-dimensional (3D) bottom-wall separation pattern are observed, with a patch of attached flow between the central and corner separations. The 3D flow structure is found to be induced by the swept SWBLI formed on the sidewalls. The location of the termination point of the incident shock near the sidewall is limited by a sweepback effect, allowing the definition of a penetration Mach number 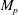$M_{p}$ that is shown to correlate well with the spanwise extent of the core flow. The structure and strength of the incident shock are modified significantly by the swept SWBLI on the sidewalls, along with a compression wave upstream and a secondary sidewall shock downstream, leading to a highly 3D pressure field in the main flow above the main SWBLI on the bottom wall. The reflection of the swept SWBLI from the bottom wall leads to a corner compression wave and strong transverse flow close to the bottom wall. A physical model based on the quasi-conical structure of the swept SWBLI on the sidewall is proposed to estimate the 3D SWBLI pattern on the bottom wall, in which the swept SWBLI features and the aspect ratio of the interaction zone are considered to be the critical factors.

JFM classification

Boundary Layers: Boundary layer separation Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 526 - 561
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvi, F. S. & Settles, G. S. 1992 Physical model of the swept shock wave/boundary-layer interaction flowfield. AIAA J. 30, 2252–2258.Google Scholar
Babinsky, H., Makinson, N. J. & Morgan, C. E.2007 Micro-vortex generator flow control for supersonic engine inlets. AIAA Paper 2007-521.Google Scholar
Babinsky, H. & Ogawa, H. 2008 SBLI control for wings and inlets. Shock Waves 18, 89–96.CrossRefGoogle Scholar
Babinsky, H., Oorebeek, J. & Cottingham, T. G.2013 Corner effects in reflecting oblique shock-wave/boundary-layer interactions. AIAA Paper 2013-0859.Google Scholar
Bookey, P., Wyckham, C. & Smits, A.2005 Experimental investigations of Mach 3 shock-wave turbulent boundary layer interactions. AIAA Paper 2005-4899.CrossRefGoogle Scholar
Bruce, P. J. K. & Babinsky, H.2009 Behaviour of unsteady transonic shock/boundary layer interactions with three-dimensional effects. AIAA Paper 2009-1590.CrossRefGoogle Scholar
Bruce, P. J. K., Burton, D. M. F., Titchener, N. T. & Babinsky, H. 2011 Corner effect and separation in transonic channel flows. J. Fluid Mech. 679, 247–262.Google Scholar
Burton, D. M. F. & Babinsky, H. 2012 Corner separation effects for normal shock wave/turbulent boundary layer interactions in rectangular channels. J. Fluid Mech. 707, 287–306.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction reserach: what next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Duan, L., Beekman, I. & Martin, M. P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 672, 245–267.Google Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 152, 517–549.Google Scholar
Dupont, P., Haddad, C. & Debieve, J. F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.CrossRefGoogle Scholar
Dussauge, J.-P. 2010 Basic experiments. In Unsteady Effects of Shock Wave Induced Separation (ed. Doerffer, P., Hirsch, C., Dussauge, J.-P., Babinsky, H. & Barakos, G. N.), pp. 315–320. Springer.Google Scholar
Dussauge, J.-P., Dupont, P. & Debieve, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10, 85–91.Google Scholar
Dussauge, J.-P. & Piponniau, S. 2008 Shock/boundary-layer interactions: possible sources of unsteadiness. J. Fluids Struct. 24, 1166–1175.Google Scholar
Eagle, W. E.2012 An experimental study of three-dimensional inlet shock-boundary layer interactions. PhD thesis, University of Michigan.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.Google Scholar
Garnier, E. 2009 Stimulated detached eddy simulation of three-dimensional shock/boundary layer interaction. Shock Waves 19, 479–486.CrossRefGoogle Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/boundary layer interaction. J. Fluid Mech. 622, 33–62.CrossRefGoogle Scholar
Inagaki, M., Kondoh, T. & Nagano, Y. 2005 A mixed-time-scale SGS model with fixed model-parameters for practical LES. Trans. ASME J. Fluids Engng 127, 1–13.CrossRefGoogle Scholar
Knight, D., Yan, H., Panaras, A. G. & Zheltovodov, A. 2003 Advances in CFD prediction of shockwave turbulent boundary layer interactions. Prog. Aerosp. Sci. 39, 121–184.Google Scholar
Lu, F. K. 1993 Quasiconical free interaction between a swept shock and a turbulent boundary layer. AIAA J. 31, 686–692.Google Scholar
Lund, T. S. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.CrossRefGoogle Scholar
Panaras, A. G. 1997 The effect of the structure of swept-shock-wave/turbulent-boundary-layer interactions on turbulence modelling. J. Fluid Mech. 338, 203–230.CrossRefGoogle Scholar
Piponniau, S., Dussauge, J. P., Debieve, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.Google Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at $M=2.25$ . Phys. Fluids 18, 065113.CrossRefGoogle Scholar
Priebe, S. & Martin, M. P. 2012 Low-frequency unsteadiness in shock wave–turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Reda, D. C. & Murphy, J. D. 1973 Shock wave/turbulent boundary-layer interactions in rectangular channels. AIAA J. 11 (2), 139–140.Google Scholar
Sandham, N. D., Li, Q. & Yee, H. C. 2002 Entropy splitting for high-order numerical simulation of compressible turbulence. J. Comput. Phys. 178, 307–322.Google Scholar
Sandhu, H. S. & Sandham, N. D.1994 Boundary conditions for spatially growing compressible shear layers. Tech. Rep. QMW-EP-1100.Google Scholar
Schlatter, P. & Orlu, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Touber, E.2010 Unsteadiness in shock wave boundary layer interactions. PhD thesis, University of Southampton.Google Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. J. Theor. Comput. Fluid Dyn. 23, 79–107.Google Scholar
Touber, E. & Sandham, N. D. 2011 Low-order stochastic modelling of low-frequency motions in reflected shock-wave/boundary-layer interactions. J. Fluid Mech. 671, 417–465.Google Scholar
Wang, B., Liu, W., Zhao, Y., Fan, X. & Wang, C. 2012 Experimental investigation of the micro-ramp based shock wave and turbulent boundary layer interaction control. Phys. Fluids 24, 055110.Google Scholar
White, F. M. 2006 Viscous Fluid Flow, 3rd edn. McGraw-Hill.Google Scholar
Wu, M. & Martin, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar
Xie, Z. T. & Castro, I. P. 2008 Efficient generation of inflow conditions for large-eddy simulation of street-scale flows. Flow Turbul. Combust. 81, 449–470.Google Scholar
Yee, H. C., Sandham, N. D. & Djomehri, M. J. 1999 Low-dissipative high order shock-capturing methods using characteristic-based filters. J. Comput. Phys. 150, 199–238.Google Scholar