Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-09T18:55:34.278Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical simulation of turbulent channel flow over a viscous hyper-elastic wall

Published online by Cambridge University Press:  05 October 2017

Marco E. Rosti Open the ORCID record for Marco E. Rosti [Opens in a new window]  and
Luca Brandt
Marco E. Rosti*
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
Luca Brandt
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform numerical simulations of a turbulent channel flow over an hyper-elastic wall. In the fluid region the flow is governed by the incompressible Navier–Stokes (NS) equations, while the solid is a neo-Hookean material satisfying the incompressible Mooney–Rivlin law. The multiphase flow is solved with a one-continuum formulation, using a monolithic velocity field for both the fluid and solid phase, which allows the use of a fully Eulerian formulation. 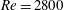The simulations are carried out at Reynolds bulk $Re=2800$ and examine the effect of different elasticity and viscosity of the deformable wall. We show that the skin friction increases monotonically with the material elastic modulus. The turbulent flow in the channel is affected by the moving wall even at low values of elasticity since non-zero fluctuations of vertical velocity at the interface influence the flow dynamics. The near-wall streaks and the associated quasi-streamwise vortices are strongly reduced near a highly elastic wall while the flow becomes more correlated in the spanwise direction, similarly to what happens for flows over rough and porous walls. As a consequence, the mean velocity profile in wall units is shifted downwards when shown in logarithmic scale, and the slope of the inertial range increases in comparison to that for the flow over a rigid wall. We propose a correlation between the downward shift of the inertial range, its slope and the wall-normal velocity fluctuations at the wall, extending results for the flow over rough walls. We finally show that the interface deformation is determined by the fluid fluctuations when the viscosity of the elastic layer is low, while when this is high the deformation is limited by the solid properties.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 830 , 10 November 2017 , pp. 708 - 735
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Krogstad, P. A. 2001 Turbulence structure in boundary layers over different types of surface roughness. Fluid Dyn. Res. 28 (2), 139–157.Google Scholar
Beavers, G. S., Sparrow, E. M. & Magnuson, R. A. 1970 Experiments on coupled parallel flows in a channel and a bounding porous medium. Trans. ASME J. Basic Engng 92, 843–848.Google Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.Google Scholar
Benjamin, T. B. 1960 Effects of a flexible boundary on hydrodynamic stability. J. Fluid Mech. 9 (04), 513–532.CrossRefGoogle Scholar
Bonet, J. & Wood, R. D. 1997 Nonlinear Continuum Mechanics for Finite Element Analysis. Cambridge University Press.Google Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.Google Scholar
Bushnell, D. M., Hefner, J. N. & Ash, R. L. 1977 Effect of compliant wall motion on turbulent boundary layers. Phys. Fluids A 20 (10), S31–S48.CrossRefGoogle Scholar
Cabal, A., Szumbarski, J. & Floryan, J. M. 2002 Stability of flow in a wavy channel. J. Fluid Mech. 457, 191–212.Google Scholar
Carpenter, P. W. & Garrad, A. D. 1985 The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1. Tollmien–Schlichting instabilities. J. Fluid Mech. 155, 465–510.CrossRefGoogle Scholar
Carpenter, P. W. & Morris, P. J. 1990 The effect of anisotropic wall compliance on boundary-layer stability and transition. J. Fluid Mech. 218, 171–223.Google Scholar
Chang, Y. C., Hou, T. Y., Merriman, B. & Osher, S. 1996 A level set formulation of eulerian interface capturing methods for incompressible fluid flows. J. Comput. Phys. 124 (2), 449–464.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary-Layer Meteorol. 104 (2), 229–259.Google Scholar
Choi, K. S., Yang, X., Clayton, B. R., Glover, E. J., Atlar, M., Semenov, B. N. & Kulik, V. M. 1997 Turbulent drag reduction using compliant surfaces. Proc. R. Soc. Lond. A 453, 2229–2240.Google Scholar
Clauser, F. H. 1954 Turbulent boundary layers in adverse pressure gradients. J. Aero. Sci. 21, 91–109.Google Scholar
Daniel, A. P., Gaster, M. & Willis, G. J. K.1987 Boundary layer stability on compliant surfaces. Tech. Rep. 35020. British Maritime Technology Ltd.Google Scholar
Davies, C. & Carpenter, P. W. 1997 Numerical simulation of the evolution of Tollmien–Schlichting waves over finite compliant panels. J. Fluid Mech. 335, 361–392.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Flores, O. & Jimenez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.Google Scholar
Gad-el Hak, M. 1986 The response of elastic and viscoelastic surfaces to a turbulent boundary layer. Trans. ASME J. Appl. Mech. 53 (1), 206–212.Google Scholar
Gad-el Hak, M. 1987 Compliant coatings research: a guide to the experimentalist. J. Fluids Struct. 1 (1), 55–70.Google Scholar
Gad-el Hak, M. 1996 Compliant coatings: a decade of progress. Appl. Mech. Rev. 49, S147–S160.CrossRefGoogle Scholar
Garcia-Mayoral, R. & Jimenez, J. 2011 Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369 (1940), 1412–1427.Google Scholar
Gaster, M. 1988 Is the dolphin a red herring? In Turbulence Management and Relaminarisation, pp. 285–304. Springer.CrossRefGoogle Scholar
Hama, F. R.1954 Boundary-Layer Characteristics for Smooth and Rough Surfaces. SNAME.Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.Google Scholar
Jimenez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59 (2), 308–323.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Krindel, P. & Silberberg, A. 1979 Flow through gel-walled tubes. J. Colloid Interface Sci. 71 (1), 39–50.Google Scholar
Krogstad, P. A., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough-and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.CrossRefGoogle Scholar
Krogstadt, P. A. & Antonia, R. A. 1999 Surface roughness effects in turbulent boundary layers. Exp. Fluids 27 (5), 450–460.Google Scholar
Kumaran, V. 1995 Stability of the flow of a fluid through a flexible tube at high Reynolds number. J. Fluid Mech. 302, 117–139.Google Scholar
Kumaran, V. 1996 Stability of inviscid flow in a flexible tube. J. Fluid Mech. 320, 1–17.Google Scholar
Kumaran, V. 1998a Stability of the flow of a fluid through a flexible tube at intermediate Reynolds number. J. Fluid Mech. 357, 123–140.Google Scholar
Kumaran, V. 1998b Stability of wall modes in a flexible tube. J. Fluid Mech. 362, 1–15.Google Scholar
Kumaran, V., Fredrickson, G. H. & Pincus, P. 1994 Flow induced instability of the interface between a fluid and a gel at low Reynolds number. J. Phys. II 4 (6), 893–911.Google Scholar
Kumaran, V. & Muralikrishnan, R. 2000 Spontaneous growth of fluctuations in the viscous flow of a fluid past a soft interface. Phys. Rev. Lett. 84 (15), 3310–3313.Google Scholar
Lahav, J., Eliezer, N. & Silberberg, A. 1973 Gel-walled cylindrical channels as models for the microcirculation: dynamics of flow. Biorheology 10 (4), 595–604.Google Scholar
Landahl, M. T. 1962 On the stability of a laminar incompressible boundary layer over a flexible surface. J. Fluid Mech. 13 (04), 609–632.Google Scholar
Lee, T., Fisher, M. & Schwarz, W. H. 1993 Investigation of the stable interaction of a passive compliant surface with a turbulent boundary layer. J. Fluid Mech. 257, 373–401.Google Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of d-and k-type roughness in a turbulent channel flow. Phys. Fluids 19 (12), 125101.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Djenidi, L. & Antonia, R. A. 2004 Structure of turbulent channel flow with square bars on one wall. Intl J. Heat Fluid Flow 25 (3), 384–392.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
Luo, H. & Bewley, T. R. 2003 Design, modeling, and optimization of compliant tensegrity fabrics for the reduction of turbulent skin friction. In Smart Structures and Materials, pp. 460–470. International Society for Optics and Photonics.Google Scholar
Luo, H. & Bewley, T. R. 2005 Accurate simulation of near-wall turbulence over a compliant tensegrity fabric. In Smart Structures and Materials, pp. 184–197. International Society for Optics and Photonics.Google Scholar
Min, T., Yoo, J. Y. & Choi, H. 2001 Effect of spatial discretization schemes on numerical solutions of viscoelastic fluid flows. J. Non-Newtonian Fluid Mech. 100 (1), 27–47.CrossRefGoogle Scholar
Nikuradse, J. 1933 Laws of flow in rough pipes. In VDI Forschungsheft. Citeseer.Google Scholar
Nikuradse, J.1950 Laws of flow in rough pipes. Tech. Rep. National Advisory Committee for Aeronautics Washington.Google Scholar
Orlandi, P. & Leonardi, S. 2006 Dns of turbulent channel flows with two-and three-dimensional roughness. J. Turbul. 7 (53), N73.Google Scholar
Orlandi, P. & Leonardi, S. 2008 Direct numerical simulation of three-dimensional turbulent rough channels: parameterization and flow physics. J. Fluid Mech. 606, 399–415.Google Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2006 Turbulent channel flow with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.Google Scholar
Orlandi, P., Leonardi, S., Tuzi, R. & Antonia, R. A. 2003 Direct numerical simulation of turbulent channel flow with wall velocity disturbances. Phys. Fluids 15 (12), 3587–3601.Google Scholar
Perot, B. & Moin, P. 1995a Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.Google Scholar
Perot, B. & Moin, P. 1995b Shear-free turbulent boundary layers. Part 2. New concepts for Reynolds stress transport equation modelling of inhomogeneous flows. J. Fluid Mech. 295, 229–245.CrossRefGoogle Scholar
Picano, F., Breugem, W. P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Pluvinage, F., Kourta, A. & Bottaro, A. 2014 Instabilities in the boundary layer over a permeable, compliant wall. Phys. Fluids 26 (8), 084103.Google Scholar
Quintard, M. & Whitaker, S. 1994 Transport in ordered and disordered porous media ii: generalized volume averaging. Trans. Porous Med. 14 (2), 179–206.Google Scholar
Rosti, M. E., Cortelezzi, L. & Quadrio, M. 2015 Direct numerical simulation of turbulent channel flow over porous walls. J. Fluid Mech. 784, 396–442.Google Scholar
Samanta, A., Vinuesa, R., Lashgari, I., Schlatter, P. & Brandt, L. 2015 Enhanced secondary motion of the turbulent flow through a porous square duct. J. Fluid Mech. 784, 681–693.Google Scholar
Shankar, V. & Kumaran, V. 1999 Stability of non-parabolic flow in a flexible tube. J. Fluid Mech. 395, 211–236.Google Scholar
Srivatsan, L. & Kumaran, V. 1997 Flow induced instability of the interface between a fluid and a gel. J. Phys. II 7 (6), 947–963.Google Scholar
Suga, K., Matsumura, Y., Ashitaka, Y., Tominaga, S. & Kaneda, M. 2010 Effects of wall permeability on turbulence. Intl J. Heat Fluid Flow 31, 974–984.Google Scholar
Sugiyama, K., Ii, S., Takeuchi, S., Takagi, S. & Matsumoto, Y. 2011 A full Eulerian finite difference approach for solving fluid–structure coupling problems. J. Comput. Phys. 230 (3), 596–627.Google Scholar
Sussman, M., Smereka, P. & Osher, S. 1994 A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 114 (1), 146–159.Google Scholar
Takeuchi, S., Yuki, Y., Ueyama, A. & Kajishima, T. 2010 A conservative momentum-exchange algorithm for interaction problem between fluid and deformable particles. Intl J. Numer. Meth. Fluids 64 (10–12), 1084–1101.Google Scholar
Tilton, N. & Cortelezzi, L. 2006 The destabilizing effects of wall permeability in channel flows: a linear stability analysis. Phys. Fluids 18 (5), 051702.Google Scholar
Tilton, N. & Cortelezzi, L. 2008 Linear stability analysis of pressure-driven flows in channels with porous walls. J. Fluid Mech. 604, 411–445.CrossRefGoogle Scholar
Tryggvason, G., Sussman, M. & Hussaini, M. Y. 2007 Immersed boundary methods for fluid interfaces. In Computational Methods for Multiphase Flow, Chap. 3. Cambridge University Press.Google Scholar
Verma, M. K. S. & Kumaran, V. 2013 A multifold reduction in the transition Reynolds number, and ultra-fast mixing, in a micro-channel due to a dynamical instability induced by a soft wall. J. Fluid Mech. 727, 407–455.Google Scholar
Zalesak, S. T. 1979 Fully multidimensional flux-corrected transport. J. Comput. Phys. 31, 335–362.CrossRefGoogle Scholar