Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-09T21:43:33.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical simulation of flow past a heated/cooled sphere

Published online by Cambridge University Press:  05 January 2012

Ryoichi Kurose ,
Mamiko Anami ,
Akitoshi Fujita  and
Satoru Komori
Ryoichi Kurose*
Affiliation:
Department of Mechanical Engineering and Science, and Advanced Research Institute of Fluid Science and Engineering, Kyoto University, Yoshida-honmachi, Sakyo-ku, Kyoto 606-8501, Japan
Mamiko Anami
Affiliation:
Department of Mechanical Engineering and Science, and Advanced Research Institute of Fluid Science and Engineering, Kyoto University, Yoshida-honmachi, Sakyo-ku, Kyoto 606-8501, Japan
Akitoshi Fujita
Affiliation:
Department of Mechanical Engineering and Science, and Advanced Research Institute of Fluid Science and Engineering, Kyoto University, Yoshida-honmachi, Sakyo-ku, Kyoto 606-8501, Japan
Satoru Komori
Affiliation:
Department of Mechanical Engineering and Science, and Advanced Research Institute of Fluid Science and Engineering, Kyoto University, Yoshida-honmachi, Sakyo-ku, Kyoto 606-8501, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

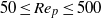The characteristics of flow past a heated/cooled sphere are investigated for particle Reynolds numbers in conditions with and without buoyancy by means of three-dimensional numerical simulation in which temperature dependence of fluid properties such as density and viscosity is exactly taken into account. The results show that in the absence of buoyancy, drag coefficients of the heated and cooled spheres are larger and smaller than those of the adiabatic case, respectively, and their Nusselt numbers are smaller and larger than the values estimated by a widely used empirical expression for predicting Nusselt numbers, respectively. In addition, the temperature difference between the sphere and ambient fluid strongly affects the flow separation points, size of vortex ring behind the sphere and Strouhal number for vortex shedding. These changes are attributed to the temperature dependence of fluid properties in the vicinity of the sphere. Even in the presence of buoyancy, the temperature dependence of fluid properties strongly affects the drag coefficient and Nusselt number and therefore the Boussinesq approximation becomes inapplicable as the temperature difference increases, regardless of the magnitude of the Richardson number.

JFM classification

Boundary Layers: Boundary layer structure Wakes/Jets: Separated flows Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 692 , 10 February 2012 , pp. 332 - 346
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baba, Y. & Kurose, R. 2008 Analysis snd flamelet modelling for spray combution. J. Fluid Mech. 612, 45–79.CrossRefGoogle Scholar
2.Bagchi, P. & Kottam, K. 2008 Effect of free stream isotropic turbulence on heat transfer from a sphere. Phys. Fluids 20, 073305.CrossRefGoogle Scholar
3.Beard, K. V. & Pruppacher, H. R. 1971 A wind tunnel investigation of the rate of evapouration of small water drops falling at terminal velocity in air. J. Atmos. Sci. 28, 1455–1464.2.0.CO;2>CrossRefGoogle Scholar
4.Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
5.Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic, republished by Dover, 2005.Google Scholar
6.Constantinescu, G. S. & Squires, K. D. 2003 LES and DES investigations of turbulent flow over a sphere at . Flow Turbul. Combust. 70, 267–298.CrossRefGoogle Scholar
7.Johnson, T. A. & Patel, V. C 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
8.Kee, R. J., Rupley, F. M. & Miller, J. A. 1994 The chemkin thermodynamic data base. Sandia Report SAND87, 8215B.Google Scholar
9.Kotouč, M., Bouchet, G. & Dušek, J. 2009 Drag and flow reversal in mixed convection past a heated sphere. Phys. Fluids 21, 054104.CrossRefGoogle Scholar
10.Kurose, R., Fujita, A. & Komori, S. 2009 Effect of relative humidity on heat transfer across the surface of an evapourating water droplet in air flow. J. Fluid Mech. 624, 57–67.CrossRefGoogle Scholar
11.Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.CrossRefGoogle Scholar
12.Kurose, R., Makino, H., Komori, S., Nakamura, M., Akamatsu, F. & Katsuki, M. 2003 Effects of outflow from surface of sphere on drag, shear lift, and scalar diffusion. Phys. Fluids 15, 2338–2351.CrossRefGoogle Scholar
13.Mansoorzadeh, S., Pain, C. C., De Oliveira, C. R. E. & Goddard, A. J. H. 1998 Finite element simulations of incompressible flow past a heated/cooled sphere. Intl J. Numer. Maths 28, 903–915.3.0.CO;2-O>CrossRefGoogle Scholar
14.Nakamura, M., Akamatsu, F., Kurose, R. & Katsuki, M. 2005 Combustion mechanism of liquid fuel spray in gaseous flame. Phys. Fluids 17, 123301.CrossRefGoogle Scholar
15.Rodriguez, I., Borell, R., Lehmkuhl, O., Segarra, P. & Oliva, A. 2011 Direct numerical simulation of the flow over a sphere at . J. Fluid Mech. 679, 263–287.CrossRefGoogle Scholar
16.Schiller, L. & Nauman, A. 1933 Über die grundledede berechnungen bei der schwerkraft-aufbereitung. Zeitschrift des Vereines Ceutscher Ingenieure 338, 325–357.Google Scholar
17.Sutherland, W. 1893 The viscosity of gases and molecular force. Phil. Mag. S.5, 36, 507–531.CrossRefGoogle Scholar
18.Taneda, S. 1956 Experimental investigation of the wake behind a sphere at low Reynolds numbers. J. Phys. Soc. Japan 11, 1104–1108.CrossRefGoogle Scholar