Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-17T20:12:45.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of wake flow regimes behind a high-speed rotating circular cylinder in steady flow

Published online by Cambridge University Press:  18 September 2019

Adnan Munir Open the ORCID record for Adnan Munir [Opens in a new window] ,
Ming Zhao Open the ORCID record for Ming Zhao [Opens in a new window] ,
Helen Wu  and
Lin Lu
Adnan Munir
Affiliation:
School of Computing, Engineering and Mathematics, Western Sydney University, Penrith, NSW, Australia
Ming Zhao*
Affiliation:
School of Computing, Engineering and Mathematics, Western Sydney University, Penrith, NSW, Australia
Helen Wu
Affiliation:
School of Computing, Engineering and Mathematics, Western Sydney University, Penrith, NSW, Australia
Lin Lu
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Flow around a high-speed rotating circular cylinder for 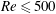$Re\leqslant 500$ is investigated numerically. The Reynolds number is defined as 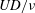$UD/\unicode[STIX]{x1D708}$ with 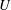$U$, 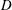$D$ and $\unicode[STIX]{x1D708}$ being the free-stream flow velocity, the diameter of the cylinder and the kinematic viscosity of the fluid, respectively. The aim of this study is to investigate the effect of a high rotation rate on the wake flow for a range of Reynolds numbers. Simulations are performed for Reynolds numbers of 100, 150, 200, 250 and 500 and a wide range of rotation rates from 1.6 to 6 with an increment of 0.2. Rotation rate is the ratio of the rotational speed of the cylinder surface to the incoming fluid velocity. A systematic study is performed to investigate the effect of rotation rate on the flow transition to different flow regimes. It is found that there is a transition from a two-dimensional vortex shedding mode to no vortex shedding mode when the rotation rate is increased beyond a critical value for Reynolds numbers between 100 and 200. Further increase in rotation rate results in a transition to three-dimensional flow which is characterized by the presence of finger-shaped (FV) vortices that elongate in the wake of the cylinder and very weak ring-shaped vortices (RV) that wrap the surface of the cylinder. The no vortex shedding mode is not observed at Reynolds numbers greater than or equal to 250 since the flow remains three-dimensional. As the rotation rate is increased further, the occurrence frequency and size of the ring-shaped vortices increases and the flow is dominated by RVs. The RVs become bigger in size and the flow becomes chaotic with increasing rotation rate. A detailed analysis of the flow structures shows that the vortices always exist in pairs and the strength of separated shear layers increases with the increase of rotation rate. A map of flow regimes on a plane of Reynolds number and rotation rate is presented.

JFM classification

Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 875 - 906
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badr, H., Coutanceau, M., Dennis, S. & Menard, C. 1990 Unsteady flow past a rotating circular cylinder at Reynolds numbers 103 and 104 . J. Fluid Mech. 220, 459–484.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Borazjani, I., Ge, L. & Sotiropoulos, F. 2008 Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. J. Comput. Phys. 227, 7587–7620.Google Scholar
Brede, M., Eckelmann, H. & Rockwell, D. 1996 On secondary vortices in the cylinder wake. Phys. Fluids 8, 2117–2124.Google Scholar
Carberry, J., Sheriden, J. & Rockwell, D. 2001 Forces and wake modes of an oscillating cylinder. J. Fluids Struct. 15, 523–532.Google Scholar
Chang, C. C. & Chern, R. L. 1991 Vortex shedding from an impulsively started rotating and translating circular cylinder. J. Fluid Mech. 233, 265–298.Google Scholar
Chew, Y. T., Cheng, M. & Luo, S. C. 1995 A numerical study of flow past a rotating circular cylinder using a hybrid vortex scheme. J. Fluid Mech. 299, 35–71.Google Scholar
Chou, M. H. 2000 Numerical study of vortex shedding from a rotating cylinder immersed in a uniform flow field. Intl J. Numer. Meth. Fluids 32, 545–567.Google Scholar
Diaz, F., Gavalda, J., Kawall, J. G., Keffer, J. F. & Giralt, F. 1983 Vortex shedding from a spinning cylinder. Phys. Fluids 26, 3454–3460.Google Scholar
El Akoury, R., Braza, M., Perrin, R., Harran, G. & Hoara, Y. 2008 The three-dimensional transition in the tlow around a totating tylinder. J. Fluid Mech. 607, 1–11.Google Scholar
Gioria, R. S., Meneghini, J. R., Aranha, J. A. P., Barbeiro, I. C. & Carmo, B. S. 2011 Effect of the domain spanwise periodic length on the flow around a circular cylinder. J. Fluids Struct. 27, 792–797.Google Scholar
Hammache, M. & Gharib, M. 1991 An experimental study of the parallel and oblique vortex shedding from circular cylinders. J. Fluid Mech. 232, 567–590.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kang, S. 2006 Laminar flow over a steadily rotating circular cylinder under the influence of uniform shear. Phys. Fluids 18, 047106.Google Scholar
Kang, S., Choi, H. & Lee, S. 1999 Laminar flow past a rotating circular cylinder. Phys. Fluids 11, 3312–3321.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Lam, K. 2009 Vortex shedding flow behind a slowly rotating circular cylinder. J. Fluids Struct. 25, 245–262.Google Scholar
Lei, C., Cheng, L. & Kavanagh, K. 2001 Spanwise length effects on three-dimensional modelling of flow over a circular cylinder. Comput. Meth. Appl. Mech. Engng 190, 2909–2923.Google Scholar
Lu, L., Qin, J. M., Teng, B. & Li, Y. C. 2011 Numerical investigations of lift suppression by feedback rotary oscillation of circular cylinder at low Reynolds number. Phys. Fluids 23, 033601.Google Scholar
Mittal, S. 2004 Three-dimensional instabilities in flow past a rotating cylinder. Trans. ASME J. Appl. Mech. 71, 89–95.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Navrose, Meena, J. & Mittal, S. 2015 Three-dimensional flow past a rotating cylinder. J. Fluid Mech. 766, 28–53.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.Google Scholar
Prandtl, L.1926 Application of the ‘Magnus effect’ to the wind propulsion of ships. NACA Tech. Mem., NACA-TM-367.Google Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013b Three-dimensionality in the wake of a rapidly rotating cylinder in a uniform flow. J. Fluid Mech. 730, 379–391.Google Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. NACA Tech. Rep. Mo. NACA-TR-1191.Google Scholar
Sotiropoulos, F. & Borazjani, I. 2009 A review of state-of-the-art numerical methods for simulating flow through mechanical heart valves. Med. Biol. Engng Comput. 47, 245–256.Google Scholar
Stojković, D., Breuer, M. & Durst, F. 2002 Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 14, 3160–3178.Google Scholar
Stojković, D., Schön, P., Breuer, M. & Durst, F. 2003 On the new vortex shedding mode past a rotating circular cylinder. Phys. Fluids 15, 1257–1260.Google Scholar
Tang, T. & Ingham, D. B. 1991 On steady flow past a rotating circular cylinder at Reynolds numbers 60 and 100. Comput. Fluids 19, 217–230.Google Scholar
Thompson, M., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Tokumaru, P. T. & Dimitakis, P. E. 1993 The lift of a cylinder executing rotary motions in a uniform flow. J. Fluid Mech. 255, 1–10.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.Google Scholar
Wu, J., Sheridan, J., Hourigan, K. & Soria, J. 1996a Shear layer vortices and longitudinal vortices in the near wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 169–174.Google Scholar
Wu, J., Sheridan, J., Welsh, M. C. & Hourigan, K. 1996b Three-dimensional vortex structures in a cylinder wake. J. Fluid Mech. 312, 201–222.Google Scholar
Wu, J., Sheridan, J., Welsh, M. C., Hourigan, K. & Thompson, M. C. 1994 Longitudinal vortex structures in a cylinder wake. Phys. Fluids 6, 2883–2885.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2009 Direct numerical simulation of three-dimensional flow past a yawed circular cylinder of infinite length. J. Fluids Struct. 25, 831–847.Google Scholar
Zhao, M., Thapa, J., Cheng, L. & Zhou, T. 2013 Three-dimensional transition of vortex shedding flow around a circular cylinder at right and oblique attacks. Phys. Fluids 25, 014105.Google Scholar