Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T19:56:22.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of turbulent features past different mechanical aortic valves

Published online by Cambridge University Press:  19 April 2022

A. Nitti Open the ORCID record for A. Nitti [Opens in a new window] ,
G. De Cillis Open the ORCID record for G. De Cillis [Opens in a new window]  and
M.D. de Tullio Open the ORCID record for M.D. de Tullio [Opens in a new window]
A. Nitti
Affiliation:
Department of Mechanics, Mathematics and Management, Polytechnic University of Bari, Via Re David 200, 70125, Bari, Italy
G. De Cillis
Affiliation:
Department of Mechanics, Mathematics and Management, Polytechnic University of Bari, Via Re David 200, 70125, Bari, Italy Ocean Predictions and Applications Division, Euro-Mediterranean Centre on Climate Change Foundation, Via Augusto Imperatore 16, 73100, Lecce, Italy
M.D. de Tullio*
Affiliation:
Department of Mechanics, Mathematics and Management, Polytechnic University of Bari, Via Re David 200, 70125, Bari, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

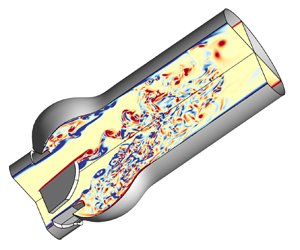
Flow through mechanical aortic valves (MAVs) has been constantly associated to higher haemolysis and platelet activation levels with respect to native valves, due to non-physiologic haemodynamic features. Both computational and experimental investigations have correlated the blood damage to augmented levels of turbulent stress downstream of MAVs. This study provides a computational estimation, drawn from high-resolution direct numerical simulations, of turbulent and fluctuating viscous stresses in three different MAV configurations, at subsequent stages of the cardiac cycle. The configurations comprise a St. Judes Medical Regent valve (SJMV), a Lapeyre-Triflo FURTIVA valve (LTFV) with three leaflets, and a SJMV with vortex generators (VGs). Non-standard configurations are expected to mitigate the mean stress level on blood constituents reducing the turbulent production. Computations are carried out by means of a finite-difference flow solver with a direct-forcing immersed boundary technique to handle fixed and moving bodies. The VGs are found to provide instabilities which corrupt the Kármán-like vortex shedding downstream of the leaflets, reducing the intensity of turbulent kinetic energy at the peak flow rate, thus lowering the local Reynolds shear stress. Conversely, the LTFV configuration provides comparable haemodynamic performance at peak flow rate but further reduced stress level in the deceleration phase. These interpretations are supported by probability density distributions from three-dimensional fields, and further corroborated by a pointwise mapping of the Taylor length scale and local energy spectra. The outcomes of this study might potentially be exploited to improve the design of new-generation MAVs, with the aim of decreasing the risk of thromboembolic complications.

JFM classification

Biological Fluid Dynamics: Biomedical flows Turbulent Flows: Turbulent transition Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 940 , 10 June 2022 , A43
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akutsu, T., Matsumoto, A. & Takahashi, K. 2011 In vitro study of the correlation between the aortic flow field affected by the bileaflet mechanical valves and coronary circulation. In 5th European Conference of the International Federation for Medical and Biological Engineering, pp. 769–772. Springer.CrossRefGoogle Scholar
Andersson, M. & Karlsson, M. 2021 Characterization of anisotropic turbulence behavior in pulsatile blood flow. Biomech. Model. Mechanobiol. 20 (2), 491–506.CrossRefGoogle ScholarPubMed
Antiga, L. & Steinman, D.A. 2009 Rethinking turbulence in blood. Biorheology 46 (2), 77–81.CrossRefGoogle ScholarPubMed
Banerjee, S., Krahl, R., Durst, F. & Zenger, C. 2007 Presentation of anisotropy properties of turbulence, invariants versus eigenvalue approaches. J. Turbul. 8, N32.CrossRefGoogle Scholar
Becsek, B., Pietrasanta, L. & Obrist, D. 2020 Turbulent systolic flow downstream of a bioprosthetic aortic valve: velocity spectra, wall shear stresses, and turbulent dissipation rates. Front. Physiol. 11, 577188.CrossRefGoogle ScholarPubMed
Belmabrouk, H. & Michard, M. 1998 Taylor length scale measurement by laser doppler velocimetry. Exp. Fluids 25 (1), 69–76.CrossRefGoogle Scholar
Bluestein, D., Rambod, E. & Gharib, M. 2000 Vortex shedding as a mechanism for free emboli formation in mechanical heart valves. J. Biomech. Engng 122 (2), 125–134.CrossRefGoogle ScholarPubMed
Caballero, A.D. & Laín, S.J.C.E. 2013 A review on computational fluid dynamics modelling in human thoracic aorta. Cardiovasc. Engng Technol. 4 (2), 103–130.CrossRefGoogle Scholar
Carrel, T., Dembitsky, W.P., de Mol, B., Obrist, D., Dreyfus, G., Meuris, B., Vennemann, B., Lapeyre, D. & Schaff, H. 2020 Non-physiologic closing of bi-leaflet mechanical heart prostheses requires a new tri-leaflet valve design. Intl J. Cardiol. 304, 125–127.CrossRefGoogle ScholarPubMed
Cerbus, R.T., Liu, C.-C., Gioia, G. & Chakraborty, P. 2020 Small-scale universality in the spectral structure of transitional pipe flows. Sci. Adv. 6 (4), eaaw6256.CrossRefGoogle ScholarPubMed
Dasi, L.P., Ge, L., Simon, H.A., Sotiropoulos, F. & Yoganathan, A.P. 2007 Vorticity dynamics of a bileaflet mechanical heart valve in an axisymmetric aorta. Phys. Fluids 19 (6), 067105.CrossRefGoogle Scholar
De Cillis, G., Cherubini, S., Semeraro, O., Leonardi, S. & De Palma, P. 2021 Pod-based analysis of a wind turbine wake under the influence of tower and nacelle. Wind Energy 24 (6), 609–633.CrossRefGoogle Scholar
De Vita, F., de Tullio, M.D. & Verzicco, R. 2016 Numerical simulation of the non-newtonian blood flow through a mechanical aortic valve. Theor. Comput. Fluid Dyn. 30 (1–2), 129–138.CrossRefGoogle Scholar
Ellis, J.T., Wick, T.M. & Yoganathan, A.P. 1998 Prosthesis-induced hemolysis: mechanisms and quantification of shear stress. J. Heart Valve Dis. 7 (4), 376–386.Google ScholarPubMed
Emory, M. & Iaccarino, G. 2014 Visualizing turbulence anisotropy in the spatial domain with componentality contours. In Center for Turbulence Research Annual Research Briefs, pp. 123–138.Google Scholar
Faghih, M.M. & Sharp, M.K. 2019 Modeling and prediction of flow-induced hemolysis: a review. Biomech. Model. Mechanobiol. 18 (4), 845–881.CrossRefGoogle ScholarPubMed
Flamini, V., DeAnda, A. & Griffith, B.E. 2016 Immersed boundary-finite element model of fluid–structure interaction in the aortic root. Theor. Comput. Fluid Dyn. 30 (1–2), 139–164.CrossRefGoogle ScholarPubMed
Fransson, J.H.M. & Talamelli, A. 2012 On the generation of steady streamwise streaks in flat-plate boundary layers. J. Fluid Mech. 698, 211–234.CrossRefGoogle Scholar
Gallegos, R.P., Rivard, A.L., Suwan, P.T., Black, S., Bertog, S., Steinseifer, U., Armien, A., Lahti, M. & Bianco, R.W. 2006 In-vivo experience with the triflo trileaflet mechanical heart valve. J. Heart Valve Dis. 15 (6), 791–799.Google ScholarPubMed
Ge, L., Dasi, L.P, Sotiropoulos, F. & Yoganathan, A.P 2008 Characterization of haemodynamic forces induced by mechanical heart valves: Reynolds vs viscous stresses. Ann. Biomed. Engng 36 (2), 276–297.CrossRefGoogle ScholarPubMed
Ghigo, A.R., Lagrée, P.-Y. & Fullana, J.-M. 2018 A time-dependent non-Newtonian extension of a 1D blood flow model. J. Non-Newtonian Fluid Mech. 253, 36–49.CrossRefGoogle Scholar
Ghista, D.N. 1976 Toward an optimum prosthetic trileaflet aortic-valve design. Med. Biol. Engng 14 (2), 122–129.CrossRefGoogle ScholarPubMed
Goldsmith, H.L., Marlow, J. & MacIntosh, F.C. 1972 Flow behaviour of erythrocytes-I. Rotation and deformation in dilute suspensions. Proc. R. Soc. Lond. B 182 (1068), 351–384.Google Scholar
Goldstone, A.B., Chiu, P., Baiocchi, M., Lingala, B., Patrick, W.L., Fischbein, M.P. & Woo, Y.J. 2017 Mechanical or biologic prostheses for aortic-valve and mitral-valve replacement. New Engl. J. Med. 377 (19), 1847–1857.CrossRefGoogle ScholarPubMed
Guivier-Curien, C., Deplano, V. & Bertrand, E. 2009 Validation of a numerical 3-D fluid–structure interaction model for a prosthetic valve based on experimental PIV measurements. Med. Engng Phys. 31 (8), 986–993.CrossRefGoogle ScholarPubMed
Ha, H., Kim, G.B., Kweon, J., Lee, S.J., Kim, Y.-H., Kim, N. & Yang, D.H. 2016 The influence of the aortic valve angle on the haemodynamic features of the thoracic aorta. Sci. Rep. 6, 32316.CrossRefGoogle ScholarPubMed
Hatoum, H. & Dasi, L.P. 2019 Reduction of pressure gradient and turbulence using vortex generators in prosthetic heart valves. Ann. Biomed. Engng 47 (1), 85–96.CrossRefGoogle ScholarPubMed
Hatoum, H., Maureira, P. & Dasi, L.P. 2020 A turbulence in vitro assessment of on-x and st jude medical prostheses. J. Thorac. Cardiovasc. Surg. 159 (1), 88–97.CrossRefGoogle Scholar
Haya, L. & Tavoularis, S. 2016 Effects of bileaflet mechanical heart valve orientation on fluid stresses and coronary flow. J. Fluid Mech. 806, 129–164.CrossRefGoogle Scholar
Hedayat, M., Asgharzadeh, H. & Borazjani, I. 2017 Platelet activation of mechanical versus bioprosthetic heart valves during systole. J. Biomech. 56, 111–116.CrossRefGoogle ScholarPubMed
Holmes, D.R. Jr., et al. 2016 Annual outcomes with transcatheter valve therapy: from the sts/acc TVT registry. Ann. Thorac. Surg. 101 (2), 789–800.CrossRefGoogle ScholarPubMed
Hsu, M.-C., Kamensky, D., Bazilevs, Y., Sacks, M.S. & Hughes, T.J.R. 2014 Fluid–structure interaction analysis of bioprosthetic heart valves: significance of arterial wall deformation. Comput. Mech. 54 (4), 1055–1071.CrossRefGoogle ScholarPubMed
Hung, T.C., Hochmuth, R.M., Joist, J.H. & Sutera, S.P. 1976 Shear-induced aggregation and lysis of platelets. ASAIO J. 22 (1), 285–290.Google ScholarPubMed
Hussain, A.K.M.F. & Reynolds, W.C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41 (2), 241–258.CrossRefGoogle Scholar
Isaacs, A.J., Shuhaiber, J., Salemi, A., Isom, O.W. & Sedrakyan, A. 2015 National trends in utilization and in-hospital outcomes of mechanical versus bioprosthetic aortic valve replacements. J. Thorac. Cardiovasc. Surg. 149 (5), 1262–1269.CrossRefGoogle ScholarPubMed
Jhun, C.-S., Stauffer, M.A., Reibson, J.D., Yeager, E.E., Newswanger, R.K., Taylor, J.O., Manning, K.B., Weiss, W.J. & Rosenberg, G. 2018 Determination of Reynolds shear stress level for hemolysis. ASAIO J. 64 (1), 63–69.CrossRefGoogle ScholarPubMed
Jin, G. & Braza, M. 1993 A nonreflecting outlet boundary condition for incompressible unsteady Navier–Stokes calculations. J. Comput. Phys. 107 (2), 239–253.CrossRefGoogle Scholar
Jones, S.A. 1995 A relationship between Reynolds stresses and viscous dissipation: implications to red cell damage. Ann. Biomed. Engng 23 (1), 21–28.CrossRefGoogle ScholarPubMed
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kim, S.H., Kim, H.J., Kim, J.B., Jung, S.-H., Choo, S.J., Chung, C.H. & Lee, J.W. 2019 Supra-annular versus intra-annular prostheses in aortic valve replacement: impact on haemodynamics and clinical outcomes. Interact. Cardiovasc. Thorac. Surg. 28 (1), 58–64.CrossRefGoogle ScholarPubMed
Kim, W., Choi, H., Kweon, J., Yang, D.H. & Kim, Y.-H. 2020 Effects of pannus formation on the flow around a bileaflet mechanical heart valve. PLoS ONE 15 (6), e0234341.CrossRefGoogle ScholarPubMed
Kleine, P., Perthel, M., Nygaard, H., Hansen, S.B., Paulsen, P.K., Riis, C. & Laas, J. 1998 Medtronic hall versus St. Jude medical mechanical aortic valve: downstream turbulences with respect to rotation in pigs. J. Heart Valve Dis. 7, 548–555.Google ScholarPubMed
Lee, J.H., Rygg, A.D., Kolahdouz, E.M., Rossi, S., Retta, S.M., Duraiswamy, N., Scotten, L.N., Craven, B.A. & Griffith, B.E. 2020 Fluid–structure interaction models of bioprosthetic heart valve dynamics in an experimental pulse duplicator. Ann. Biomed. Engng 48 (5), 1475–1490.CrossRefGoogle Scholar
Leverett, L.B., Hellums, J.D., Alfrey, C.P. & Lynch, E.C. 1972 Red blood cell damage by shear stress. Biophys. J. 12 (3), 257–273.CrossRefGoogle ScholarPubMed
Li, K.Y.C. 2019 Bioprosthetic heart valves: upgrading a 50-year old technology. Front. Cardiovasc. Med. 6, 47.CrossRefGoogle ScholarPubMed
Li, Q., Hegner, F. & Bruecker, C.H. 2020 Comparative study of wall-shear stress at the ascending aorta for different mechanical heart valve prostheses. J. Biomech. Engng 142 (1), 011006.CrossRefGoogle ScholarPubMed
Linde, T., Hamilton, K.F., Navalon, E.C., Schmitz-Rode, T. & Steinseifer, U. 2012 Aortic root compliance influences hemolysis in mechanical heart valve prostheses: an in-vitro study. Intl J. Artif. Organs 35 (7), 495–502.CrossRefGoogle Scholar
Liu, J.S., Lu, P.C. & Chu, S.H. 2000 Turbulence characteristics downstream of bileaflet aortic valve prostheses. J. Biomech. Engng 122 (2), 118–124.CrossRefGoogle ScholarPubMed
Lu, P.C., Lai, H.C. & Liu, J.S. 2001 A reevaluation and discussion on the threshold limit for hemolysis in a turbulent shear flow. J. Biomech. 34 (10), 1361–1364.CrossRefGoogle Scholar
Lumley, J.L. & Newman, G.R. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82 (1), 161–178.CrossRefGoogle Scholar
Malvern, L.E. 1969 Introduction to the Mechanics of a Continuous Medium. Prentice-Hall.Google Scholar
Mansour, N.N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.CrossRefGoogle Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.CrossRefGoogle Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.CrossRefGoogle Scholar
Moin, P. & Verzicco, R. 2016 On the suitability of second-order accurate discretizations for turbulent flow simulations. Eur. J. Mech. B/Fluids 55, 242–245.CrossRefGoogle Scholar
Morbiducci, U., Ponzini, R., Rizzo, G., Cadioli, M., Esposito, A., Montevecchi, F.M. & Redaelli, A. 2011 Mechanistic insight into the physiological relevance of helical blood flow in the human aorta: an in vivo study. Biomech. Model. Mechanobiol. 10 (3), 339–355.CrossRefGoogle ScholarPubMed
Murphy, D.W., Dasi, L.P., Vukasinovic, J., Glezer, A. & Yoganathan, A.P. 2010 Reduction of procoagulant potential of b-datum leakage jet flow in bileaflet mechanical heart valves via application of vortex generator arrays.J. Biomech. Engng. 132 (7), 071011.Google Scholar
Nitti, A., Kiendl, J., Reali, A. & de Tullio, M.D. 2020 An immersed-boundary/isogeometric method for fluid–structure interaction involving thin shells. Comput. Meth. Appl. Mech. Engng 364, 112977.CrossRefGoogle Scholar
Novostia 2019 Patient-benefits. https://www.novostia.com/patient-benefits.Google Scholar
Nyboe, C., Funder, J.A., Smerup, M.H., Nygaard, H. & Hasenkam, J.M. 2006 Turbulent stress measurements downstream of three bileaflet heart valve designs in pigs. Eur. J. Cardio-Thorac. Surg. 29 (6), 1008–1013.CrossRefGoogle ScholarPubMed
Orlandi, P. 2012 Fluid Flow Phenomena: A Numerical Toolkit, vol. 55. Springer Science & Business Media.Google Scholar
Orlanski, I. 1976 A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 21 (3), 251–269.CrossRefGoogle Scholar
Pai, R.G., Kapoor, N., Bansal, R.C. & Varadarajan, P. 2006 Malignant natural history of asymptomatic severe aortic stenosis: benefit of aortic valve replacement. Ann. Thorac. Surg. 82 (6), 2116–2122.CrossRefGoogle ScholarPubMed
Persillon, H. & Braza, M. 1998 Physical analysis of the transition to turbulence in the wake of a circular cylinder by three-dimensional Navier–Stokes simulation. J. Fluid Mech. 365, 23–88.CrossRefGoogle Scholar
Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.CrossRefGoogle Scholar
Pope, S.B. 2001 Turbulent flows. Cambridge University Press.CrossRefGoogle Scholar
Quinlan, N.J. & Dooley, P.N. 2007 Models of flow-induced loading on blood cells in laminar and turbulent flow, with application to cardiovascular device flow. Ann. Biomed. Engng 35 (8), 1347–1356.CrossRefGoogle ScholarPubMed
Ramstack, J.M., Zuckerman, L. & Mockros, L.F. 1979 Shear-induced activation of platelets. J. Biomech. 12 (2), 113–125.CrossRefGoogle ScholarPubMed
Reardon, M.J., et al. 2017 Surgical or transcatheter aortic-valve replacement in intermediate-risk patients. New Engl. J. Med. 376 (14), 1321–1331.CrossRefGoogle ScholarPubMed
Reul, H., Vahlbruch, A., Giersiepen, M., Schmitz-Rode, T.H., Hirtz, V. & Effert, S. 1990 The geometry of the aortic root in health, at valve disease and after valve replacement. J. Biomech. 23 (2), 181–191.CrossRefGoogle ScholarPubMed
Roudaut, R., Serri, K. & Lafitte, S. 2007 Thrombosis of prosthetic heart valves: diagnosis and therapeutic considerations. Heart 93 (1), 137–142.CrossRefGoogle ScholarPubMed
Sharp, M.K. & Mohammad, S.F. 1998 Scaling of hemolysis in needles and catheters. Ann. Biomed. Engng 26 (5), 788–797.CrossRefGoogle ScholarPubMed
Siconolfi, L., Camarri, S. & Fransson, J.H.M. 2015 Stability analysis of boundary layers controlled by miniature vortex generators. J. Fluid Mech. 784, 596–618.CrossRefGoogle Scholar
Siginer, D.A., De Kee, D. & Chhabra, R.P. 1999 Advances in the Flow and Rheology of Non-Newtonian Fluids. Elsevier.Google Scholar
Sotiropoulos, F. & Borazjani, I. 2009 A review of state-of-the-art numerical methods for simulating flow through mechanical heart valves. Med. Biol. Engng Comput. 47 (3), 245–256.CrossRefGoogle ScholarPubMed
St. Jude Medical, Inc. 2010 Pre-market approval application–summary of safety and effectiveness. SJM regent heart valve. Tech. Rep. P810002/S57. St. Jude Medical, Inc.Google Scholar
Sutera, S.P. 1977 Flow-induced trauma to blood cells. Circ. Res. 41 (1), 2–8.CrossRefGoogle ScholarPubMed
Taylor, G.I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164 (919), 476–490.CrossRefGoogle Scholar
Tezduyar, T.E. & Sathe, S. 2007 Modelling of fluid–structure interactions with the space–time finite elements: solution techniques. Intl J. Numer. Meth. Fluids 54 (6–8), 855–900.CrossRefGoogle Scholar
Tiederman, W.G., Privette, R.M. & Phillips, W.M. 1988 Cycle-to-cycle variation effects on turbulent shear stress measurements in pulsatile flows. Exp. Fluids 6 (4), 265–272.CrossRefGoogle Scholar
de Tullio, M.D., Cristallo, A., Balaras, E. & Verzicco, R. 2009 Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 622, 259–290.CrossRefGoogle Scholar
de Tullio, M.D., Nam, J., Pascazio, G., Balaras, E. & Verzicco, R. 2012 Computational prediction of mechanical hemolysis in aortic valved prostheses. Eur. J. Mech. B/Fluids 35, 47–53.CrossRefGoogle Scholar
de Tullio, M.D. & Pascazio, G. 2016 A moving-least-squares immersed boundary method for simulating the fluid–structure interaction of elastic bodies with arbitrary thickness. J. Comput. Phys. 325, 201–225.CrossRefGoogle Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Vanella, M. & Balaras, E. 2009 A moving-least-squares reconstruction for embedded-boundary formulations. J. Comput. Phys. 228 (18), 6617–6628.CrossRefGoogle Scholar
Vennemann, B., Rösgen, T., Heinisch, P.P. & Obrist, D. 2018 Leaflet kinematics of mechanical and bioprosthetic aortic valve prostheses. ASAIO J. 64 (5), 651–661.CrossRefGoogle ScholarPubMed
Vlachopoulos, C., O'Rourke, M. & Nichols, W.W. 2011 McDonald's Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles. CRC Press.CrossRefGoogle Scholar
Xu, F., Morganti, S., Zakerzadeh, R., Kamensky, D., Auricchio, F., Reali, A., Hughes, T.J.R., Sacks, M.S. & Hsu, M.-C. 2018 A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid–structure interaction analysis. Intl J. Numer. Meth. Biomed. Engng 34 (4), e2938.CrossRefGoogle ScholarPubMed
Yeung, P.-K. & Pope, S.B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar
Yilmaz, F. & Gundogdu, M.Y. 2008 A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions. Korea-Aust. Rheol. J. 20 (4), 197–211.Google Scholar
Yoganathan, A.P., He, Z. & Casey Jones, S. 2004 Fluid mechanics of heart valves. Annu. Rev. Biomed. Engng 6, 331–362.CrossRefGoogle ScholarPubMed
Yun, B.M., Dasi, L.P., Aidun, C.K. & Yoganathan, A.P. 2014 a Computational modelling of flow through prosthetic heart valves using the entropic Lattice–Boltzmann method. J. Fluid Mech. 743, 170–201.CrossRefGoogle Scholar
Yun, B.M., Dasi, L.P., Aidun, C.K. & Yoganathan, A.P. 2014 b Highly resolved pulsatile flows through prosthetic heart valves using the entropic Lattice–Boltzmann method. J. Fluid Mech. 754, 122–160.CrossRefGoogle Scholar
Yun, B.M., Wu, J., Simon, H.A., Arjunon, S., Sotiropoulos, F., Aidun, C.K. & Yoganathan, A.P. 2012 A numerical investigation of blood damage in the hinge area of aortic bileaflet mechanical heart valves during the leakage phase. Ann. Biomed. Engng 40 (7), 1468–1485.CrossRefGoogle ScholarPubMed
Zhu, C., Seo, J.-H. & Mittal, R. 2018 Computational modelling and analysis of haemodynamics in a simple model of aortic stenosis. J. Fluid Mech. 851, 23–49.CrossRefGoogle Scholar