Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T06:11:34.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of the water entry of cylinders without and with spin

Published online by Cambridge University Press:  02 February 2017

Areti Kiara ,
Ruben Paredes  and
Dick K. P. Yue
Areti Kiara
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Ruben Paredes
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K. P. Yue*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the water entry of horizontal cylinders with vertical impact velocity, either kept constant or freely falling, without and with spin, into quiescent water under the effect of gravity. We focus on the flow and cavity forming stages with non-dimensional submergence time $t$, Froude numbers 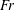$Fr$, spin ratios $\unicode[STIX]{x1D6FC}$ and mass ratios $m$, all of 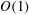$O(1)$. We develop numerical simulations using a modified smoothed particle hydrodynamics method to obtain predictions for the impact kinematics and dynamics. These are in detailed agreement with available experiments. We elucidate the evolutions of the free surface, contact point positions, flow field, forces and trajectories and their dependence on 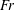$Fr$, $\unicode[STIX]{x1D6FC}$ and 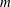$m$. We define and quantify the contact point location 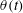$\unicode[STIX]{x1D703}(t)$ as a function of 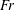$Fr$, clarifying the qualitative difference between sub- and supercritical 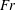$Fr$ and the observed absence of air-entrained trailing cavities at low 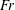$Fr$. By subtracting the buoyancy associated with 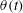$\unicode[STIX]{x1D703}(t)$, we show that, unlike the total drag, the remaining dynamic components are qualitatively similar for all 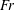$Fr$. For a freely falling cylinder, we show that the total drag can be predicted from the constant velocity case with the same instantaneous velocity, providing a simple way to predict its trajectory based on the latter. The presence of spin results in lift, even when the asymmetry in 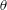$\unicode[STIX]{x1D703}$ is small. For fixed $\unicode[STIX]{x1D6FC}$, lift increases with subcritical 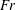$Fr$. For a freely falling cylinder, the lateral motion causes an appreciable asymmetry in 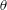$\unicode[STIX]{x1D703}$ and a reduction in lift.

JFM classification

Mathematical Foundations: Computational methods Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 814 , 10 March 2017 , pp. 131 - 164
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aristoff, J. M. & Bush, J. W. M. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.Google Scholar
Badr, H. M., Coutanceau, M., Menard, C. & Dennis, S. C. R. 1990 Unsteady flow past a rotating circular cylinder at Reynolds numbers 103 and 104 . J. Fluid Mech. 220, 459–484.CrossRefGoogle Scholar
Badr, H. M. & Dennis, S. C. R. 1985 Time-dependent viscous flow past an impulsively started rotating and translating circular cylinder. J. Fluid Mech. 158, 447–488.CrossRefGoogle Scholar
Badr, H. M., Dennis, S. C. R. & Young, P. J. S. 1989 Steady and unsteady flow past a rotating circular cylinder at low Reynolds numbers. Comput. Fluids 17, 579–609.CrossRefGoogle Scholar
Balsara, D. S. 1995 Von Neumann stability analysis of smoothed particle hydrodynamics – suggestions for optimal algorithms. J. Comput. Phys. 121, 357–372.Google Scholar
Battistin, D. & Iafrati, A. 2003 Hydrodynamic loads during water entry of two-dimensional and axisymmetric bodies. J. Fluid Struct. 17, 643–664.Google Scholar
Birkhoff, G. 2012 Jets, Wakes, and Cavities. Elsevier.Google Scholar
Campbell, I. M. C. & Weynberg, P. A.1980 Measurement of parameters affecting slamming. Tech. Rep. 440. University of Southampton: Wolfson Unit for Marine Technology and Industrial Aerodynamics.Google Scholar
Chen, Y.-M., Ou, Y.-R. & Pearlstein, A. J. 1993 Development of the wake behind a circular cylinder impulsively started into rotatory and rectilinear motion. J. Fluid Mech. 253, 449–484.Google Scholar
Cheng, M. & Luo, L.-S. 2007 Characteristics of two-dimensional flow around a rotating circular cylinder near a plane wall. Phys. Fluids 19, 063601,1–17.CrossRefGoogle Scholar
Chuang, S.-L. 1966 Experiments on flat-bottom slamming. J. Ship Res. 10, 10–17.Google Scholar
Colagrossi, A., Antuono, M. & Le Touzé, D. 2009 Theoretical considerations on the free-surface role in the smoothed-particle-hydrodynamics model. Phys. Rev. E 79, 056701.Google Scholar
Colagrossi, A. & Landrini, M. 2003 Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 191, 448–475.Google Scholar
Colicchio, G., Greco, M., Miozzi, M. & Lugni, C. 2009 Numerical investigation of the water-entry and water-exit of a circular cylinder. In 24th Intl. Workshop on Water Waves and Floating Bodies, Zelenogorsk, Russia, April 19–22.Google Scholar
Coutanceau, M. & Menard, C. 1985 Influence of rotation on the near-wake development behind an impulsively started circular cylinder. J. Fluid Mech. 158, 399–446.CrossRefGoogle Scholar
Dehnen, W. & Aly, H. 2012 Improving convergence in Smoothed Particle Hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 425, 1068–1082.Google Scholar
Ding, H., Chen, B.-Q., Liu, H.-R., Zhang, C.-Y., Gao, P. & Lu, X.-Y. 2015 On the contact-line pinning in cavity formation during solid–liquid impact. J. Fluid Mech. 783, 504–525.Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.Google Scholar
Faltinsen, O. M. 1990 Sea Loads on Ships and Offshore Structures. Cambridge University Press.Google Scholar
Glasheen, J. W. & McMahon, T. A. 1996 A hydrodynamic model of locomotion in the basilisk lizard. Nature 380 (6572), 340–341.CrossRefGoogle Scholar
Gomez-Gesteira, M., Rogers, B. D., Dalrymple, R. A. & Crespo, A. J. C. 2010 State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 48, 6–27.Google Scholar
Greenhow, M. 1988 Water-entry and -exit of a horizontal circular cylinder. Appl. Ocean Res. 10, 191–198.Google Scholar
Greenhow, M. & Lin, W.-M.1983 Nonlinear free surface effects: experiments and theory. Tech. Rep. 83–19, MIT Internal Report.Google Scholar
Gurevich, M. I. 2014 The Theory of Jets in an Ideal Fluid, vol. 93. Elsevier.Google Scholar
Hagiwara, K. & Yuhara, T. 1976 Fundamental study of wave impact loads on ship bow. J. Soc. Nav. Archit. Japan 14, 73–85.Google Scholar
Hicks, P. D., Ermanyuk, E. V., Gavrilov, N. V. & Purvis, R. 2012 Air trapping at impact of a rigid sphere onto a liquid. J. Fluid Mech. 695, 310–320.CrossRefGoogle Scholar
von Kármán, T.1929 The impact on seaplane floats during landing. NACA Tech. Rep. 321.Google Scholar
Kiara, A.2010 Analysis of the smoothed particle hydrodynamics method for free-surface flows. PhD thesis, MIT.Google Scholar
Kiara, A., Hendrickson, K. & Yue, D. K. P. 2013a SPH for incompressible free-surface flows. Part I: error analysis of the basic assumptions. Comput. Fluids 86, 611–624.CrossRefGoogle Scholar
Kiara, A., Hendrickson, K. & Yue, D. K. P. 2013b SPH for incompressible free-surface flows. Part II: performance of a modified SPH method. Comput. Fluids 86, 510–536.CrossRefGoogle Scholar
Labraga, L., Kahissim, G., Keirsbulck, L. & Beaubert, F. 2007 An experimental investigation of the separation points on a circular rotating cylinder in cross flow. Trans. ASME J. Fluids Engng 129, 1203–1211.Google Scholar
Lee, M., Longoria, R. G. & Wilson, D. E. 1997 Cavity dynamics in high-speed water entry. Phys. Fluids 9, 540–550.CrossRefGoogle Scholar
Lin, M.-C. & Shieh, L.-D. 1997a Flow visualization and pressure characteristics of a cylinder for water impact. Appl. Ocean Res. 19, 101–112.Google Scholar
Lin, M.-C. & Shieh, L.-D. 1997b Simultaneous measurements of water impact on a two-dimensional body. Fluid Dyn. Res. 19, 125–148.Google Scholar
Liu, G. R. & Liu, M. B. 2003 Smoothed Particle Hydrodynamics a Meshfree Particle Method. World Scientific.Google Scholar
Marrone, S., Colagrossi, A., Antuono, M., Colicchio, G. & Graziani, G. 2013 An accurate SPH modeling of viscous flows around bodies at low and moderate Reynolds numbers. J. Comput. Phys. 245, 456–475.CrossRefGoogle Scholar
Martin-Alcantara, A., Sanmiguel-Rojas, E. & Fernandez-Feria, R. 2015 On the development of lift and drag in a rotating and translating cylinder. J. Fluid Struct. 54, 868–885.Google Scholar
Maruzewski, P., Le Touzé, D., Oger, G. & Avellan, F. 2010 SPH high-performance computing simulations of rigid solids impacting the free-surface of water. J. Hydraul. Res. 48, 126–134.CrossRefGoogle Scholar
May, A. 1951 Effect of surface condition of a sphere on its water-entry cavity. J. Appl. Phys. 22, 1219–1222.Google Scholar
May, A.1975 Water entry and the cavity-running behavior of missiles. Tech. Rep. SEAHAC/TR 75–2. Naval Surface Weapons Center.Google Scholar
Mei, X., Liu, Y. & Yue, D. K. P. 1999 On the water impact of general two-dimensional sections. Appl. Ocean Res. 21, 1–15.CrossRefGoogle Scholar
Miao, G.1989 Hydrodynamic forces and dynamic responses of circular cylinders in wave zones. PhD thesis, The Norwegian Institute of Technology, Trondheim.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Moghisi, M. & Squire, P. T. 1981 An experimental investigation of the initial force of impact on a sphere striking a liquid surface. J. Fluid Mech. 108, 133–146.CrossRefGoogle Scholar
Molteni, D. & Colagrossi, A. 2009 A simple procedure to improve the pressure evaluation in hydrodynamic context using the SPH. Comput. Phys. Commun. 180, 861–872.Google Scholar
Monaghan, J. J. 1994 Simulating free surface flows with SPH. J. Comput. Phys. 110, 399–406.Google Scholar
Monaghan, J. J. 2012 Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 44, 323–346.Google Scholar
Morris, J. P., Fox, P. J. & Zhu, Y. 1997 Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 136, 214–226.Google Scholar
Oger, G., Doring, M., Alessandrini, B. & Ferrant, P. 2006 Two-dimensional SPH simulations of wedge water entries. J. Comput. Phys. 213, 803–822.Google Scholar
Saghatchi, R., Ghazanfarian, J. & Gorji-Bandpy, M. 2014 Numerical simulation of water-entry and sedimentation of an elliptic cylinder using smoothed-particle hydrodynamics method. Trans. ASME J. Offshore Mech. Arctic Engng 136, 031801–031810.CrossRefGoogle Scholar
Stacey, R. 1994 New finite-difference methods for free-surfaces with a stability analysis. Bull. Seismol. Soc. Am. 84, 171–184.Google Scholar
Sun, H. & Faltinsen, O. M. 2006 Water impact of horizontal circular cylinders and cylindrical shells. Appl. Ocean Res. 28, 299–311.Google Scholar
Swegle, J. W., Hicks, D. L. & Attaway, S. W. 1995 Smoothed Particle Hydrodynamics stability analysis. J. Comput. Phys. 116, 123–134.Google Scholar
Techet, A. H. & Truscott, T. T. 2011 Water entry of spinning hydrophobic and hydrophilic spheres. J. Fluid Struct. 27, 716–726.Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Takano, Y. 2004 Impact jetting by a solid sphere. J. Fluid Mech. 499, 139–148.Google Scholar
Truscott, T. T., Epps, B. P. & Belden, J. 2014 Water entry of projectiles. Annu. Rev. Fluid Mech. 46, 355–378.Google Scholar
Truscott, T. T., Epps, B. P. & Techet, A. H. 2012 Unsteady forces on spheres during free-surface water entry. J. Fluid Mech. 704, 173–210.Google Scholar
Truscott, T. T. & Techet, A. H. 2009a A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres. Phys. Fluids 21, 121703.Google Scholar
Truscott, T. T. & Techet, A. H. 2009b Water entry of spinning spheres. J. Fluid Mech. 625, 135–165.Google Scholar
Veen, D. J. & Gourlay, T. P. 2009 An investigation of slam events in two dimensions using Smoothed Particle Hydrodynamics. In 10th Int. Conference on Fast Sea Transportation (FAST 2009), Athens, Greece, National Technical University of Athens.Google Scholar
Vella, D., Lee, D.-G. & Kim, H.-Y. 2006 Sinking of a horizontal cylinder. Langmuir 22, 2972–2974.Google Scholar
Wagner, H. 1932 Über stoß-und gleitvorgänge an der oberfläche von flüssigkeiten. Z. Angew. Math. Mech. 12, 193–215.Google Scholar
Weymouth, G. D. & Yue, D. K. P. 2010 Conservative volume-of-fluid method for free-surface simulations on Cartesian-grids. J. Comput. Phys. 229, 2853–2865.Google Scholar
Weymouth, G. D. & Yue, D. K. P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid-body interaction problems. J. Comput. Phys. 230, 6233–6247.Google Scholar
Yan, H., Liu, Y., Kominiarczuk, J. & Yue, D. K. P. 2009 Cavity dynamics in water entry at low Froude numbers. J. Fluid Mech. 641, 441–461.CrossRefGoogle Scholar
Yung, T.-W., Sandström, R. E., He, H. & Minta, M. K. 2010 On the physics of vapor liquid interaction during impact on solids. J. Ship Res. 54, 174–183.CrossRefGoogle Scholar
Zhang, Y., Zou, Q., Greaves, D., Reeve, D., Hunt-Raby, A., Graham, D., James, P. & Lv, X. 2010 A level set immersed boundary method for water entry and exit. Comput. Phys. Commun. 8, 265–288.CrossRefGoogle Scholar
Zhao, R. & Faltinsen, O. 1993 Water entry of two-dimensional bodies. J. Fluid Mech. 246, 593–612.Google Scholar
Zhu, X., Faltinsen, O. M. & Hu, C. 2007 Water entry and exit of a horizontal circular cylinder. J. Offshore Mech. Arctic Engng 129, 253–264.Google Scholar