Published online by Cambridge University Press: 23 October 2014
Multiple mechanisms for the regeneration of hairpin-like coherent flow structures in transitional and turbulent boundary layers have been proposed in the published literature, but a complete understanding of the typical topologies of coherent structures observed in the literature has not yet been achieved. To contribute to this understanding, a numerical study is performed of a turbulent spot triggered in a zero-pressure-gradient laminar boundary layer by a pulsed, transverse jet. Two direct numerical simulations (DNS) capture the growth of the spot into a mature turbulent region containing a large number of coherent vortical flow structures. The boundary-layer Reynolds number based on the test-surface streamwise length is 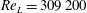 $\mathit{Re}_{L}=309\,200$. The internal structure of the spot is characterized by densely spaced packets of hairpin vortices. Lateral growth of the spot occurs as new hairpin vortices form along the spanwise edges of the spot. The formation of these hairpin vortices is attributed to unstable shear layers that develop in the streamwise–spanwise plane due to the wall-normal motions induced by the streamwise oriented legs of hairpin vortices within the spot. Results are presented that highlight the mechanism by which the instability of such shear layers forms wavepackets of hairpin vortices; how the formation of these vortices produces a flow environment that promotes the creation of new hairpin vortices; and how the newly created hairpin vortices impact the production of turbulence kinetic energy in the flow region surrounding the spot. A quantitative description of the hairpin-vortex regeneration mechanism based on the transport of the instantaneous vorticity vector is presented to illustrate how the velocity and vorticity fields interact with the local strain rates to promote the growth of coherent vortical structures. The simulation results also shed light on a mechanism that seems to have a dominant influence on the formation of the calmed region in the wake of the turbulent spot.
$\mathit{Re}_{L}=309\,200$. The internal structure of the spot is characterized by densely spaced packets of hairpin vortices. Lateral growth of the spot occurs as new hairpin vortices form along the spanwise edges of the spot. The formation of these hairpin vortices is attributed to unstable shear layers that develop in the streamwise–spanwise plane due to the wall-normal motions induced by the streamwise oriented legs of hairpin vortices within the spot. Results are presented that highlight the mechanism by which the instability of such shear layers forms wavepackets of hairpin vortices; how the formation of these vortices produces a flow environment that promotes the creation of new hairpin vortices; and how the newly created hairpin vortices impact the production of turbulence kinetic energy in the flow region surrounding the spot. A quantitative description of the hairpin-vortex regeneration mechanism based on the transport of the instantaneous vorticity vector is presented to illustrate how the velocity and vorticity fields interact with the local strain rates to promote the growth of coherent vortical structures. The simulation results also shed light on a mechanism that seems to have a dominant influence on the formation of the calmed region in the wake of the turbulent spot.