Published online by Cambridge University Press: 12 November 2018
The role of free-stream turbulence (FST) in the hydrodynamic instability mechanisms and transition to turbulence in laminar separation bubbles (LSBs) was investigated using direct numerical simulations (DNS). Towards this end, a set of highly resolved DNS have been carried out, where isotropic FST fluctuations with intensities from 0.1 % to 3 % are introduced to investigate the relevant physical mechanisms governing the interaction of separation and transition in LSBs. For disturbance-free simulations, i.e. without FST, laminar–turbulent transition involves a Kelvin–Helmholtz (KH) instability of the separated shear layer. For LSBs subjected to FST, vortical FST fluctuations penetrate the approaching attached laminar boundary layer upstream of the separation location and induce slowly growing low-frequency disturbances, so-called Klebanoff (K) modes, which cause a spanwise modulation with a distinct spanwise wavelength. Simultaneously, the FST enhances the initial levels of instability waves with frequencies in the frequency range of the KH instability, but at much smaller amplitude levels compared to the K-modes. Results from the calculations based on the linearized Navier–Stokes equations and comparison with DNS results reveal that the K-mode exhibits exponential growth in the separated shear layer until it reaches a peak amplitude. At the same time, two-dimensional (2D) disturbance waves are also exponentially amplified, in fact at larger growth rate compared to the K-mode, due to the primary (convective) shear-layer instability mechanism until they saturate downstream of the peak amplitude associated with the K-mode. Therefore, based on detailed spectral analysis and modal decompositions for the separation bubbles investigated, the transition process is the result of two different mechanisms: (i) strong amplification of high-frequency (order of the shedding frequency), essentially 2D or weakly oblique fluctuating disturbances and (ii) low-frequency, three-dimensional K-modes caused by FST. Depending on the intensity of the FST, one of these mechanisms would dominate the transition process, or both mechanisms act together and contribute simultaneously. The net effect of these two events is an acceleration of transition for an increased level of FST intensity, which in turn leads to a reduction of the extent of the separation bubble in streamwise and wall-normal directions. The ‘roll-up’ into spanwise large-scale vortical structures resulting from the shear-layer instability, and the eventual breakdown of these structures, strongly contribute to the reattachment process. The spanwise coherence of these ‘rollers’ deteriorates due to the presence of large-amplitude K-modes, thus effectively weakening their strength for high levels of FST intensities (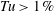 $Tu>1\,\%$).
$Tu>1\,\%$).