Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T22:20:02.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of flow and turbulence structure through and around a circular array of rigid cylinders

Published online by Cambridge University Press:  06 July 2015

Kyoungsik Chang  and
George Constantinescu
Kyoungsik Chang
Affiliation:
Department of Aeromechanical Engineering, Hanseo University, 356-706, South Korea
George Constantinescu*
Affiliation:
Department of Civil and Environmental Engineering, The University of Iowa, IA 52246, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This numerical study investigates flow and turbulence structure through and around a circular array of solid circular cylinders of diameter 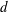$d$. The region containing the array of rigid cylinders resembles a porous circular cylinder of diameter 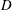$D$. The porous cylinder Reynolds number defined with the steady incoming flow velocity is 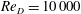$\mathit{Re}_{D}=10\,000$. Fully three-dimensional (3D) large eddy simulations (LES) are conducted to study the effects of the volume fraction of solids of the porous cylinder (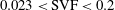$0.023<\text{SVF}<0.2$) and 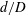$d/D$ on the temporal variation and mean values of the drag/lift forces acting on the solid cylinders and on the porous cylinder. The effects of the bleeding flow through the circular porous cylinder on the wake structure and the influence of the SVF and 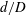$d/D$ on the onset of flow three-dimensionality within or downstream of the porous cylinder and transition to turbulence are discussed. Results are compared with experimental data, predictions of theoretical models available in the literature and also with the canonical case of a solid cylinder (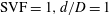$\text{SVF}=1,d/D=1$). Three-dimensional LES predict that large-scale wake billows are shed in the wake of the porous cylinder for 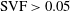$\text{SVF}>0.05$, similar to the von Karman vortex street observed for solid cylinders. As the SVF decreases, the length of the separated shear layers (SSLs) of the porous cylinder and the distance from the back of the porous cylinder at which wake billows form increase. For sufficiently low volume fractions of solids (e.g. 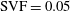$\text{SVF}=0.05$, 0.023), no wake billows are shed and the interactions among the wakes of the solid cylinders are weak. Even for 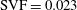$\text{SVF}=0.023$, SSLs containing large-scale turbulent eddies form on the two sides of the porous cylinder, but their ends cannot interact to generate wake billows. In both regimes, the force acting on some of the solid cylinders within the array is highly unsteady. As opposed to results obtained based on 2D simulations, no intermediate regime in which the force acting on the solid cylinders is close to steady is present. Interestingly, an energetic low frequency corresponding to a Strouhal number defined with the diameter of the porous cylinder of approximately 0.2 is present within the porous cylinder and near-wake regions not only for cases where wake billows are generated but also for cases where no wake billows form. In the latter cases, this frequency is due to an instability acting on the SSLs which induces in-phase large-scale undulatory deformations of the two SSLs. A combined drag parameter for the porous cylinder 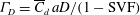${\it\Gamma}_{D}=\overline{C}_{d}\,aD/(1-\text{SVF})$ is introduced, where 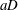$aD$ is the non-dimensional frontal area per unit volume of the porous cylinder. This parameter characterizes by how much the velocity of the bleeding flow at the back of the porous cylinder is reduced compared with the incoming flow velocity for a given total drag force acting on the porous cylinder. Results from simulations conducted with different values of the SVF, 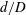$d/D$ and mean time-averaged solid cylinder streamwise drag parameter, 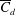$\overline{C}_{d}$, show that 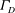${\it\Gamma}_{D}$ increases monotonically with increasing 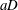$aD$. Several ways of defining the spatial extent of the wake region in a less ambiguous way are proposed.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 161 - 199
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, D. J. & Hall, C. D. 1980 Drag of yawed pile groups at low Reynolds numbers. J. Waterways Port Coast. Ocean Div. ASCE 106, 229–238.CrossRefGoogle Scholar
Ball, D. J., Stansby, P. K. & Allison, N. 1996 Modelling shallow water flow around pile groups. Proc. ICE-Water Maritime Energy 118 (4), 226–236.Google Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.Google Scholar
Bennett, S. J., Pirim, T. & Barkdoll, B. D. 2002 Using simulated emergent vegetation to alter stream flow direction within a straight experimental channel. Geomorphology 44, 115–126.Google Scholar
Bennett, S. J., Wu, W., Alonso, C. V. & Wang, S. S. 2008 Modeling fluvial response to in-stream woody vegetation: implications for stream corridor restoration. Earth Surf. Process. Landf. 33, 890–909.Google Scholar
Castro, I. P. 1971 Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 46, 599–609.CrossRefGoogle Scholar
Chang, K., Constantinescu, G. & Park, S. O. 2007 The purging of a neutrally buoyant or a dense miscible contaminant from a rectangular cavity. Part II: the case of an incoming fully turbulent overflow. ASCE J. Hydraul. Engng 133 (4), 373–385.Google Scholar
Chang, K. S. & Constantinescu, G. 2013 Coherent structures in developing flow over 2D dunes. Water Resour. Res. 49, 2446–2460.CrossRefGoogle Scholar
Chang, K. S., Constantinescu, G. & Park, S. O. 2006 Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J. Fluid Mech. 561, 113–145.Google Scholar
Chen, D. & Jirka, G. H. 1995 Experimental study of plane turbulent wakes in a shallow water layer. Fluid Dyn. Res. 16, 11–41.CrossRefGoogle Scholar
Chen, Z., Ortiz, A., Zong, L. & Nepf, H. 2012 The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 48, W09517.Google Scholar
Constantinescu, G. 2014 LES of lock-exchange compositional gravity currents: a brief review of some recent results. Environ. Fluid Mech. 14, 295–317.Google Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569, 185–207.Google Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex indentification in turbulence. J. Turbul. 1, doi:10.1088/1468-5248/1/1/011.Google Scholar
Ermanyuk, E. V. & Gavrilov, N. V. 2005a Interaction of an internal gravity current with a submerged circular cylinder. J. Appl. Mech. Tech. Phys. 46 (2), 216–223.Google Scholar
Ermanyuk, E. V. & Gavrilov, N. V. 2005b Interaction of an internal gravity current with an obstacle on the channel bottom. J. Appl. Mech. Tech. Phys. 46 (4), 489–495.CrossRefGoogle Scholar
Furukawa, K., Wolanski, E. & Mueller, H. 1997 Currents and sediment transport in mangrove forests. Estuar. Coast. Shelf Sci. 44, 301–310.Google Scholar
Gonzalez-Juez, E., Meiburg, E. & Constantinescu, G. 2009 Gravity currents impinging on bottom mounted square cylinders: flow fields and associated forces. J. Fluid Mech. 631, 65–102.Google Scholar
Gonzalez-Juez, E., Meiburg, E., Tokyay, T. & Constantinescu, G. 2010 Gravity current flow past a circular cylinder: forces and wall shear stresses and implications for scour. J. Fluid Mech. 649, 69–102.Google Scholar
Huang, Z. & Keffer, J. F. 1996 Development of structure within the turbulent wake of a porous body. Part 1. The initial formation region. J. Fluid Mech. 329, 103–115.Google Scholar
Jamali, M., Zhang, X. & Nepf, H. 2008 Exchange flow between a canopy and open water. J. Fluid Mech. 611, 237–254.CrossRefGoogle Scholar
King, A. T., Tinoco, R. O. & Cowen, E. A. 2012 A ${\it\kappa}{-}{\it\varepsilon}$ turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows. J. Fluid Mech. 701, 1–39.Google Scholar
Kirkil, G. & Constantinescu, G. 2010 Flow and turbulence structure around an in-stream rectangular cylinder with scour hole. Water Resour. Res. 46, W11549.CrossRefGoogle Scholar
Kirkil, G., Constantinescu, G. & Ettema, R. 2009 DES investigation of turbulence and sediment transport at a circular pier with scour hole. J. Hydraul. Engng 135 (11), 888–901.Google Scholar
Lam, K., Li, J. Y. & So, R. M. C. 2003 Force coefficients and Strouhal numbers of four cylinders in cross flow. J. Fluids Struct. 18, 305–324.Google Scholar
Munson, B. B., Okiishi, T., Huebsch, W. & Rothmayer, A. P. 2012 Fundamentals of Fluid Mechanics, 7th edn. Wiley; ISBN 13:978-1118399712.Google Scholar
Neary, V. S., Constantinescu, S. G., Benett, S. J. & Diplas, P. 2012 Effects of vegetation on turbulence, sediment and stream morphology. ASCE J. Hydraul. Engng 138 (9), 765–776.Google Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.Google Scholar
Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.CrossRefGoogle Scholar
Norberg, C. 1993 Flow around rectangular cylinders: pressure forces and wake frequencies. J. Wind Engng Ind. Aerodyn. 49, 187–196.Google Scholar
Norberg, C. 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96.CrossRefGoogle Scholar
Pierce, C. D. & Moin, P.2001 Progress-variable approach for large-eddy simulation of turbulent combustion. Mech. Eng. Dept. Rep. TF-80. Stanford University, California, USA.Google Scholar
Sand-Jensen, K. & Pedersen, M. L. 2008 Streamlining of plant patches in streams. Freshwat. Biol. 53, 714–726.Google Scholar
Takemura, T. & Tanaka, N. 2007 Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 39, 694–710.Google Scholar
Tanino, Y. & Nepf, H. M. 2008 Lateral dispersion in random cylinder arrays at high Reynolds number. J. Fluid Mech. 600, 339–371.CrossRefGoogle Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2011 Lock exchange gravity currents with a high volume of release propagating over an array of obstacles. J. Fluid Mech. 672, 570–605.Google Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2012 Tail structure and bed friction velocity distribution of gravity currents propagating over an array of obstacles. J. Fluid Mech. 694, 252–291.CrossRefGoogle Scholar
Tokyay, T., Constantinescu, G. & Meiburg, E. 2014 Lock exchange gravity currents with a low volume of release propagating over an array of obstacles. J. Geophys. Res. Oceans 119, 2752–2768.CrossRefGoogle Scholar
Vandenbruwaene, W., Temmerman, S., Bouma, T. J., Klaassen, P. C., de Vries, M. B., Callaghan, D. P., van Steeg, P., Dekker, F., van Duren, L. A., Martini, E., Balke, T., Biermans, G., Schoelynck, J. & Meire, P. 2011 Flow interaction with dynamic vegetation patches: implications for biogeomorphic evolution of a tidal landscape. J. Geophys. Res. 116, F01008.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Ann. Rev. Fluid Mech. 28, 477–539.Google Scholar
Xiyun, L. & Guocan, L. 2002 A large eddy simulation of the near wake of a circular cylinder. Acta Mechanica Sin. 18, 18–30.CrossRefGoogle Scholar
Yuksel Ozan, A., Constantinescu, G. & Hogg, A. J. 2015 Full-depth lock exchange gravity currents with a high volume of release propagating through arrays of cylinders. J. Fluid Mech. 675, 544–575.Google Scholar
Zdravkovich, M. M. 1997 Flow Around Circular Cylinders – Volume 1 Fundamentals. Oxford University Press.Google Scholar
Zong, L. & Nepf, H. 2011 Spatial distribution of deposition within a patch of vegetation. Water Resour. Res. 47, W03516.Google Scholar
Zong, L. & Nepf, H. 2012 Vortex development behind a finite porous obstruction in a channel. J. Fluid Mech. 691, 368–391.Google Scholar

Chang et al. supplementary movie

Animation showing nondimensional vertical vorticity field in the wake of a porous cylinder. a) SVF=0.2, antisymmetric shedding, von Karman vortex street is present b) SVF=0.05, symmetric shedding, no von Karman vortex street forms

Download Chang et al. supplementary movie(Video)
Video 3.4 MB

Chang et al. supplementary movie

Animations showing the nondimensional vertical vorticity distribution through the array of cylinders. a) SVF=0.2; b) SVF=0.05. The movie visualizes the vortical content of the bleeding flow and the wake-to-cylinder interactions for a case with a high SVF and a case with a low SVF.

Download Chang et al. supplementary movie(Video)
Video 3.6 MB