Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-24T22:33:33.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation and modelling of acoustically excited flow through a circular orifice backed by a hexagonal cavity

Published online by Cambridge University Press:  18 January 2012

Qi Zhang  and
Daniel J. Bodony
Qi Zhang
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Illinois 61801, USA
Daniel J. Bodony*
Affiliation:
Department of Aerospace Engineering, University of Illinois at Urbana-Champaign, Illinois 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Resolved simulations of the sound-induced flow through a circular orifice with a 0.99 mm diameter are examined. The orifice is backed by a hexagonal cavity and is a local model for acoustic liners commonly used for aeroengine noise reduction. The simulation data identify the role the orifice wall boundary layers play in determining the orifice discharge coefficient which, in time-domain models, is an important indicator of nonlinearity. It is observed that when the liner behaviour is not well described by linear models, the orifice boundary layers contain secondary vorticity generated from its separation from the corner on the high-pressure side of the orifice. Quantitative comparisons of the simulation-predicted impedance match available data for incident sound of 130 dB amplitude at frequencies from 1.5 to 3.0 kHz. At amplitudes of 140–160 dB, the simulation impedance is in agreement with analytical predictions when using simulation-measured quantities, including the discharge coefficient and root-mean-square velocity through the orifice, although no experimental data for this liner exist at these conditions. The simulation data are used to develop two time-domain models for the acoustic impedance wherein the velocity profile through the orifice is modelled as the product of the fluid velocity and a presumed radial shape, . 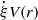The models perform well, predicting the in-orifice velocity and pressure, and the impedance, except for the most nonlinear cases where it is seen that the assumed shape can affect the backplate pressure predictions. These results suggest that future time-domain models that take the velocity profile into account, by modelling the boundary layer thickness and assuming a velocity profile shape, may be successful in predicting the nonlinear response of the liner.

JFM classification

Acoustics: Aeroacoustics Acoustics: Noise control Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 693 , 25 February 2012 , pp. 367 - 401
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Berland, J., Bogey, C., Marsden, O. & Bailly, C. 2007 High-order, low dispersive and low dissipative explicit schemes for multiple-scale and boundary problems. J. Comput. Phys. 224, 637–662.CrossRefGoogle Scholar
2. Bodony, D. J. 2006 Analysis of sponge zones for computational fluid mechanics. J. Comput. Phys. 212, 681–702.CrossRefGoogle Scholar
3. Bodony, D. J. 2010 Accuracy of the simultaneous-approximation-term boundary condition for time-dependent problems. J. Sci. Comput. 43 (1), 118–133.CrossRefGoogle Scholar
4. Bogey, C. & Bailly, C. 2004 A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 194, 194–214.CrossRefGoogle Scholar
5. Charwat, A. F. & Walker, B. E. 1983 The velocity perturbations above the orifice of an acoustically excited cavity in grazing flow. J. Fluid Mech. 128, 413–426.CrossRefGoogle Scholar
6. Cummings, A. & Eversman, W. 1983 High amplitude acoustic transmission through duct terminations: theory. J. Sound Vib. 91 (4), 503–518.CrossRefGoogle Scholar
7. Dean, P. D. 1974 An in situ method of wall acoustic impedance measurement in flow ducts. J. Sound Vib. 34 (1), 97–130.CrossRefGoogle Scholar
8. Dwyer, H. A. 1968 Calculation of unsteady leading-edge boundary layers. AIAA J. 6 (12), 2447–2448.CrossRefGoogle Scholar
9. Glezer, A. & Amitay, M. 2002 Synthetic jets. Annu. Rev. Fluid Mech. 34, 503–529.CrossRefGoogle Scholar
10. Hersh, A. S., Walker, B. E. & Celano, J. W. 2003 Helmholtz resonator impedance model. Part 1. Nonlinear behaviour. AIAA J. 41 (5), 795–808.CrossRefGoogle Scholar
11. Howe, M. S. 1979 On the theory of unsteady high Reynolds number flow through a circular aperture. Proc. R. Soc. Lond. A 366, 205–223.Google Scholar
12. Howe, M. S. 2003 Theory of Vortex Sound. Cambridge University Press.Google Scholar
13. Howerton, B. M. & Parrott, T. L. 2009 Validation of an acoustic impedance prediction model for skewed resonators. AIAA Paper 2009-3143, presented at the 15th AIAA/CEAS Aeroacoustics Conference and Exhibit.CrossRefGoogle Scholar
14. Hubbard, H. H.  (Ed.) 1995 Aeroacoustics of Flight Vehicles: Theory and Practice. Vol. 1: Noise Sources. Vol. 2: Noise Control. Acoustical Society of America.Google Scholar
15. Ingard, U. 1953 On the theory and design of acoustic resonators. J. Acoust. Soc. Am. 25 (6), 1037–1061.CrossRefGoogle Scholar
16. Ingard, U. & Labate, S. 1950 Acoustic circulation effects and the nonlinear impedance of orifices. J. Acoust. Soc. Am. 22, 211–219.CrossRefGoogle Scholar
17. Jing, X. & Sun, X. 2002 Sound-excited flow and acoustic nonlinearity at an orifice. Phys. Fluids 14 (1), 268–276.CrossRefGoogle Scholar
18. Jing, X., Sun, X., Wu, J. & Meng, K. 2001 Effect of grazing flow on the acoustic impedance of an orifice. AIAA J. 39 (8), 1478–1484.CrossRefGoogle Scholar
19. Jones, M. G., Parrott, T. L. & Watson, W. R. 2003 Comparison of acoustic impedance eduction techniques for locally-reacting liners. AIAA Paper 2003-3306, presented at the 9th AIAA/CEAS Aeroacoustics Conference.CrossRefGoogle Scholar
20. Jones, M. G., Smith, W. R., Parrott, T. L. & Smith, C. D. 2004 a Design and evaluation of modifications to the NASA Langley flow impedance tube. AIAA Paper 2004-2837, presented at the 10th AIAA/CEAS Aeroacoustics Conference.CrossRefGoogle Scholar
21. Jones, M. G., Watson, W. R., Tracy, M. B. & Parrott, T. L. 2004b Comparison of two waveguide methods for educing liner impedance in grazing flow. AIAA J. 42 (2), 232–240.CrossRefGoogle Scholar
22. Lighthill, M. J. 1952 On sound generated aerodynamically. Part I. General theory. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
23. Melling, T. H. 1973 The acoustic impedance of perforates at medium and high sound pressure levels. J. Sound Vib. 29, 1–65.CrossRefGoogle Scholar
24. Motsinger, R. E. & Kraft, R. E. 1995 Design and performance of duct acoustic treatment. In Aeroacoustics of Flight Vehicles: Theory and Practice (ed. Hubbard, H. H. ), vol. II. pp. 165–206. Acoustical Society of America.Google Scholar
25. Petrie, A. M. & Huntley, I. D. 1980 The acoustic output produced by a steady airflow through a corrugated duct. J. Sound Vib. 70 (1), 1–9.CrossRefGoogle Scholar
26. Phillips, W. R. C. 1996 On a class of unsteady boundary layers of finite extent. J. Fluid Mech. 319, 151–170.CrossRefGoogle Scholar
27. Posey, J. W., Tinetti, A. F. & Dunn, M. H. 2006 The low-noise potential of distributed propulsion on a catamaran aircraft. AIAA Paper 2006-2622, presented at the 12th AIAA/CEAS Aeroacoustics Conference and Exhibit, Cambridge, MA.CrossRefGoogle Scholar
28. Rayleigh, Lord 1894 The Theory of Sound, 1945th edn. Dover.Google Scholar
29. Rice, E. J. 1976 A theoretical study of the acoustic impedance of orifices in the presence of a steady grazing flow. Technical Memorandum NASA TM X-71903.CrossRefGoogle Scholar
30. Roche, J.-M., Vuillot, F., Leylekian, L., Delattre, G., Piot, E. & Simon, F. 2010 Numerical and experimental study of resonant liners aeroacoustic absorption under grazing flow. Presented at the 16th AIAA/CEAS Aeroacoustics Conference.CrossRefGoogle Scholar
31. Sherer, S. E. & Scott, J. N. 2005 High-order compact finite-difference methods on general overset grids. J. Comput. Phys. 210 (2), 459–496.CrossRefGoogle Scholar
32. Sherer, S. E., Visbal, M. R. & Galbraith, M. C. 2006 Automated preprocessing tools for use with a high-order overset-grid algorithm. AIAA Paper 2006-1147.CrossRefGoogle Scholar
33. Sivian, L. J. 1935 Acoustic impedance of small orifices. J. Acoust. Soc. Am. 7, 94–101.CrossRefGoogle Scholar
34. Strand, B. 1994 Summation by parts for finite difference approximations for . J. Comput. Phys. 110, 47–67.CrossRefGoogle Scholar
35. Svärd, M., Carpenter, M. H. & Nordström, J. 2007 A stable high-order finite difference scheme for the compressible Navier–Stokes equations, far-field boundary conditions. J. Comput. Phys. 225, 1020–1038.CrossRefGoogle Scholar
36. Svärd, M. & Nordström, J. 2008 A stable high-order finite difference scheme for the compressible Navier–Stokes equations: no-slip wall boundary conditions. J. Comput. Phys. 227, 4805–4824.CrossRefGoogle Scholar
37. Tam, C. K. W., Ju, H., Jones, M. G., Watson, W. R. & Parrott, T. L. 2010 A computational and experimental study of resonators in three dimensions. J. Sound Vib. 329, 5164–5193.CrossRefGoogle Scholar
38. Tam, C. K. W., Ju, H. & Walker, B. E. 2008 Numerical simulation of a slit resonator in a grazing flow under acoustic excitation. J. Sound Vib. 313, 449–471.CrossRefGoogle Scholar
39. Tam, C. K. W. & Kurbatskii, K. A. 2000 Microfluid dynamics and acoustics of resonant liners. AIAA J. 38 (8), 1331–1339.CrossRefGoogle Scholar
40. Tam, C. K. W., Kurbatskii, K. A., Ahuja, K. K. & Gaeta, R. J. Jr 2001 A numerical and experimental investigation of the dissipation mechanisms of resonant acoustic liners. J. Sound Vib. 245 (3), 545–557.CrossRefGoogle Scholar
41. Tang, P. K. & Sirignano, W. A. 1973 Theory of a generalized Helmholtz resonator. J. Sound Vib. 26 (2), 247–262.CrossRefGoogle Scholar
42. Watson, W. R. & Jones, M. G. 2009 Impedance eduction in ducts with higher-order modes and flow. AIAA Paper 2009-3236, presented at the 15th AIAA/CEAS Aeroacoustics Conference and Exhibit.CrossRefGoogle Scholar
43. Watson, W. R., Jones, M. G. & Parrott, T. L. 2005 A quasi-3-D theory for impedance eduction in uniform grazing flow. AIAA Paper 2005-2848, presented at the 11th AIAA/CEAS Aeroacoustics Conference and Exhibit.CrossRefGoogle Scholar
44. White, F. M. 1991 Viscous Fluid Flow, 2nd edn. McGraw-Hill.Google Scholar
45. Zhang, Q. & Bodony, D. J. 2011 a Direct numerical simulation of three dimensional honeycomb liner with circular apertures. AIAA Paper 2011-0843, presented at the 49th Aerospace Sciences Meeting & Exhibit.CrossRefGoogle Scholar
46. Zhang, Q. & Bodony, D. J. 2011b Numerical simulation of two-dimensional acoustic liners with high speed grazing flow. AIAA J. 49 (2), 365–382.CrossRefGoogle Scholar
47. Zinn, B. T. 1970 A theoretical study of nonlinear damping by Helmholtz resonators. J. Sound Vib. 13 (3), 347–356.CrossRefGoogle Scholar
48. Zorumski, W. E. & Tester, B. J. 1976 Prediction of the acoustic impedance of duct liners. Technical Memorandum X-73951. NASA.Google Scholar