Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hammoud, Mohamad Abed El Rahman
Titi, Edriss S.
Hoteit, Ibrahim
and
Knio, Omar
2022.
CDAnet: A Physics‐Informed Deep Neural Network for Downscaling Fluid Flows.
Journal of Advances in Modeling Earth Systems,
Vol. 14,
Issue. 12,
Li, Jian
Tian, Mengdan
and
Li, Yi
2022.
Synchronizing large eddy simulations with direct numerical simulations via data assimilation.
Physics of Fluids,
Vol. 34,
Issue. 6,
Piroozmand, Pasha
Brenner, Oliver
and
Jenny, Patrick
2023.
Dimensionality reduction for regularization of sparse data-driven RANS simulations.
Journal of Computational Physics,
Vol. 492,
Issue. ,
p.
112404.
Cato, Arthur Shiniti
Volpiani, Pedro Stefanin
Mons, Vincent
Marquet, Olivier
and
Sipp, Denis
2023.
Comparison of different data-assimilation approaches to augment RANS turbulence models.
Computers & Fluids,
Vol. 266,
Issue. ,
p.
106054.
Rybchuk, A
Martínez-Tossas, L A
Hamilton, N
Doubrawa, P
Vijayakumar, G
Hassanaly, M
Kuhn, M B
and
Zalkind, D S
2023.
A baseline for ensemble-based, time-resolved inflow reconstruction for a single turbine using large-eddy simulations and latent diffusion models.
Journal of Physics: Conference Series,
Vol. 2505,
Issue. 1,
p.
012018.
Li, Sen
He, Chuangxin
Wang, Weizhe
and
Liu, Yingzheng
2023.
Flow enhancement from wall pressure observations: A compressible continuous adjoint data assimilation model.
Physics of Fluids,
Vol. 35,
Issue. 11,
Rybchuk, Alex
Hassanaly, Malik
Hamilton, Nicholas
Doubrawa, Paula
Fulton, Mitchell J.
and
Martínez-Tossas, Luis A.
2023.
Ensemble flow reconstruction in the atmospheric boundary layer from spatially limited measurements through latent diffusion models.
Physics of Fluids,
Vol. 35,
Issue. 12,
Hasegawa, Yuta
Onodera, Naoyuki
Asahi, Yuuichi
Ina, Takuya
Imamura, Toshiyuki
and
Idomura, Yasuhiro
2023.
Continuous data assimilation of large eddy simulation by lattice Boltzmann method and local ensemble transform Kalman filter (LBM-LETKF).
Fluid Dynamics Research,
Vol. 55,
Issue. 6,
p.
065501.
Martinez, Vincent R.
2024.
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
p.
1.
Thompson, Craig
Cadambi Padmanaban, Uttam
Ganapathisubramani, Bharathram
and
Symon, Sean
2024.
The effect of variations in experimental and computational fidelity on data assimilation approaches.
Theoretical and Computational Fluid Dynamics,
Vol. 38,
Issue. 3,
p.
431.
He, Chuangxin
Zeng, Xin
Wang, Peng
Wen, Xin
and
Liu, Yingzheng
2024.
Four-dimensional variational data assimilation of a turbulent jet for super-temporal-resolution reconstruction.
Journal of Fluid Mechanics,
Vol. 978,
Issue. ,
Kotsiopoulou, Maria
and
Bouris, Demetri
2024.
Nudging based computational wind engineering simulation of the Atmospheric Boundary Layer.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 244,
Issue. ,
p.
105627.
Li, Rui
Song, Baiyang
Chen, Yaoran
Jin, Xiaowei
Zhou, Dai
Han, Zhaolong
Chen, Wen-Li
and
Cao, Yong
2024.
Deep learning reconstruction of high-Reynolds-number turbulent flow field around a cylinder based on limited sensors.
Ocean Engineering,
Vol. 304,
Issue. ,
p.
117857.
Carlson, Elizabeth
Larios, Adam
and
Titi, Edriss S.
2024.
Super-Exponential Convergence Rate of a Nonlinear Continuous Data Assimilation Algorithm: The 2D Navier–Stokes Equation Paradigm.
Journal of Nonlinear Science,
Vol. 34,
Issue. 2,
Plogmann, Justin
Brenner, Oliver
and
Jenny, Patrick
2024.
Spectral adjoint-based assimilation of sparse data in unsteady simulations of turbulent flows.
Physics of Fluids,
Vol. 36,
Issue. 10,
Kellaris, Konstantinos
Pallas, Nikolaos Petros
and
Bouris, Demetri
2024.
Numerical calculation of the turbulent flow past a surface mounted cube with assimilation of PIV data.
Measurement Science and Technology,
Vol. 35,
Issue. 1,
p.
015301.
Ling, Yuenong
and
Lozano-Duran, Adrian
2025.
Numerically Consistent Data-Driven Subgrid-Scale Model via Data Assimilation and Machine Learning.
Villiers, Raphaël
Mons, Vincent
Sipp, Denis
Lamballais, Eric
and
Meldi, Marcello
2025.
Enhancing Unsteady Reynolds-Averaged Navier–Stokes Modelling from Sparse Data Through Sequential Data Assimilation and Machine Learning.
Flow, Turbulence and Combustion,
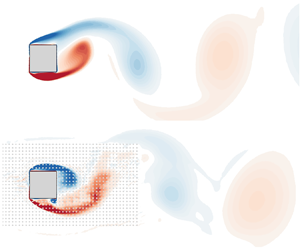
 $Re=22\,000$ based on temporally resolved but spatially sparse velocity data and solving the unsteady Reynolds-averaged Navier–Stokes (URANS) equations. Flow reconstruction from sparse data is achieved through the application of a nudging data assimilation technique. It involves the introduction of a feedback control term in the momentum equations which allows us to drive URANS predictions towards reference data, which are here extracted from a direct numerical simulation. Such a data assimilation approach induces negligible supplementary computational cost compared with that of a standard URANS simulation. The influence of the spatial resolution of the reference data on the reconstruction performances is systematically investigated. Using a spacing of the order of one cylinder length between data points, we already observe synchronisation of the low-frequency vortex shedding between the full reference flow and the one that is estimated by URANS. The present data assimilation procedure allows us to compensate for deficiencies in standard URANS calculations and leads to a significant decrease in temporal and spectral errors as computed by spectral proper orthogonal decomposition. Furthermore, high accuracy in terms of mean-flow prediction by URANS is achieved. When considering spacings between measurements that are of the order of the wavelength of the Kelvin–Helmholtz vortices, such phenomena in the shear layers at the top and bottom of the cylinder are correctly estimated, while they are not self-sustained in standard URANS. The influence of the structure of the feedback control term in the data assimilation procedure is also investigated.
$Re=22\,000$ based on temporally resolved but spatially sparse velocity data and solving the unsteady Reynolds-averaged Navier–Stokes (URANS) equations. Flow reconstruction from sparse data is achieved through the application of a nudging data assimilation technique. It involves the introduction of a feedback control term in the momentum equations which allows us to drive URANS predictions towards reference data, which are here extracted from a direct numerical simulation. Such a data assimilation approach induces negligible supplementary computational cost compared with that of a standard URANS simulation. The influence of the spatial resolution of the reference data on the reconstruction performances is systematically investigated. Using a spacing of the order of one cylinder length between data points, we already observe synchronisation of the low-frequency vortex shedding between the full reference flow and the one that is estimated by URANS. The present data assimilation procedure allows us to compensate for deficiencies in standard URANS calculations and leads to a significant decrease in temporal and spectral errors as computed by spectral proper orthogonal decomposition. Furthermore, high accuracy in terms of mean-flow prediction by URANS is achieved. When considering spacings between measurements that are of the order of the wavelength of the Kelvin–Helmholtz vortices, such phenomena in the shear layers at the top and bottom of the cylinder are correctly estimated, while they are not self-sustained in standard URANS. The influence of the structure of the feedback control term in the data assimilation procedure is also investigated.


