Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Caupin, Frédéric
2015.
Escaping the no man's land: Recent experiments on metastable liquid water.
Journal of Non-Crystalline Solids,
Vol. 407,
Issue. ,
p.
441.
Ohl, Siew-Wan
and
Ohl, Claus-Dieter
2015.
Handbook of Ultrasonics and Sonochemistry.
p.
1.
Ohl, Siew-Wan
and
Ohl, Claus-Dieter
2016.
Handbook of Ultrasonics and Sonochemistry.
p.
99.
Stan, Claudiu A.
Willmott, Philip R.
Stone, Howard A.
Koglin, Jason E.
Liang, Mengning
Aquila, Andrew L.
Robinson, Joseph S.
Gumerlock, Karl L.
Blaj, Gabriel
Sierra, Raymond G.
Boutet, Sébastien
Guillet, Serge A. H.
Curtis, Robin H.
Vetter, Sharon L.
Loos, Henrik
Turner, James L.
and
Decker, Franz-Josef
2016.
Negative Pressures and Spallation in Water Drops Subjected to Nanosecond Shock Waves.
The Journal of Physical Chemistry Letters,
Vol. 7,
Issue. 11,
p.
2055.
Li, Buxuan
Gu, Youwei
and
Chen, Min
2017.
An experimental study on the cavitation of water with dissolved gases.
Experiments in Fluids,
Vol. 58,
Issue. 12,
Wang, Peng
Gao, Wei
Wilkerson, Justin
Liechti, Kenneth M.
and
Huang, Rui
2017.
Cavitation of water by volume-controlled stretching.
Extreme Mechanics Letters,
Vol. 11,
Issue. ,
p.
59.
Fu, Qiang
Liu, Gang
Wang, Xiuli
and
Zhu, Rongsheng
2018.
Cavitation of dissolved oxygen liquid water under negative pressure.
Molecular Simulation,
Vol. 44,
Issue. 18,
p.
1501.
Oguri, Ryota
and
Ando, Keita
2018.
Cavitation bubble nucleation induced by shock-bubble interaction in a gelatin gel.
Physics of Fluids,
Vol. 30,
Issue. 5,
Veysset, D.
Gutiérrez-Hernández, U.
Dresselhaus-Cooper, L.
De Colle, F.
Kooi, S.
Nelson, K. A.
Quinto-Su, P. A.
and
Pezeril, T.
2018.
Single-bubble and multibubble cavitation in water triggered by laser-driven focusing shock waves.
Physical Review E,
Vol. 97,
Issue. 5,
Lyu, Xiuxiu
Pan, Shucheng
Hu, Xiangyu
and
Adams, Nikolaus A.
2018.
Numerical investigation of homogeneous cavitation nucleation in a microchannel.
Physical Review Fluids,
Vol. 3,
Issue. 6,
Bruning, M. A.
Costalonga, M.
Snoeijer, J. H.
and
Marin, A.
2019.
Turning Drops into Bubbles: Cavitation by Vapor Diffusion through Elastic Networks.
Physical Review Letters,
Vol. 123,
Issue. 21,
Rapet, Julien
Quinto-Su, Pedro A.
and
Ohl, Claus-Dieter
2020.
Cavitation Inception from Transverse Waves in a Thin Liquid Gap.
Physical Review Applied,
Vol. 14,
Issue. 2,
Gutiérrez-Hernández, Ulisses J.
De Colle, Fabio
Ohl, Claus-Dieter
and
Quinto-Su, Pedro A.
2021.
Transient time-delay focusing of shock waves in thin liquids.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Požar, Tomaž
Agrež, Vid
and
Petkovšek, Rok
2021.
Laser-induced cavitation bubbles and shock waves in water near a concave surface.
Ultrasonics Sonochemistry,
Vol. 73,
Issue. ,
p.
105456.
Ishikawa, Tatsumasa
Nishida, Hiroyuki
and
Tagawa, Yoshiyuki
2022.
Numerical Investigation on Influence of Number of Bubbles on Laser-Induced Microjet.
Water,
Vol. 14,
Issue. 22,
p.
3707.
Horvat, Darja
Agrež, Vid
Požar, Tomaž
Starman, Bojan
Halilovič, Miroslav
and
Petkovšek, Rok
2022.
Laser-induced shock-wave-expanded nanobubbles in spherical geometry.
Ultrasonics Sonochemistry,
Vol. 89,
Issue. ,
p.
106160.
Bempedelis, Nikolaos
and
Ventikos, Yiannis
2022.
A sharp-interface model for grid-resolved cavitating flows.
International Journal of Multiphase Flow,
Vol. 149,
Issue. ,
p.
103968.
Yang, Zhi
Bao, Hengzhu
Dai, Lunan
Zhang, Hongchao
and
Lu, Jian
2023.
Experimental investigation of nanosecond laser-induced shock waves in water using multiple excitation beams.
Optics Express,
Vol. 31,
Issue. 13,
p.
21845.
Avni, Orr
Dagan, Yuval
Bar-Kohany, Tali
and
Sher, Eran
2023.
Bubble dynamics under negative pressures: A missing link?.
Thermal Science and Engineering Progress,
Vol. 46,
Issue. ,
p.
102162.
Rosselló, Juan Manuel
Reese, Hendrik
Raman, K. Ashoke
and
Ohl, Claus-Dieter
2023.
Bubble nucleation and jetting inside a millimetric droplet.
Journal of Fluid Mechanics,
Vol. 968,
Issue. ,
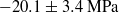 $- 20. 1\pm 3. 4~\mathrm{MPa} $ is extracted from the measured probabilities and the calculated minimum pressures.
$- 20. 1\pm 3. 4~\mathrm{MPa} $ is extracted from the measured probabilities and the calculated minimum pressures.