Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T17:43:00.812Z Has data issue: false hasContentIssue false
  • English
  • Français

Nozzle external geometry as a boundary condition for the azimuthal mode selection in an impinging underexpanded jet

Published online by Cambridge University Press:  11 January 2019

Joel L. Weightman ,
Omid Amili ,
Damon Honnery ,
Daniel Edgington-Mitchell Open the ORCID record for Daniel Edgington-Mitchell [Opens in a new window]  and
Julio Soria Open the ORCID record for Julio Soria [Opens in a new window]
Joel L. Weightman*
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Omid Amili
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis MN 55455, USA
Damon Honnery
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Daniel Edgington-Mitchell
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Julio Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

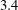The role of the external boundary conditions of the nozzle surface on the azimuthal mode selection of impinging supersonic jets is demonstrated for the first time. Jets emanating from thin- and infinite-lipped nozzles at a nozzle pressure ratio of $3.4$ and plate spacing of 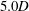$5.0D$, where 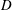$D$ is the nozzle exit diameter, are investigated using high resolution particle image velocimetry (PIV) and acoustic measurements. Proper orthogonal decomposition is applied to the PIV fields and a difference in dominant instability mode is found. To investigate possible explanations for the change in instability mode, additional nozzle external boundary conditions are investigated, including the addition of acoustic dampening foam. A difference in acoustic feedback path is suggested to be the cause for the change in dominant azimuthal modes between the flows. This is due to the thin-lip case containing a feedback path that is concluded to be closed exclusively by a reflection from the nozzle base surface, rather than directly to the nozzle lip. The ability of the flow to form a feedback path that maximises the impingement tone gain is discussed with consideration of the numerous acoustic feedback paths possible for the given nozzle external boundary conditions.

JFM classification

Acoustics: Aeroacoustics Aerodynamics: High-speed flow Acoustics: Jet noise
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 421 - 448
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barone, M. F. & Lele, S. K. 2005 Receptivity of the compressible mixing layer. J. Fluid Mech. 540, 301–335.Google Scholar
Beneddine, S., Mettot, C. & Sipp, D. 2015 Global stability analysis of underexpanded screeching jets. Eur. J. Mech. (B/Fluids) 49, 392–399.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.Google Scholar
Bogey, C. & Gojon, R. 2017 Feedback loop and upwind-propagating waves in ideally expanded supersonic impinging round jets. J. Fluid Mech. 823, 562–591.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (04), 775–816.Google Scholar
Donaldson, C. & Snedeker, R. 1971 A study of free jet impingement. Part 1. Mean properties of free and impinging jets. J. Fluid Mech. 45 (2), 281–319.Google Scholar
Edgington-Mitchell, D., Duke, D., Amili, O., Weightman, J. L., Honnery, D. R. & Soria, J. 2015 Measuring shear layer growth rates in aeroacoustically forced axisymmetric supersonic jets. AIAA Paper 2015–2834.Google Scholar
Edgington-Mitchell, D., Oberleithner, K., Honnery, D. R. & Soria, J. 2014 Coherent structure and sound production in the helical mode of a screeching axisymmetric jet. J. Fluid Mech. 748, 822–847.Google Scholar
Gojon, R. & Bogey, C. 2017 Flow features near plate impinged by ideally expanded and underexpanded round jets. AIAA J. 56, 1–13.Google Scholar
Gojon, R., Bogey, C. & Marsden, O. 2016 Investigation of tone generation in ideally expanded supersonic planar impinging jets using large-eddy simulation. J. Fluid Mech. 808, 90–115.Google Scholar
Henderson, B. 2002 The connection between sound production and jet structure of the supersonic impinging jet. J. Acoust. Soc. Am. 111 (2), 735–747.Google Scholar
Henderson, B., Bridges, J. & Wernet, M. 2005 An experimental study of the oscillatory flow structure of tone-producing supersonic impinging jets. J. Fluid Mech. 542, 115–137.Google Scholar
Henderson, B. & Powell, A. 1993 Experiments concerning tones produced by an axisymmetric choked jet impinging on flat plates. J. Sound Vib. 168 (2), 307–326.Google Scholar
Henderson, L. F. 1966 Experiments on the impingement of a supersonic jet on a flat plate. Z. Angew. Math. Phys. 17 (5), 553–569.Google Scholar
Ho, C. M. & Nosseir, N. S. 1981 Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 105, 119–142.Google Scholar
Krothapalli, A. 1985 Discrete tones generated by an impinging underexpanded rectangular jet. AIAA J. 23 (12), 1910–1915.Google Scholar
Krothapalli, A., Rajkuperan, E., Alvi, F. & Lourenco, L. 1999 Flow field and noise characteristics of a supersonic impinging jet. J. Fluid Mech. 392, 155–181.Google Scholar
Kuo, C. Y. & Dowling, A. P. 1996 Oscillations of a moderately underexpanded choked jet impinging upon a flat plate. J. Fluid Mech. 315, 267–291.Google Scholar
Kweon, Y.-H., Miyazato, Y., Aoki, T., Kim, H.-D. & Setoguchi, T. 2006 Experimental investigation of nozzle exit reflector effect on supersonic jet. Shock Waves 15 (3–4), 229–239.Google Scholar
Manning, T. A. & Lele, S. K.2000 A numerical investigation of sound generation in supersonic jet screech. Tech. Rep. DTIC Document.Google Scholar
Marsh, A. H. 1961 Noise measurements around a subsonic air jet impinging on a plane, rigid surface. J. Acoust. Soc. Am. 33 (8), 1065–1066.Google Scholar
Mason-Smith, N., Edgington-Mitchell, D., Buchmann, N. A., Honnery, D. R. & Soria, J. 2015 Shock structures and instabilities formed in an underexpanded jet impinging on to cylindrical sections. Shock Waves 1–12.Google Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8 (12), 1406.Google Scholar
Meyer, K. E., Pedersen, J. M. & Özcan, O. 2007 A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 583, 199–227.Google Scholar
Mitchell, D. M., Honnery, D. R. & Soria, J. 2012 The visualization of the acoustic feedback loop in impinging underexpanded supersonic jet flows using ultra-high frame rate schlieren. J. Vis. 15 (4), 333–341.Google Scholar
Mitchell, D. M., Honnery, D. R. & Soria, J. 2013 Near-field structure of underexpanded elliptic jets. Exp. Fluids 54 (7), 1–13.Google Scholar
Morris, P. J. 2010 The instability of high speed jets. Intl J. (Wash.) Aeroacoust. 9 (1–2), 1–50.Google Scholar
Nagel, R. T., Denham, J. W. & Papathanasiou, A. G. 1983 Supersonic jet screech tone cancellation. AIAA J. 21 (5), 1541–1545.Google Scholar
Norum, T. D. 1983 Screech suppression in supersonic jets. AIAA J. 21 (2), 235–240.Google Scholar
Nosseir, N. S. & Ho, C. M. 1982 Dynamics of an impinging jet. Part 2. The noise generation. J. Fluid Mech. 116, 379–391.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H. C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.Google Scholar
Poldervaart, L. J., Vink, A. T. & Wijnands, A. P. J. 1968 The photographic evidence of the feedback loop of a two dimensional screeching supersonic jet of air. In Proceedings of the 6th International Congress on Acoustics, Tokyo, Japan.Google Scholar
Ponton, M. K. & Seiner, J. M. 1992 The effects of nozzle exit lip thickness on plume resonance. J. Sound Vib. 154 (3), 531–549.Google Scholar
Powell, A. 1953a On edge tones and associated phenomena. Acta Acust. 3 (4), 233–243.Google Scholar
Powell, A. 1953b On the mechanism of choked jet noise. Proc. Phys. Soc. Lond. B 66 (12), 1039.Google Scholar
Powell, A. 1988 The sound-producing oscillations of round underexpanded jets impinging on normal plates. J. Acoust. Soc. Am. 83 (2), 515–533.Google Scholar
Powell, A., Umeda, Y. & Ishii, R. 1992 Observations of the oscillation modes of choked circular jets. J. Acoust. Soc. Am. 92 (5), 2823–2836.Google Scholar
Raman, G. 1997 Cessation of screech in underexpanded jets. J. Fluid Mech. 336, 69–90.Google Scholar
Raman, G., Panda, J., Zaman, K. B. M. Q., Raman, G., Panda, J. & Zaman, K. 1997 Feedback and receptivity during jet screech-influence of an upstream reflector. In 35th Aerospace Sciences Meeting and Exhibit, p. 144.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part i: coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12 (2), 221–233.Google Scholar
Stegeman, P. C., Pérez, J. M., Soria, J. & Theofilis, V. 2016 Inception and evolution of coherent structures in under-expanded supersonic jets. J. Phys.: Conf. Ser. 708, 012015.Google Scholar
Tam, C. K. W. & Ahuja, K. K. 1990 Theoretical model of discrete tone generation by impinging jets. J. Fluid Mech. 214, 67–87.Google Scholar
Tam, C. K. W. & Norum, T. 1992 Impingement tones of large aspect ratio supersonic rectangular jets. AIAA J. 30 (2), 304–311.Google Scholar
Tan, D. J., Soria, J., Honnery, D. & Edgington-Mitchell, D. 2017 Novel method for investigating broadband velocity fluctuations in axisymmetric screeching jets. AIAA J 55, 2321–2334.Google Scholar
Thurow, B., Samimy, M. & Lempert, W. 2002 Structure of a supersonic impinging rectangular jet via real-time optical diagnostics. AIAA Paper 2002–2865.Google Scholar
Vinoth, B. R., Throvagunta, P. & Rathakrishnan, E. 2011 Effect of upstream reflector on jet screech. AIAA J. 49 (6), 1151–1157.Google Scholar
Weightman, J. L., Amili, O., Honnery, D., Edgington-Mitchell, D. M. & Soria, J. 2017a On the effects of nozzle lip thickness on the azimuthal mode selection of a supersonic impinging flow. In 23rd AIAA/CEAS Aeroacoustics Conf, p. 3031.Google Scholar
Weightman, J. L., Amili, O., Honnery, D., Soria, J. & Edgington-Mitchell, D. 2017b An explanation for the phase lag in supersonic jet impingement. J. Fluid Mech. 815.Google Scholar

Weightman et al. supplementary movie

Ultra high-speed schlieren of the sound generation at the standoff shock. The jet was emanating from the infinite-lip nozzle, at an NPR of 3.4 and z/D of 5.0.

Download Weightman et al. supplementary movie(Video)
Video 8.4 MB