Article contents
A note on the stability of inviscid zonal jet flows on a rotating sphere
Published online by Cambridge University Press: 06 September 2012
Abstract
The linear stability of inviscid zonal jet flows on a rotating sphere is re-examined. A semi-circle theorem for inviscid zonal flows on a rotating sphere is proved. It is also shown that numerically obtained eigenvalues of the linear stability problem do not converge well with a spectral method which was adopted in previous studies, due to an emergence of critical layers near the poles. By using a shooting method where the integral path bypasses the critical layers in the complex plane, the eigenvalues are successfully obtained with 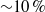 correction of the critical rotation rates compared to those obtained in Baines (J. Fluid Mech., vol. 73, 1976, pp. 193–213).
correction of the critical rotation rates compared to those obtained in Baines (J. Fluid Mech., vol. 73, 1976, pp. 193–213).
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 8
- Cited by


