Article contents
Non-steady columnar motions in rotating stratified Boussinesq fluids: exact Lagrangian and Eulerian description
Published online by Cambridge University Press: 05 December 2011
Abstract
This paper aims to narrow the gap between the Lagrangian and Eulerian descriptions of rotating stratified fluids. To this end, without loss of generality the primitive Lagrangian equations with arbitrary oriented time-dependent rotation 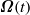 and arbitrary stable stratification have been simplified and made more amenable for analysis. The bulk of the work is concerned with developing in parallel exact Lagrangian and Eulerian descriptions of a particular interesting class of motions of rotating stratified incompressible Boussinesq fluids: the vertically uniform columnar motions. The Lagrangian description is confined to ideal fluids, while the Eulerian one includes viscosity and diffusivity. Assuming the rotation axis to be parallel to gravity, with the rotation rate being an arbitrary function of time, and the buoyancy frequency to be constant, it is found that for vertically uniform motions there is always an exact split into horizontal and vertical subsystems. Evolution of the horizontal velocities and displacements is governed by the classical equations of two-dimensional incompressible hydrodynamics, only slightly modified by accounting for the variable rotation rate. These equations are independent of stratification and vertical motions. The Coriolis term is potential and can be incorporated into pressure. The vertical motions represent a manifestation of packets of inertia–gravity waves with strictly horizontal wavevectors, and are exactly described by linear equations independently of the wave amplitudes. They do not depend on rotation, either constant or variable. The wavepackets do not interact with each other or with horizontal motions. For ideal fluids or those with Rayleigh friction there are explicit solutions describing these motions for arbitrary initial conditions. The Cauchy problem for the columnar motions in ideal fluids is found to be well posed. Thus there is a natural extension of well-studied two-dimensional incompressible hydrodynamics which retains the property of the absence of vortex stretching: all two-dimensional flows could be ‘dressed up’ by adding appropriate vertical motions of a rotating stratified fluid. All the columnar motions could be described in such a way. The examined columnar motions exist under arbitrary relations between the parameters of rotation and stratification and, in particular, without rotation. In the limit of strong rotation one recovers the results known in the literature, in particular, under additional assumptions of small amplitude and steadiness of motions the solutions describe the classical Taylor–Proudman columns.
and arbitrary stable stratification have been simplified and made more amenable for analysis. The bulk of the work is concerned with developing in parallel exact Lagrangian and Eulerian descriptions of a particular interesting class of motions of rotating stratified incompressible Boussinesq fluids: the vertically uniform columnar motions. The Lagrangian description is confined to ideal fluids, while the Eulerian one includes viscosity and diffusivity. Assuming the rotation axis to be parallel to gravity, with the rotation rate being an arbitrary function of time, and the buoyancy frequency to be constant, it is found that for vertically uniform motions there is always an exact split into horizontal and vertical subsystems. Evolution of the horizontal velocities and displacements is governed by the classical equations of two-dimensional incompressible hydrodynamics, only slightly modified by accounting for the variable rotation rate. These equations are independent of stratification and vertical motions. The Coriolis term is potential and can be incorporated into pressure. The vertical motions represent a manifestation of packets of inertia–gravity waves with strictly horizontal wavevectors, and are exactly described by linear equations independently of the wave amplitudes. They do not depend on rotation, either constant or variable. The wavepackets do not interact with each other or with horizontal motions. For ideal fluids or those with Rayleigh friction there are explicit solutions describing these motions for arbitrary initial conditions. The Cauchy problem for the columnar motions in ideal fluids is found to be well posed. Thus there is a natural extension of well-studied two-dimensional incompressible hydrodynamics which retains the property of the absence of vortex stretching: all two-dimensional flows could be ‘dressed up’ by adding appropriate vertical motions of a rotating stratified fluid. All the columnar motions could be described in such a way. The examined columnar motions exist under arbitrary relations between the parameters of rotation and stratification and, in particular, without rotation. In the limit of strong rotation one recovers the results known in the literature, in particular, under additional assumptions of small amplitude and steadiness of motions the solutions describe the classical Taylor–Proudman columns.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 2
- Cited by


