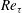Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T15:09:40.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-periodic phase-space trajectories of roughness-driven secondary flows in high-$Re_{\unicode[STIX]{x1D70F}}$ boundary layers and channels

Published online by Cambridge University Press:  18 April 2019

W. Anderson Open the ORCID record for W. Anderson [Opens in a new window]
W. Anderson*
Affiliation:
Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, Texas, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent flows respond to bounding walls with a predominant spanwise heterogeneity – that is, a heterogeneity parallel to the prevailing transport direction – with formation of Reynolds-averaged turbulent secondary flows. Prior experimental and numerical work has determined that these secondary rolls occur in a variety of arrangements, contingent only upon the existence of a spanwise heterogeneity (i.e. from complex, multiscale roughness with a predominant spanwise heterogeneity, to canonical step changes, to different roughness elements). These secondary rolls are known to be a manifestation of Prandtl’s secondary flow of the second kind: driven and sustained by the existence of spatial heterogeneities in the Reynolds (turbulent) stresses, all of which vanish in the absence of spanwise heterogeneity. Herein, we show results from a suite of large-eddy simulations and complementary experimental measurements of flow over spanwise-heterogeneous surfaces. Although the resultant secondary cell location is clearly correlated with the surface characteristics, which ultimately dictates the Reynolds-averaged flow patterns, we show the potential for instantaneous sign reversals in the rotational sense of the secondary cells. This is accomplished with probability density functions and conditional sampling. In order to address this further, a base flow representing the streamwise rolls is introduced. The base flow intensity – based on a leading-order Galerkin projection – is allowed to vary in time through the introduction of time-dependent parameters. Upon substitution of the base flow into the streamwise momentum and streamwise vorticity transport equations, and via use of a vortex forcing model, we are able to assess the phase-space evolution (orbit) of the resulting system of ordinary differential equations. The system resembles the Lorenz system, but the forcing conditions differ intrinsically. Nevertheless, the system reveals that chaotic, non-periodic trajectories are possible for sufficient inertial conditions. Poincaré projection is used to assess the conditions needed for chaos, and to estimate the fractal dimension of the attractor. Its simplicity notwithstanding, the propensity for chaotic, non-periodic trajectories in the base flow model suggests similar dynamics is responsible for the large-scale reversals observed in the numerical and experimental datasets.

JFM classification

Boundary Layers: Boundary layer structure Nonlinear Dynamical Systems: Chaos
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 869 , 25 June 2019 , pp. 27 - 84
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1988 Linking correlations and structure: stochastic estimation and conditional averaging. In Zoran P. Zaric Memorial International Seminar on Near-Wall Turbulence. Hemisphere.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Anderson, W. 2012 An immersed boundary method wall model for high-Reynolds number channel flow over complex topography. Intl J. Numer. Meth. Fluids 71, 1588–1608.Google Scholar
Anderson, W., Barros, J. M., Christensen, K. T. & Awasthi, A. 2015 Numerical and experimental study of mechanisms responsible for turbulent secondary flows in boundary layer flows over spanwise heterogeneous roughness. J. Fluid Mech. 768, 316–347.Google Scholar
Anderson, W. & Meneveau, C. 2010 A large-eddy simulation model for boundary-layer flow over surfaces with horizontally resolved but vertically unresolved roughness elements. Boundary-Layer Meteorol. 137, 397–415.Google Scholar
Anderson, W., Yang, J., Shrestha, K. & Awasthi, A. 2018 Turbulent secondary flows in wall turbulence: vortex forcing, scaling arguments, and similarity solution. Env. Fluid Mech. 18, 1351–1378.Google Scholar
Antonia, R. A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13, 131–156.Google Scholar
Antonia, R. A. & Luxton, R. E. 1971 The response of a turbulent boundary layer to a step change in surface roughness. Part I. Smooth to rough. J. Fluid Mech. 48, 721–761.Google Scholar
Awasthi, A. & Anderson, W. 2018 Numerical study of turbulent channel flow perturbed by spanwise topographic heterogeneity: amplitude and frequency modulation within low-and high-momentum pathways. Phys. Rev. Fluids 3, 044602.Google Scholar
Baars, W. J., Talluru, M. K., Hutchins, N. & Marusic, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scales. Exp. Fluids 56, 188–1–15.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Barros, J. M. & Christensen, K. T. 2014 Observations of turbulent secondary flows in a rough-wall boundary layer. J. Fluid Mech. 748, R1.Google Scholar
Belcher, S. E., Harman, I. N. & Finnigan, J. J. 2012 The wind in the willows: flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 44, 479–504.Google Scholar
Bons, J. P., Taylor, R. P., McClain, S. T. & Rivir, R. B. 2001 The many faces of turbine surface roughness. J. Turbomach. 123, 739–748.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2004 Large-eddy simulation of neutral atmospheric boundary layer flow over heterogeneous surfaces: blending height and effective surface roughness. Water Resour. Res. 40, W02505.Google Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.Google Scholar
Bouchet, F. & Barré, J. 2005 Classification of phase transitions and ensemble inequivalence, in systems with long range interactions. J. Stat. Phys. 118, 1073–1105.Google Scholar
Bouchet, F. & Simonnet, E. 2009 Random changes of flow topology in two-dimensional and geophysical turbulence. Phys. Rev. Lett. 102, 094504.Google Scholar
Bouchet, F. & Venaille, A. 2012 Statistical mechanics of two-dimensional and geophysical flows. Phys. Rep. 515, 227–295.Google Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.Google Scholar
Brundrett, E. & Baines, W. D. 1964 The production and diffusion of vorticity in duct flow. J. Fluid Mech. 19, 375–394.Google Scholar
Brunton, S. L., Proctor, J. L. & Kutz, J. N. 2016 Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113, 3932–3937.Google Scholar
Castro, I. P. 2007 Rough-wall boundary layers: mean flow universality. J. Fluid Mech. 585, 469–485.Google Scholar
Chester, S., Meneveau, C. & Parlange, M. B. 2007 Modelling of turbulent flow over fractal trees with renormalized numerical simulation. J. Comput. Phys. 225, 427–448.Google Scholar
Chung, D., Monty, J. P. & Hutchins, N. 2018 Similarity and structure of wall turbulence with lateral wall shear stress variations. J. Fluid Mech. 847, 591–613.Google Scholar
Craik, A. D. D. 1985 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Farmer, J. D., Ott, E. & Yorke, J. A. 1983 The dimension of chaotic attractors. Physica D 7, 153–180.Google Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.Google Scholar
Fishpool, G. M., Lardeau, S. & Leschziner, M. A. 2009 Persistent non-homogeneous features in periodic channel-flow simulations. Flow Turbul. Combust. 83, 323–342.Google Scholar
Flack, K. A. & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. J. Fluids Engng 132 (4), 041203.Google Scholar
Flack, K. A., Schultz, M. P. & Connelly, J. S. 2007 Examination of a critical roughness height for outer layer similarity. Phys. Fluids 19 (9), 095104.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Garratt, J. R. 1990 The internal boundary layer – a review. Boundary-Layer Meteorol. 40, 171–203.Google Scholar
Gayme, D. F., McKeon, B. J., Papachristodoulou, A., Bamieh, B. & Doyle, J. C. 2010 A streamwise constant model of turbulence in plane Couette flow. J. Fluid Mech. 665, 99–119.Google Scholar
Gessner, F. B. 1973 The origin of secondary flow in turbulent flow along a corner. J. Fluid Mech. 58, 1–25.Google Scholar
Goldstein, D. B. & Tuan, T.-C. 1998 Secondary flow induced by riblets. J. Fluid Mech. 363, 115–151.Google Scholar
Graham, J. & Meneveau, C. 2012 Modeling turbulent flow over fractal trees using renormalized numerical simulation: alternate formulations and numerical experiments. Phys. Fluids 24, 125105.Google Scholar
Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50, 233–255.Google Scholar
Grassberger, P. & Procaceia, I. 1983 Characterization of strange attractors. Phys. Rev. Lett. 50, 346–349.Google Scholar
Hinze, J. O. 1967 Secondary currents in wall turbulence. Phys. Fluids (Suppl.) 10, S122–S125.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry, Cambridge Monographs on Mechanics. Cambridge University Press.Google Scholar
Hong, J., Katz, J., Meneveau, C. & Schultz, M. 2012 Coherent structures and associated subgrid-scale energy transfer in a rough-wall channel flow. J. Fluid Mech. 712, 92–128.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Jacob, C. & Anderson, W. 2016 Conditionally averaged large-scale motions in the neutral atmospheric boundary layer: insights for aeolian processes. Boundary-Layer Meteorol. 162, 21–41.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26, 095102.Google Scholar
Jimenez, J. 2004 Turbulent flow over rough wall. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Kevin, Monty, J. P., Bai, H. L., Pathikonda, G., Nugroho, B., Barros, J. M., Christensen, K. T. & Hutchins, N. 2017 Cross-stream stereoscopic particle image velocimetry of a modified turbulent boundary layer over directional surface pattern. J. Fluid Mech. 813, 412–435.Google Scholar
Kevin, Monty, J. & Hutchins, N. 2019 Turbulent structures in a statistically three-dimensional boundary layer. J. Fluid Mech. 859, 543–565.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully-developed channel flow at low Reynolds-number. J. Fluid Mech. 177, 133–166.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11, 417–422.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41 (02), 283–325.Google Scholar
Krogstad, P. Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Laufer, J.1954 The structure of turbulence in fully developed pipe flow. NACA Tech. Rep. 1174.Google Scholar
Laurie, J. & Bouchet, F. 2015 Computation of rare transitions in the barotropic quasi-geostrophic equations. New J. Phys. 17, 015009.Google Scholar
Lee, J., Jelly, T. O. & Zaki, T. A. 2015 Effect of Reynolds number on turbulent drag reduction by superhydrophobic surface textures. Flow Turbul. Combust. 95, 1–24.Google Scholar
Leibovich, S. 1977 Convective instability of stably stratified water in the ocean. J. Fluid Mech. 82, 561–585.Google Scholar
Leibovich, S. 1980 On wave-current interaction theories of langmuir circulations. J. Fluid Mech. 99, 715–724.Google Scholar
Leibovich, S. 1983 The form and dynamics of langmuir circulation. Annu. Rev. Fluid Mech. 15, 391–427.Google Scholar
Lorenz, E. N. 1963 Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141.Google Scholar
Lundquist, K. A., Chow, F. K. & Lundquist, J. K. 2010 An immersed boundary method for the weather research and forecasting model. Mon. Weath. Rev. 138, 796–817.Google Scholar
Mansfield, J. R., Knio, O. M. & Meneveau, C. 1998 A dynamic les scheme for the vorticity transport equation: formulation and a priori tests. J. Comput. Phys. 145, 693–730.Google Scholar
Mansfield, J. R., Knio, O. M. & Meneveau, C. 1999 Dynamic les of colliding vortex rings using a 3d vortex method. J. Comput. Phys. 152, 305–345.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.Google Scholar
McWilliams, J. C., Sullivan, P. P. & Moeng, C.-H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.Google Scholar
Medjnoun, T., Vanderwel, C. & Ganapathisubramani, B. 2018 Characteristics of turbulent boundary layers over smooth surfaces with spanwise heterogeneities. J. Fluid Mech. 838, 516–543.Google Scholar
Mejia-Alvarez, R., Barros, J. M. & Christensen, K. T. 2013 Structural attributes of turbulent flow over a complex topography. In Coherent Flow Structures at the Earth’s Surface (ed. Venditti, J. G., Best, J. L., Church, M. & Hardy, R. J.), chap. 3, pp. 25–42. Wiley-Blackwell.Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2010 Low-order representations of irregular surface roughness and their impact on a turbulent boundary layer. Phys. Fluids 22, 015106.Google Scholar
Mejia-Alvarez, R. & Christensen, K. T. 2013 Wall-parallel stereo PIV measurements in the roughness sublayer of turbulent flow overlying highly-irregular roughness. Phys. Fluids 25, 115109.Google Scholar
Meyers, J., Ganapathisubramani, B. & Cal, R. B. 2019 On the decay of dispersive motions in the outer region of rough-wall boundary layers. J. Fluid Mech. 862, R5.Google Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.Google Scholar
Nezu, I. & Nakagawa, H. 1993 Turbulence in Open-Channel Flows. Balkema Publishers.Google Scholar
Nugroho, B., Hutchins, N. & Monty, J. P. 2013 Large-scale spanwise periodicity in a turbulent boundary layer induced by highly ordered and direction surface roughness. Intl J. Heat Fluid Flow 41, 90–102.Google Scholar
Orszag, S. A. 1970 Transform method for calculation of vector coupled sums: application to the spectral form of the vorticity equation. J. Atmos. Sci. 27, 890–895.Google Scholar
Ott, E. 2002 Chaos in Dynamical Systems. Cambridge University Press.Google Scholar
Pathikonda, G. & Christensen, K. T. 2017 Inner–outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2, 044603.Google Scholar
Peitgen, H.-O., Jürgens, H. & Saupe, D. 1992 Chaos and Fractals. Springer.Google Scholar
Perkins, H. J. 1970 The formation of streamwise vorticity in turbulent flow. J. Fluid Mech. 44, 721–740.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Prandtl, L. 1952 Essentials of Fluid Dynamics. Blackie and Son.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.Google Scholar
Reynolds, R. T., Hayden, P., Castro, I. P. & Robins, A. G. 2007 Spanwise variations in nominally two-dimensional rough-wall boundary layers. Exp. Fluids 42, 311–320.Google Scholar
Richter, D. H. & Sullivan, P. P. 2014 Modification of near-wall coherent structures by inertial particles. Phys. Fluids 26, 103304.Google Scholar
Saltzman, B. 1962 Finite amplitude free convection as an initial value problem – I. J. Atmos. Sci. 19, 329–341.Google Scholar
Schultz, M. P. 2007 Effects of coating roughness and biofouling on ship resistance and powering. Biofouling 23, 331–341.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21 (1), 015104.Google Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.Google Scholar
de Silva, C. M., Kevin, Baidya, R., Hutchins, N. & Marusic, I. 2018 Large coherence of spanwise velocity in turbulent boundary layers. J. Fluid Mech. 847, 161–185.Google Scholar
Smagorinsky, J. S. 1963 General circulation experiments with the primitive equations. Mon. Weath. Rev. 91, 99–164.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–455.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vanderwel, C. & Ganapathisubramani, B. 2015 Effects of spanwise spacing on large-scale secondary flows in rough-wall turbulent boundary layers. J. Fluid Mech. 774, R2.Google Scholar
Vanderwel, C., Stroh, A., Kriegseis, J., Frohnapfel, B. & Ganapathisubramani, B. 2019 The instantaneous structure of secondary flows in turbulent boundary layers. J. Fluid Mech. 862, 845–870.Google Scholar
Vermaas, D. A., Uijttewall, W. S. J. & Hoitink, A. J. F. 2011 Lateral transfer of streamwise momentum caused by a roughness transition across a shallow channel. Water Resour. Res. 47, W02530.Google Scholar
Volino, R. J., Schultz, M. P. & Flack, K. A. 2007 Turbulence structure in rough- and smooth-wall boundary layers. J. Fluid Mech. 592, 263–293.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wang, Z.-Q. & Cheng, N.-S. 2005 Secondary flows over artificial bed strips. Adv. Water Resour. 28, 441–450.Google Scholar
Willingham, D., Anderson, W., Christensen, K. T. & Barros, J. 2013 Turbulent boundary layer flow over transverse aerodynamic roughness transitions: induced mixing and flow characterization. Phys. Fluids 26, 025111.Google Scholar
Wood, D. H.1981 The growth of the internal layer following a step change in surface roughness. Report T.N. – FM 57, Dept. of Mech. Eng., University of Newcastle, Australia.Google Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.Google Scholar
Wu, Y. & Christensen, K. T. 2007 Outer-layer similarity in the presence of a practical rough-wall topology. Phys. Fluids 19, 085108.Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar
Yang, D., Chen, B., Chamecki, M. & Meneveau, C. 2015 Oil plumes and dispersion in Langmuir, upper-ocean turbulence: large-eddy simulations and k-profile parameterization. J. Geophys. Res.: Oceans 120, 4729–4759.Google Scholar
Yang, J. & Anderson, W. 2017 Turbulent channel flow over surfaces with variable spanwise heterogeneity: establishing conditions for outer-layer similarity. Flow Turbul. Combust. 100, 1–17.Google Scholar